尾缘柔性变形对翼型水动力学性能的影响❋

张敬斌， 王树杰,2❋❋， 袁 鹏,2， 谭俊哲,2， 司先才,2

(1.中国海洋大学工程学院，山东 青岛 266100； 2. 青岛市海洋可再生能源重点实验室，山东 青岛 266100)

海洋能作为一种新型可再生能源，其开发和利用越来越受关注[1]。叶片是潮流能水轮机重要组成部分，翼型对水轮机叶片水动力学性能有着重要影响[2]。目前潮流能水轮机叶片大多采用刚性叶片，为适应复杂海洋环境，研究使用柔性材料制作的叶片应用到潮流能发电中[3]。柔性叶片在流体作用下，会产生自适应变形，可以减少作用在叶片上的负载，同时由于叶片与流体的相互耦合作用，会引起流场的变化，使柔性叶片水轮机的水动力学性能与刚性叶片水轮机存在差异[4-6]。自适应柔性叶水轮机具有低速启动、中速恒压等优点，而在微观层面上，柔性叶片的变形会引起翼型形状变化，改变了叶片整体水动力学性能。

在风力发电机和航天飞行器上，研究者针对翼型变形问题进行了诸多研究，卢天宇等[7]应用小尺寸机翼前缘动态变形(DDLE)技术，通过改变前缘形状，改善翼型前缘区域的速度梯度，抑制动态失速效应。徐国武等[8]对飞行器的翼型进行分析，数值模拟了儒可夫斯基翼型连续改变厚度、弯度所引起的气动特性变化，分析了不同变形幅度、变形速度以及变形加速度对非定常升力系数的影响情况，为以后的三维数值模拟提供了基础。郭秋亭等[9]对变形过程中的非定常分离流动进行了数值模拟，分析了各种变形参数对流动分离的影响，最终得到，局部主动变形可以改善翼型的升阻力的特性的结论。叶舟等[10]对柔性翼型的主动控制和气动特性进行研究，讨论变形对翼型的升阻力特性的影响，同时对翼型周围流场进行分析。

潮流能水轮机叶片的研究方法与风机叶片和机翼研究方法基本是一致的。以NACA4415翼型为研究对象，借助ANSYS对翼型所在平面进行静力学分析，确定变形节点参数，最后将变形后的翼型通过CFD软件仿真分析，研究自适应变形对翼型升阻力特性及流场的影响。

1 柔性叶片模型

潮流能水轮机柔性叶片在建模过程中，通常会采取增加弦长、自适应翼型尾缘和自适应叶片扭角等方法[11]。为降低建模难度，采取自适应翼型尾缘的建模方法，以NACA4415翼型为基础翼型，建立柔性叶片三维模型，叶片长度300 mm(见图1)。图中白色部分为刚性材料，在流体中不发生形变，黑色部分为柔性弹性材料，定义其弹性模量为0.5 MPa，泊松比为0.3，叶片以弦长的11/20D处为分界线。

图1 柔性叶片模型Fig.1 Flexible blade model

将上述模型，作为研究柔性叶片变形对潮流能水轮机水动力学性能影响的对象。宏观上，柔性叶片发生弦向形变；微观上，翼型尾缘发生形变，使叶片水动力学性能发生改变。

在静力学仿真实验中，选取叶片截面进行研究，翼型弦长为30 mm。研究表明，翼型自适应变形方向总沿y轴的正方向，见图2，在ANSYS中对翼型平面进行静力学分析，在施加沿y轴正方向作用力后，可获得其变形量。

2 数值计算过程

2.1 翼型平面静力学分析

在ANSYS中对翼型平面进行材料属性定义，由于作用力沿y轴方向，其在y方向上发生大形变，在x轴方向形变较小，见图2。

图2 叶片截面的变形示意Fig.2 Schematic section of blade deformation

(1)

(2)

(3)

对于由若干微元组成的翼型平面而言，在求出每个微元的单元刚度矩阵后，通过叠加可以求出整体的刚度矩阵。对翼型平面进行静力分析，其总的等效方程为：

Kμ=FaFr，

(4)

(5)

其中：[K]为总刚度矩阵；[μ]为节点位移矢量；[Fa]为所受总外载荷；[Fr]为支反载荷矢量；[Kε]为单元刚度矩阵；N为单元数。

根据位移插值函数以及弹性力学中给出的应变和位移及应变和应力关系，求出各个节点位移参数。

在静力学分析时，翼型处在0°攻角下，以y轴方向最大变形作为参考值，施加不同作用力后，翼型变形量见表1。再通过数据处理后，得出变形后翼型曲线，见图3。

图3 变形后的翼型曲线Fig.3 The airfoil curve after deformation

表1 最大变形量Table 1 Maximum deformation

2.2 几何模型及网格划分

利用前处理软件Gambit进行翼型几何模型的建立，同时对翼型的二维计算域和网格进行处理。原始翼型的弦长为0.030 m，考虑到流动的充分发展和计算的收敛性，计算域是由一个直径为20倍弦长的半圆形和一个长宽均为20倍弦长的正方形构成，翼型位于半圆的中心位置。计算网格采用非结构性网格，网格的数量在5.5万左右，鉴于翼型附近的流动较为复杂，所以对翼型周围进行加密处理(见图4)。

图4 翼型计算域及网格Fig.4 Airfoil computational domain and grid

2.3 Fluent中数值分析过程

借助Fluent对翼型进行数值模拟，翼型所处的流场为二维黏性不可压缩的流场，其控制方程由连续性方程和动量方程组成。

动量方程为：

(6)

动量方程为：

(7)

(8)

其中：Re为雷诺数；μ为动力黏度系数；u，v为x，y方向的速度分量，m·s-1；P为流体压力，Pa。

在进行Fluent模拟时，选取适当的湍流模型很重要，二方程湍流模型由于有很好的计算精度同时又容易收敛而被广泛使用。此次翼型分析选择k-ωSST模型[12]，其模型基于梯度扩散假设，建立起了平均速度场梯度、湍流粘度和雷诺应力之间的关系，同时湍流粘度是湍流长度尺寸与湍流速度的乘积，对于k-ω模型，其有一个优点就是在进行低雷诺数计算时对近壁面的处理。该模型没有像k-ε模型要求复杂的非线性阻尼功能，因此其更精确、更稳健[13]。

动量、湍流动能均采用二阶迎风格式的离散方法，压力-速度耦合使用SIMPLE算法。其中圆弧区域为速度进口边界条件(Velocity-inlet)，右侧为压力出口边界条件(Pressure-outlet)，翼型表面及上下边线为固壁边界条件(Wall)。其中湍流强度设置为5%，雷诺数为Re=1.4×105。

3 原始翼型的升阻力特性分析

对原始翼型NACA4415进行水动力学性能的数值模拟，获得升力系数、阻力系数和升阻比随攻角的变化曲线(见图5)。

图5 原始翼型数值模拟仿真值Fig.5 Numerical simulation of the original airfoil

由图可以看出，原始NACA4415翼型在9°之前随着攻角的增加，其升力系数、阻力系数逐渐增加，且阻力系数增速较缓，在攻角为9°时，升力系数达到最大值，当攻角大于9°时，由于失速现象的产生，其升力系数迅速降低，阻力系数随之迅速增加，翼型的水动力学性能下降，即失速角在9°左右。该翼型的升阻比在6°达到最大值，即20左右，当超过6°时升阻比开始下降。

在攻角为6°时翼型的后缘附近有较小范围的分离涡脱落，对翼型的升阻力系数没有影响，在攻角为9°时，开始出现涡脱现象，升力系数达到最大值。当攻角为12°时，翼型上表面出现大面积的分离涡，升力系数迅速下降，阻力系数迅速上升，翼型存在失速现象。

通过分析原始翼型的水动力学性能，获得该翼型的升阻力特性，与变形后翼型进行对比分析。

4 变形后翼型的水动力学对比分析

4.1 变形对升阻力系数的影响

首先通过对攻角为0°的NACA4415翼型不同变形情况下的仿真模拟，获得其变形后翼型的升阻力系数变化曲线见图6(a)，其升阻比变化曲线见图6(b)。

当变形量沿着y轴正方向增加时，升力系数增幅呈先增大后减小的趋势，阻力系数呈现不断增加的趋势。当变形量为0.90 mm时，其升力系数增长率约为80%，阻力系数增长率约2%，升阻比增长率约为80%；当变形量为2.7 mm时，其升力系数的增长率约为236%，阻力系数的增长率约为47%，同时其升阻比达到最大值，增长率约为128%；当变形量为3.5 mm时，升力系数达到最大，其增长率为281%；当变形量为5.1 mm时，其升力系数增长率达到220%左右，而其阻力系数增长率约为297%，升阻比的增长率约为-18%。

图6 变形后的翼型升阻力变化曲线Fig.6 Change curve of lift drag and coefficient after deformation

为进一步研究变形对翼型水动力学性能的影响，选取三组不同的变形量，分别为2.7、3.5和5.1 mm，分析在不同攻角下变形后翼型的水动力学性能，与原始翼型进行对比，结果见图7。

当变形沿着y轴正方向增加时，在不同攻角下，翼型的升力系数会稳定在一定范围，其阻力系数会随着攻角增加而迅速增加，见图7(a、b)。在变形从2.7～5.1 mm的过程中，翼型的升力系数大于原始翼型的升力系数；其阻力系数随着攻角的增加，增加幅度也大于原始翼型。

在升阻比图中，在变形为2.7及3.5 mm时，当攻角为-5°～5°左右时，变形后翼型的升阻比大于未变形翼型的升阻比；当攻角为5°～12°时，变形后翼型的升阻比小于原始翼型。当变形为5.1 mm时，当攻角为-5°～2°左右时，其升阻比大于未变形翼型，当攻角为2°～12°时，其升阻比小于未变形翼型。

图7 原始与变形后翼型的升阻力特性分析Fig.7 The analysis of the rise and drag characteristics of the original and deformed hydrofoil

经过分析可得，在不同变形量下，变形后翼型具有相同变化规律。当变形沿着y正方向时，其升力系数会大于原始翼型，且会稳定在一定范围，同时变形后翼型在某些攻角下升阻比大于原始翼型，其性能会比原始翼型更优。

4.2 变形后翼型水动力学性能分析

为研究尾缘变形对翼型的水动力学性能影响的原因，选取部分变形后翼型的翼型表面压力系数，与原始翼型的表面压力系数进行对比，结果见图8。

由图8可得，当变形的方向沿y轴正方向时，与原始翼型相比，压力面的压力系数增大，吸力面的系数减小，上下翼型表面的压差增大，压力系数分布曲线包围的面积增加，使得升力系数增加。

进一步分析可得，当翼型沿着y正方向变形量增加时，其翼型压力系数曲线所包围面积变化幅度不明显，这就验证了沿y正方向变形对翼型的升力系数的影响规律，见图7(a)，变形后翼型升力系数会稳定在一定的范围内。

当攻角为9°时，原始翼型的升力系数达到最大值，其压力曲线包围的面积达到最大值，但其包围的面积仍小于变形为2.7 mm攻角为9°的变形后翼型(见图8e、f)。

这些压力曲线所包围面积的变化，说明了变形后翼型升力系数随变形及攻角变化的原因。

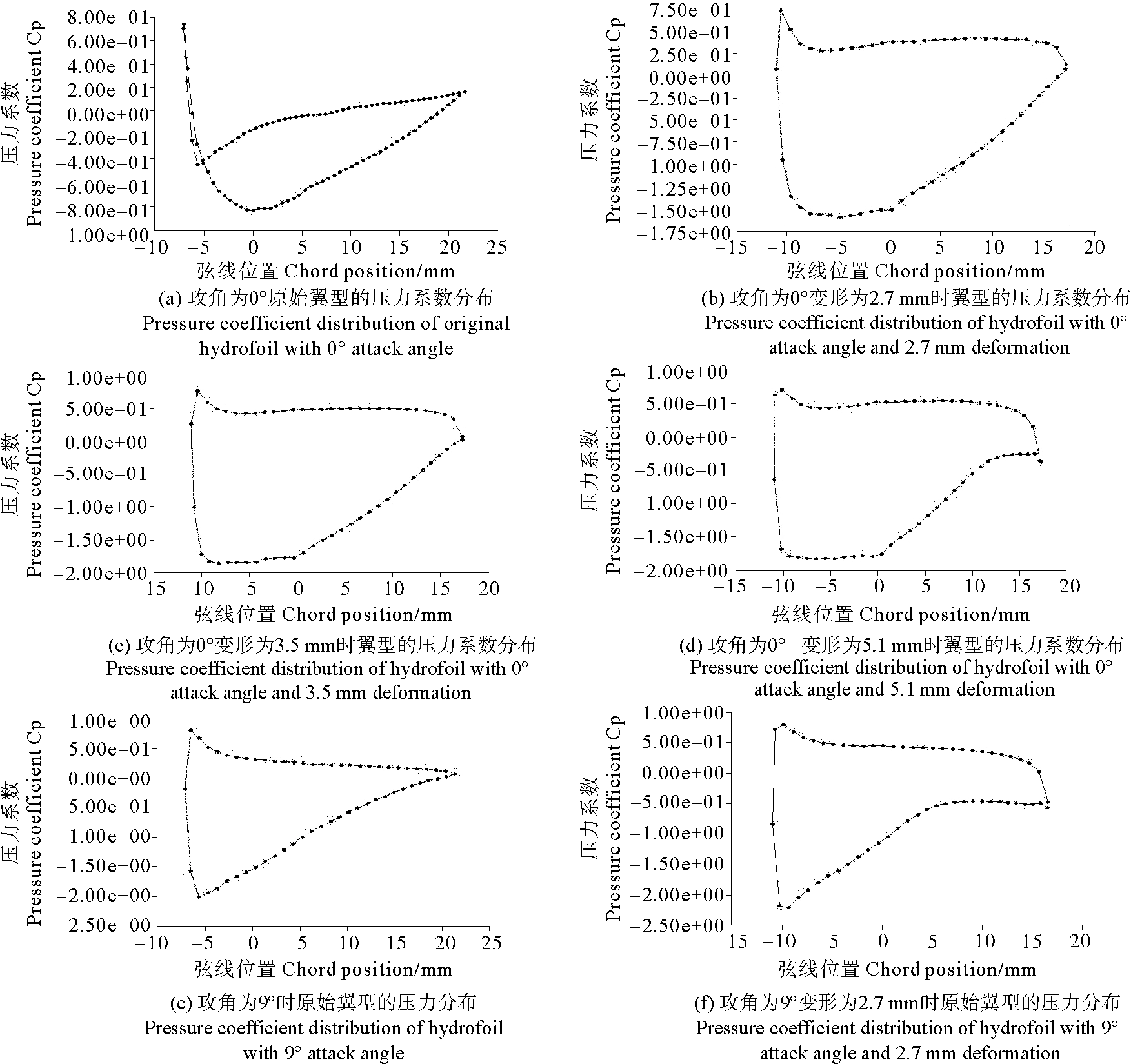
图8 压力系数分布曲线Fig.8 The distribution of pressure coefficient

为进一步分析翼型的水动力学性能，选定攻角为9°时，变形后翼型与原始翼型尾缘附近流场的变化情况(见图9)。

由于变形增加了翼型尾缘的曲率，导致翼型上表面尾缘附近的流线向下弯曲，增加了翼型的环量，使升力增加。但变形使得流动分离更加的明显，从图中可以看出，随着变形的增加，尾缘附近的分离涡越来越明显，且数量也在增加，使得阻力增加，即阻力系数也随之迅速增加。变形后翼型的升阻比，在一定攻角下，会小于原始翼型。以上的分析解释了变形后翼型的升阻力系数及升阻比的变化规律及其原因。

叶片升力相对旋转轴产生扭矩推动水轮机转动，翼型的柔性变形一定情况下可以提高翼型的升力，根据叶素动量理论(BEM)，变形后的叶片所受升力同样会相应提高。与刚性叶片对比，在流体在作用下，柔性叶片变形，提高了转子扭矩，即使在较低的流速下柔性叶片水轮机也可正常工作。同时柔性叶片的使用可以降低叶片的疲劳载荷[14]。

图9 翼型尾缘附近流线Fig.6 Streamline near the trailing edge of the airfoil

5 结论

通过对变形后翼型的水动力学性能分析，得到以下结论：

(1) 当变形方向沿着y正方向时，在一定变形范围内，其升力系数、阻力系数都增加；在不同的攻角下，变形翼型的升力系数大于原始翼型，即尾缘的局部变形对提高翼型的升力具有明显的效果，解释了柔性叶片可以在低流速启动的原因。

(2) 变形对翼型的升阻比产生较大影响，当变形沿着y正方向时，其升阻比在较小攻角下大于原始翼型；随着攻角增加，变形翼型的升阻比小于原始翼型，即在小攻角下，局部变形可以改善翼型的水动力学性能。

本文对柔性尾缘翼型进行了变形后的定性分析，得到了其对翼型水动力学性能的影响规律，为后续潮流能柔性叶片水轮机水动力学性能的研究奠定了基础。