在错题中淘“金”
葛亚美
同学们若能从所做的错题中得到启发,相信你的成绩会有较大的提高。下面是“展开与折叠”这一节中容易做错的一些题目,让我们一起来看看。
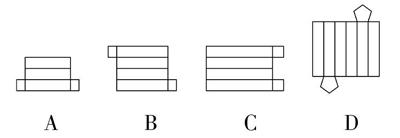
例1 下列图形中能折叠成棱柱的是()。
A B C D
【错解】A。
【错因】对几何体的形状认识模糊不清。
【正解】B。A不能折叠成棱柱,缺少一个侧面;B能折叠成四棱柱;C不能折叠成四棱柱,有两个面重叠;D不能折叠成六棱柱,图中底面是五边形。
【点评】本题要注意几何体的上底面与下底面是相对的。
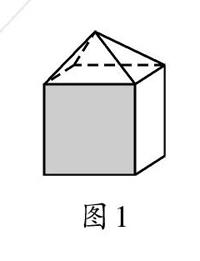
例2 如图1,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是()。
图1
A B C D
【错解】D。
【错因】没有抓住四棱柱的特征。
【正解】B。由平面图形的折叠及几何体的展开图解题,注意带图案的一个面不是底面。
【点评】同学们解题时切勿忘记正四棱柱的特征及正方体展开图的各种情形,做题时可亲自动手操作,增强空间想象能力。
例3 如图2,若添上一个正方形,使下图能折叠成一个正方体,且使相对面上的数字之和相等,则共有()种不同的添法。
图2
A.5B.4C.3D.6
【错解】C。
【错因】不会找相对面。
【正解】B。正方体的表面展开图中,相对的面之间一定相隔一个正方形。“1”与“5”是相对面,“2”与“4”是相对面,所以,要添加的是“3”的相对面。要满足题目要求,共有4种不同的添法。
【点评】正方体的表面展开图中,相对的面之间一定相隔一个正方形。确定出相对面,再根据相对面上的数字之和相等解答。
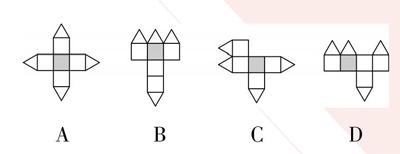
例4 下面四個图形中,经过折叠能围成图3所示的几何图形的是()。
图3
A B C D
【错解】C。
【错因】对图中三角形、圆、正方形所处的位置关系不清楚。
【正解】B。根据立体图形可得,展开图中三角形图案的顶点应与圆形的图案相对,而选项A、D与此不符;三角形图案所在的面应与圆形的图案所在的面相邻,选项C不符。故选B。
【点评】此题主要考查了展开图折叠成几何体的问题。同学们可以动手折叠一下,有助于空间想象力的培养。
例5 图4是一个正方体的表面展开图,则这个正方体是()。
图4
A B C D
【错解】D。
【错因】没有抓住展开图的特征。
【正解】C。通过具体折叠,结合图形的特征,判断图中小正方形内部的线段折叠后只能互相垂直,且无公共点。所以选C。
【点评】本题考查了展开图折叠成几何体的问题。从实物出发,结合具体的问题,辨析几何体的展开图,通过立体图形与平面图形的转化,建立空间观念是解决此类问题的关键。
例6 下列图形通过折叠能围成一个三棱柱的是()。
A B C D
【错解】A。
【错因分析】对三棱柱及其表面展开图的特点不清楚。
【正解】C。A折叠后得到三棱锥;B折叠后两侧面重叠,不能围成三棱柱;C折叠后能围成三棱柱,故本选项正确;D折叠后两侧面重叠,不能围成三棱柱。
【点评】本题考查了三棱柱表面展开图的问题。解题时注意:上、下两底面应在侧面展开图长方形的两侧,且是全等的三角形,不能有两个侧面在两个三角形的同一侧。
(作者单位:江苏省扬州市田家炳实验中学)

