横看成岭侧成峰 远近高低各不同

胡永强

一、画三视图——从空间到平面

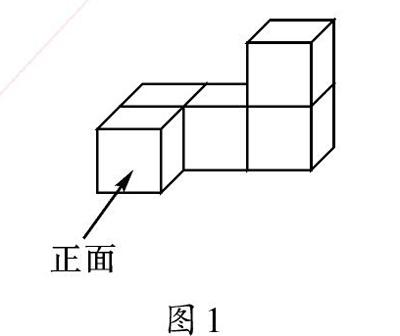
例1 图1是由5个棱长为1的正方体组成的几何体，请画出它的三视图。

图1

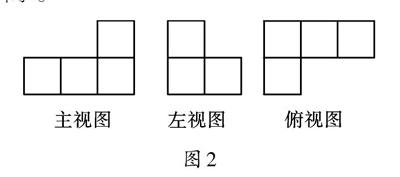
【分析】分别从正面、左面和上面看这个物体，想象出形状再画出来，如图2所示。

图2

二、还原几何体——从平面到空间

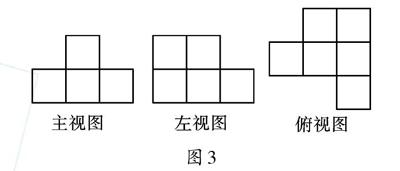
例2 如图3，在一个仓库里堆积着若干个正方体货箱，管理员要核实一下箱子的数量，于是就想出一个办法：将这堆货物的三视图画出来。你能根据所给的三视图，帮他算出箱子的数量吗？

图3

【分析】借助三视图还原几何体，通常先把俯视图作为地基，再结合主视图和左视图确定层数，并将层数写在俯视图的相应位置上，最后再统计总个数即可。如图4，共有8个箱子。

图4图5

三、综合问题

例3 如图5，在平整的地面上，放置着一个由若干个完全相同的小正方形堆成的几何体。如果现在还有一些相同的小正方体，要保持俯视图和左视图不变，最多可再添加几个小正方体？

【分析】此类问题要综合考虑。俯视图不变，说明地基不可变;左视图不变，说明每一行最高的不能变。基于这两条，可在第二列面朝我们的几何体上放1个小正方体，在这列后面的几何体上放2个小正方体;还可以在第三列面朝我们的几何体上放1个小正方体。最多可放4个。

（作者单位：江蘇省苏州市阳山实验初级中学校）