地层地质体模型与基坑拓扑无缝集成研究
何群,郭甲腾,王江梅,李鹏宇,杨传江
(东北大学资源与土木工程学院,辽宁 沈阳 110819)
1 引 言
随着三维地质建模和计算机技术的快速发展,城市地下空间开发的深度和广度逐步加大,传统二维地质图件(平面地质图、剖面地质图、钻孔柱状图等)在描述和表达地下地质构造的空间发育特征方面愈显不足。因此,二维图件逐渐被三维地质模型所代替,三维可视化技术也在地质领域中得到广泛应用,例如地质[1~4]、成矿预测[5]、地形地貌[6]等。地质模型可视化成为工程技术的一个重要研究内容,可以帮助地质工作者在动态场景中进行思考和推理。本文基于地质体的基坑开挖应用开展研究,通过对基坑开挖体和开挖后的地质体进行三维建模和可视化分析,可为建筑施工提供理论方法和技术支撑。因此,实现基坑开挖体与开挖后地质体的拓扑无缝集成,对于实现工程的科学管理、提高工程的信息化、智能化决策水平,具有重要的现实意义和应用价值。
三维地质建模的数据模型是三维地质模型可视化的基础与核心[7]。近年来,众多学者已经在数据模型方面进行了大量研究,部分学者也对现有三维地质建模数据模型进行了总结。概括来说,主要有矢量边界表达方法、体元法和混合方法三种类型。由于三维数据模型理论与技术仍未成熟,已有的矢量模型、表面模型、体元模型等数据模型都有一定的局限性,不同类型模型的混合模型构模流程又过于复杂且空间分析效率低,往往只注重刻画模型外表,而忽略了开挖体内部结构的空间分析和属性表达。在基坑开挖体建模方面,现有的开挖算法,大都是首先建立一个开挖实体(比如基坑实体),然后用基坑侧面所在的几个平面与地层体做布尔减运算,通过减去位于基坑平面内的实体来实现基坑的开挖建模。这种开挖算法,没有建立起独立的分层基坑体模型,且割裂了基坑开挖体与开挖后地质体的相互联系,缺乏地质工程的集成与联动机制。现有的算法大部分只实现基坑工程的可视化,但忽略了开挖体与地质体的无缝集成,且不便于基坑开挖体的单独显示及进一步可视分析,难以为现有的工程地质工作者提供分析和指导。因此,本文将广义三棱柱和平面拉伸建模方法相结合,建立了地质体和基坑开挖体的集成模型,使两模型间进行拓扑无缝重构,从而解决了基坑与地质体的几何无缝开挖问题。
2 地质体和基坑开挖体三维模型的建立
2.1 地质体模型建立与剖分的原理和方法
本文建立地质体模型采用的是基于Delaunay三角剖分的TIN表面模型与体元模型相结合的广义三棱柱模型(GTP)[7~9]。其中,建立TIN的离散点是由工程中的钻孔数据生成,钻孔是工程地质勘查中经常使用的方法,是获取三维建模所需信息的主要途径。通过钻孔资料,可以直接获得地层信息和结构面信息,包括地质勘探孔的位置、孔深、层位、结构面的位置和性质[10]。考虑到Delaunay三角形的良好特性,本文使用Delaunay三角网,对离散的钻孔数据构建连续覆盖整个区域的三角网。其关键问题是确定哪三个离散数据点构成一个最佳三角形,并使得每个离散采样点均成为三角形的顶点[11]。
广义三棱柱(Generalized Tri-Prism,GTP)是用上、下两个不平行的三角形集合和三个侧面的四边形所组成的。其基本思想是通过上、下不平行的TIN面来表达不同的地层面,通过侧面的空间四边形面来描述同一层面间相邻三棱柱的空间邻接关系,用GTP柱体来表达层与层之间的内部实体[3]。为了实现模型的无缝集合,便于地质体与基坑体之间的求交运算,需要转化剖分GTP,即提取出GTP体元的三角形面[12,13],并标记处上、下底面三角形;对于GTP体元的非三角形面,通过最小顶点法[9]剖分成两个三角形,从而将GTP地质模型转化为由三角形组成的边界表示模型。
2.2 基坑开挖体模型建立与剖分的原理和方法
本文中基坑工程研究的是垂直深基坑,开挖边界线大部分是不规则的多边形,对于开挖体建模借鉴的是基于平剖面拉伸的方法实现的。其方法如图1所示:
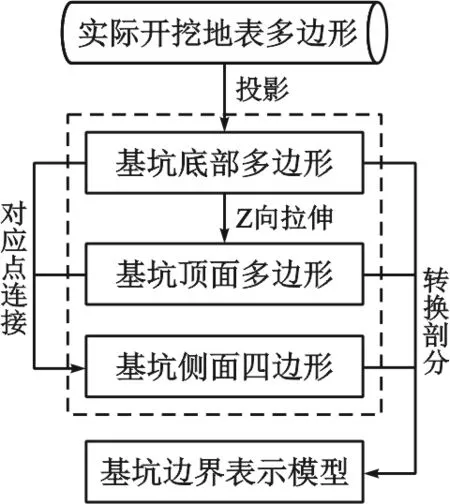
图1 基坑模型建立流程
Step1:获取基坑底部多边形。通过实际开挖地表多边形顶点A′B′C′D′E′投影点的依次连接,获得基坑底部多边形。
Step2:构建高出地表的基坑顶面多边形。把底部多边形ABCDE沿法向平移至高出地表位置,获得基坑顶面多边形,如图2所示。

图2 沿法向平移建立基坑模型
Step3:构建基坑侧面多边形。依次相连上下两个面的顶点,获得多个侧面多边形。
Step4:构建基坑边界表示模型。通过把上述步骤构建的基坑底部多边形、基坑顶面多边形、基坑侧面多边形分别转化剖分,获得三角形组成的边界表示模型,如图3所示。
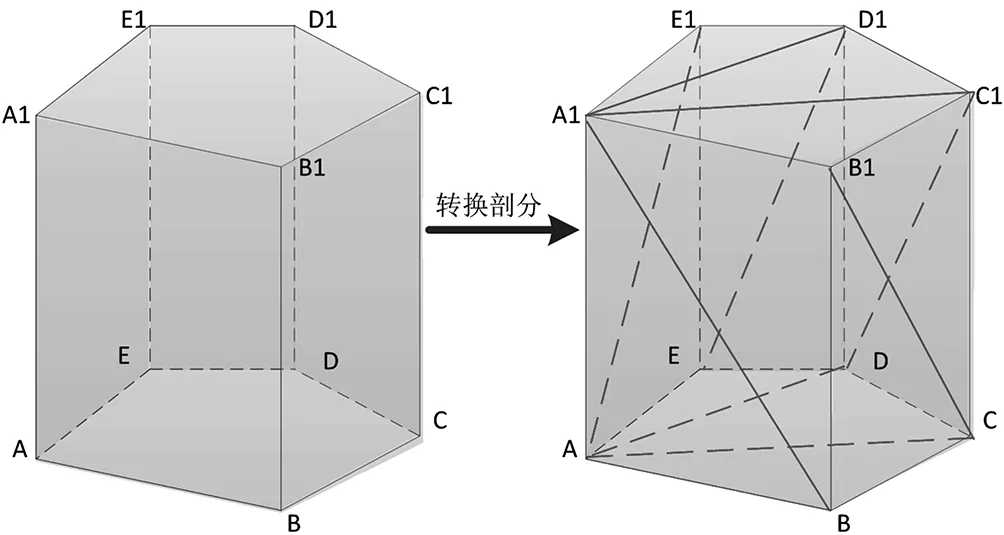
图3 基坑转化剖分
3 基于地质体模型和基坑的拓扑无缝集成原理
3.1 拓扑无缝集成原理
实现拓扑无缝集成的实质就是在基坑开挖体和地质体之间的布尔运算[14~17]。本文实现基坑工程的拓扑无缝集成开挖,就是运用布尔运算对三角形集合表示的封闭基坑模型和地层模型进行布尔交、布尔减运算,如图4所示。如此一来,就可以获得基坑开挖体模型(地层边界表示模型与基坑边界表示模型的交集)和开挖后地质体模型(地层边界表示模型与基坑边界表示模型的差集)。布尔运算的运用也保证了其交界面处拥有相同的三角形集合,从而实现基坑工程的拓扑无缝集成开挖。
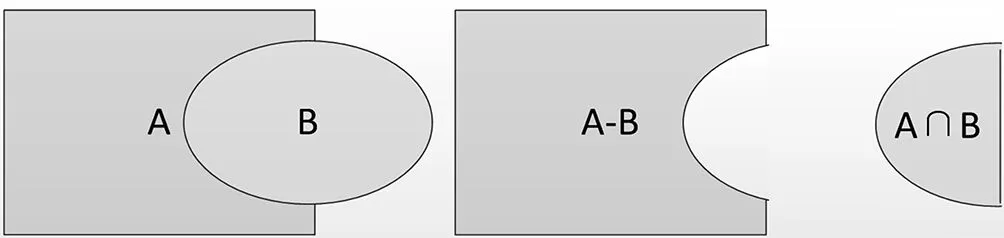
图4 实体布尔运算说明
3.2 三角形自分解算法与结果优化
在三维地质建模中,不规则三角网在表示复杂表面方面有诸多优越性,如结构固定、处理简单、保持测量数据的原始性。因此,本文利用不规则三角网的优良特性,借鉴文献[1,2]的Delaunay三角剖分算法,提出了三角形自分解算法。通过将一个三角形分解为多个三角形的方法,使地质体和基坑开挖体在拓扑重构后产生的不规则多边形仍可分解成多个三角形,来保证模型体边界始终由三角形包围。具体流程如下:
(1)三角形自分解:
当某一个三角形与其他多个三角形组成的几何体进行布尔运算时,会有交点和交线,如图5(a)所示。计算完交点坐标后,通过以下两步即可完成三角形自分解:
首先,处理位于三角形内部的交点。当交点位于三角形内部时,如图5(b)所示,通过连接交点与三个顶点进行三角形自分解,即将一个三角形分解为三个三角形。
其次,处理位于三角形一边上的交点。当交点位于三角形一条边时,如图5(c)所示,通过连接交点与此边相对应的顶点完成三角形的自分解,即将一个三角形分解为两个三角形。
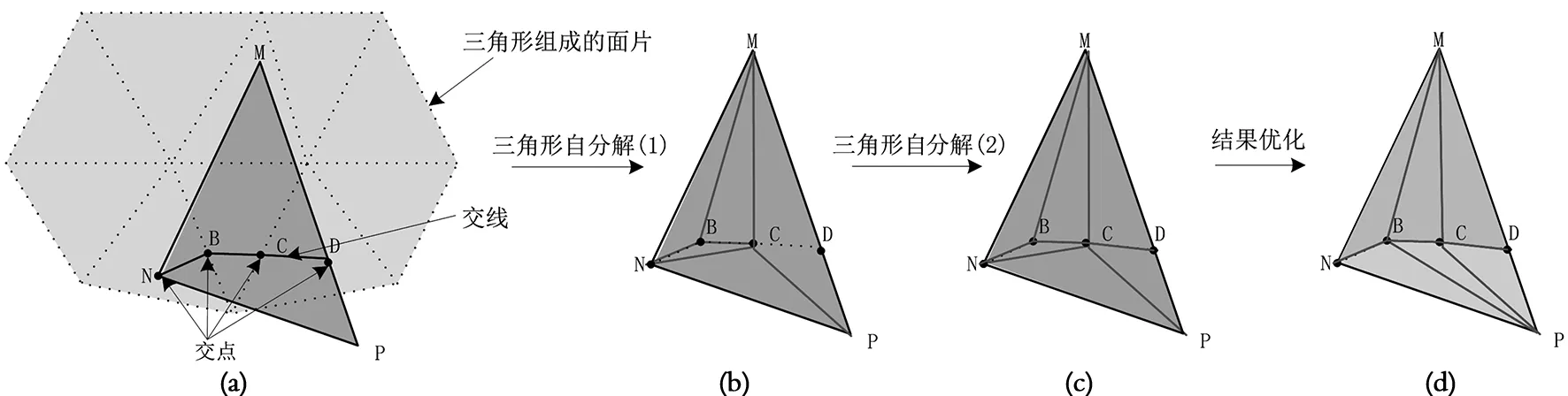
图5三角形与三角形面片相交
(2)结果优化:
三角形自分解完成后,可以获得三角形组成的初始不规则三角网,同时获得了三角形的拓扑关系,如图5(d)所示。但是,这样构成的三角网并不能满足Delaunay三角网准则,所以,有必要在所有三角形自分解完成进行结果优化。可以看到,交线已经将原来的三角形分为属性不同的两部分。本文在三角形自分解的基础上,通过搜索交线的影响域,对属性不同的三角形集合进行重新三角剖分完成结果优化,让交线对三角形自分解结果进行修订,以构成既满足Delaunay三角网准则、又能实现布尔运算的不规则三角网。
4 基坑与底层地质模型无缝集成方法
通过广义三棱柱模型(GTP),可以构建基坑和地质体的三角形组成的边界表示模型,进而实现基坑模型与地质体模型的多层剖分与集成。本文就多层基坑的无缝开挖建模流程说明如图6所示:

图6 基坑无缝多层开挖流程
Step1:构建基坑和地层的边界表示模型。通过将广义三棱柱方法应用于钻孔数据,构建地层的边界表示模型;通过2.2节介绍的方法构建基坑的边界表示模型。
Step2:三角形自分解与属性判别。通过3.2节介绍的三角形自分解算法,对步骤1中获得的基坑体和抽取的地层体边界表示模型的某一地层进行布尔运算,并通过交线进行三角形属于基坑体或开挖后地质体的属性判别。
Step3:提取边界表示模型。步骤2中,基坑边界表示模型与地层边界表示模型的交集就是含地层的基坑体模型,二者的差集就是开挖后地质体模型。通过提取边界,即可分别获得含地层的基坑体和开挖后地质体边界表示模型。
Step4:上述三个步骤完成了某一地层与基坑模型的布尔运算、三角形自分解以及属性判别。在此基础上,依次对每一个地层进行上述操作,即可获得开挖后的多层地质体模型和开挖出的多层地质体模型。
5 实验案例
辽宁体育训练中心位于辽宁省沈阳市于洪区黄河北大街,地形平坦,地面高程介于 49.23 m~57.71 m。共布设127个钻孔,勘探深度为 7.0 m~30.0 m。本次研究使用实际工程资料,建立了开挖后地质体模型(如图7所示)和基坑开挖体模型(如图8(a)所示)。本次实验,在建立的基坑开挖体模型的基础上,将基坑体进行有限元剖分,如图8(b)所示。

图7 挖后地质体

图8 基坑体的有限元剖分
6 结 论
本文基于广义三棱柱模型和平面拉伸法相结合的方式建立了三维地质体模型,依据模型外围的界面三角形剖分原理,提出了三角形求交以及三角形自分解的算法,通过布尔运算建立了施工后基坑开挖体和地层体的多层模型,实现了基于地质体模型的多层基坑开挖与几何无缝集成,结合真实应用案例进行了方法验证,为岩土工程基坑体与地质体的空间集成建模与分析提供了一条可行的解决途径。同时,基坑体的有限元剖分结果可以协助工程设计人员在基坑设计过程中充分考虑土层的力学性质以及对周边地层结构的稳定性影响,对于岩土工程设计分析和指导实际工程具有重要意义。

