基于改进随机蛙跳算法的主梁轻量化研究
靳通通,吴淑芳,李 松,王腾飞
(1.中北大学机械工程学院,山西 太原 030051)(2.山西省起重机数字化设计工程技术研究中心,山西 太原 030051)
主梁是桥式起重机的主要承重部件,其结构轻量化及拓扑优化是比较热门的研究方向。李志雄等[1]采用改进的人工蜂群算法对主梁进行轻量化设计,朱学敏[2]使用免疫蚁群算法进行了主梁的拓扑优化研究。目前起重机主梁轻量化问题还没有公认的解决方案,因此需要进一步对主梁的轻量化问题进行探讨。
随机蛙跳算法(shuffled frog leaping algorithm , SFLA)是一种综合了多种其他智能算法思想的新型亚启发式算法。2003年,Eusuff等[3]在解决资源网络优化问题时首次应用了随机蛙跳算法。由于SFLA具有容易理解、易于实现、寻优能力均衡等特点,因此对其进行改进研究和应用已成为学术界的热点问题。孙冲[4]把量子算法的思想引入到SFLA中,发展出了一种全新的量子蛙跳算法。姚应龙[5]使用加速和老化机制改善SFLA,得到了较好的优化效果。目前对于SFLA的研究与应用主要集中在控制器参数调节问题、聚类问题及离散优化问题等,较少涉及到结合工程实际的函数寻优问题。在理论上,SFLA同样适用于工程实际中的函数寻优,值得进一步讨论。
主梁轻量化问题实际上就是带约束的函数寻优问题。本文针对SFLA解决带约束的函数寻优问题时,局部探索能力变差、优化结果不理想、收敛慢等缺点进行了两方面的改进,并把改进后的SFLA引入到桥式起重机主梁轻量化问题中,验证算法改进后的实际性能。
1 随机蛙跳算法的简介与改进
1.1 随机蛙跳算法简介
随机蛙跳算法模拟了青蛙在湿地中跳动觅食的行为,每个青蛙可以看作一个解,而湿地看作是给定的解搜索空间。
一群青蛙被分成多个族群,在每个族群中进行局部搜索:族群中的青蛙依照制定的进化搜索策略,找到组内最好与最差的青蛙个体,对最差的青蛙用类似粒子群算法的进化方法进行位置调整,将位置调整视为一次跳跃[6]。
局部搜索达到一定的次数后,采用联合体进化算法进行族群混合(即族群间的思想交流),局部搜索和族群混合的过程循环进行,直到满足结束条件[6]。全局性的思想交流与局部的进化搜索相结合,使得SFLA具有较强的调节性和扩展性。
1.2 随机蛙跳算法的改进
设共有F个青蛙,表示为X(1),X(2),…,X(F)。第i只青蛙用向量X(i)=(X1,X2, …,XL)表示,L代表每只青蛙的信息元素个数。在寻优问题中,寻找使得目标函数值最小的解。
1.2.1评价值函数的改进
采取一种新的方法来计算每只蛙的评价值,X(i)的评价值evali为
(1)
式中:f[X(i)]为X(i)对应的函数值;T为一个可调的系数,T>0。
式(1)建立了每只蛙的评价值与其目标函数值的一一对应关系,而且函数值越小对应的评价值就越大。算法运行过程中,由于函数值变化可能较大,既有可能出现过早收敛,也有可能后期收敛速度太慢。式(1)中通过调节T的大小,可以合理控制评价值的相对大小,避免上述不利情况发生。
1.2.2蛙跳方式的改进
设Xb和Xw为族群中的最优蛙和最差蛙,接下来进行局部进化以更新最差蛙Xw的位置。在标准的SFLA中蛙跳方式[6](即最差蛙更新方式)如式(2)和式(3)所示:
S=rand·(Xb-Xw)
(2)
(3)
上述的蛙跳方式会使得最差蛙更新后的位置处于原来的最差位置与和最优位置之间,这样就限制了蛙跳的范围,容易导致收敛变慢或者早熟,因此将式(2)做如下改进:
S=C·rand·(Xb-Xw)
(4)
式中:C为大于1的常数,但是C不能设置得过大。
考虑到每一只青蛙在觅食过程中都有停留在当前位置的可能,因此通过运动惯性来描述这种现象,将式(4)中的蛙跳步长做进一步改进:
S(k)=w·S(k-1)+C·rand·(Xb-Xw)
(5)
式中:S(k)为以k为变量的跳跃步长;k为迭代次数;w为运动惯性的权重系数,w越大全局搜索能力越强,w越小局部搜索能力越强。在局部搜索开始时将w设置成较大值,然后逐渐减小它,进而找到最佳值。加入运动惯性虽然会使收敛速度略微降低,但是会使得搜索过程更加平稳,可以提高全局搜索能力。
1.3 改进SFLA算法流程
1)初始化各个参数。
2)在给定的约束条件下,随机生成F个青蛙作为初始蛙群, 表示为X(1),X(2),…,X(F)。按照式(1)计算各个青蛙的评价值evali。
3)将F个青蛙按评价值大小降序排列,记录最优蛙位置Px=X(1)。将蛙群数组X分成m个族群,记为Y1,Y2,…,Ym。每个族群包含n只蛙,第1个蛙进入Y1族群,第2个蛙进入Y2族群,…,第m个蛙进入Ym,第(m+1)个蛙进入Y1族群,…直至所有蛙进入指定族群[7]。
4)在每个族群进行局部搜索。
①设im=0,im为族群计数器,上限为m;设iN=0,iN是局部进化的计数器,上限设为LS。
②记录当前族群的最优蛙Xb和最差蛙为Xw,im=im+1。

④如果步骤③没有改进最差蛙的位置,则在湿地中随机产生任意位置的蛙,取代最差蛙,并验证更新后的位置是否满足约束条件,如不满足转到步骤③。
⑤若iN ⑥若im 5)每个族群进行过一轮局部搜索后,将各个族群中的蛙重新混合并排序,再生成新的族群,记录此时最优蛙位置Px。 6)如果满足算法终止条件,即停止算法,否则转到步骤4)。 寻优问题中的主梁属于箱型梁,主要由盖板、腹板以及若干筋板组合而成。主梁的质量为这些结构的质量之和,本文将主梁简化为等截面梁,且忽略筋板,那么主梁截面面积与主梁的质量成正比。主梁截面形状如图1所示。 x1—腹板高度;x2—副腹板厚度;x3—上下盖板厚度;x4—上下盖板的宽度;x5—主腹板厚度 本文以某公司使用的32t-25.5m-10m的双梁小车式桥式起重机的半偏轨式箱型主梁结构为研究对象,工作级别为A6。设定变量参数选取范围见表1。 表1 变量参数选取范围 mm 1)主梁优化目标函数。 设定截面面积为优化目标,其数学表达式为: minf(x)=x1(x2+x5)+2x3x4 (6) 2)约束条件的确定。 以国标GB/T 3811—2008[8]与《起重机设计手册》[9]的相关要求为依据,确定箱梁结构轻量化设计中的约束条件包括强度约束、刚度约束、疲劳约束和稳定性校核等。 选取遗传算法(GA)、SFLA算法与改进后的SFLA算法进行寻优问题的对比分析。设定迭代次数最大为300。对于遗传算法把种群规模设为300;SFLA算法和改进后的SFLA算法中,令m=20,n=15,故初始蛙群个数F=300。根据这3种算法编制MATLAB程序,运行MATLAB程序40次,随机选取其中一次运行结果,得到寻优曲线如图2所示。 图2 不同算法寻优曲线 由图可知,SFLA算法和改进SFLA算法明显比GA算法优化结果好。SFLA算法在260代左右才收敛,收敛速度慢,运算过程中容易出现停滞现象。改进后的SFLA算法在140代实现了收敛,且最终优化结果好于未改进的SFLA算法,优化过程是三者中最为平稳的,另外两者都容易出现不同程度的停滞现象。在40次测试中,改进后的SFLA算法优化结果稳定,而SFLA算法与GA算法的优化结果经常出现波动。 保留优化程序运行40次后的最佳优化数据,得到GA算法、SFLA算法和改进后的SFLA算法的最优解见表2,其中f(x)为目标函数。 表2 3种算法最优解对比 为了便于制造,腹板厚度和盖板厚度一般要取整数,腹板高度和盖板宽度一般取10mm的整数倍。主梁的初始数据和经过圆整处理后的最佳优化数据见表3。 表3 不同优化方案的数据对比表 由表可知,箱型梁截面积最小化的寻优过程中,使用改进SFLA算法得到了最好的优化结果,截面面积比初始值减少了17.30%,进一步计算可知,比GA算法减少了4.91%,比SFLA算法减少了1.03%。 依据改进SFLA算法的优化结果设计出主梁的三维模型,并将建好的模型导入ANSYS Workbench中进行处理。主梁材料设置为Q235,选取100mm大小的六面体网格单元对主梁进行网格划分,划分得到61 340个节点,36 870个单元。 使用ANSYS Workbench分析当小车处于主梁跨中位置且起重机满载时的工况,主梁一端固定,一端简支。经过软件求解得到主梁的应力云图和变形云图如图3,4所示。 由图3可知,由起重机满载载荷引起的主梁最大应力为116.26MPa。已知材料为Q235,起重机的工作级别为A6,其许用应力为[σ]=135.66MPa。由此可知,主梁最大应力小于许用应力,满足应力要求。由图4可知,主梁的跨中位置变形最大,最大的变形量为13.837mm,而许用垂直静刚度为[f]=31.875mm,由此可知,最大变形量小于许用垂直静刚度,符合静刚度要求。 图3 主梁应力云图 图4 主梁变形云图 本文对SFLA算法进行了两点针对性改进,将GA算法、SFLA算法与改进后的SFLA算法都引入到主梁轻量化问题中,通过起重机主梁的具体优化实例证明了改进后的SFLA算法在收敛速度和优化结果两方面都优于其他两种算法。通过静力学分析可知,采用改进SFLA算法优化后的主梁结构符合刚度和应力约束条件,验证了用改进SFLA算法解决箱型梁轻量化问题的可行性。2 桥式起重机主梁轻量化的数学模型


3 实例验证
3.1 实例分析
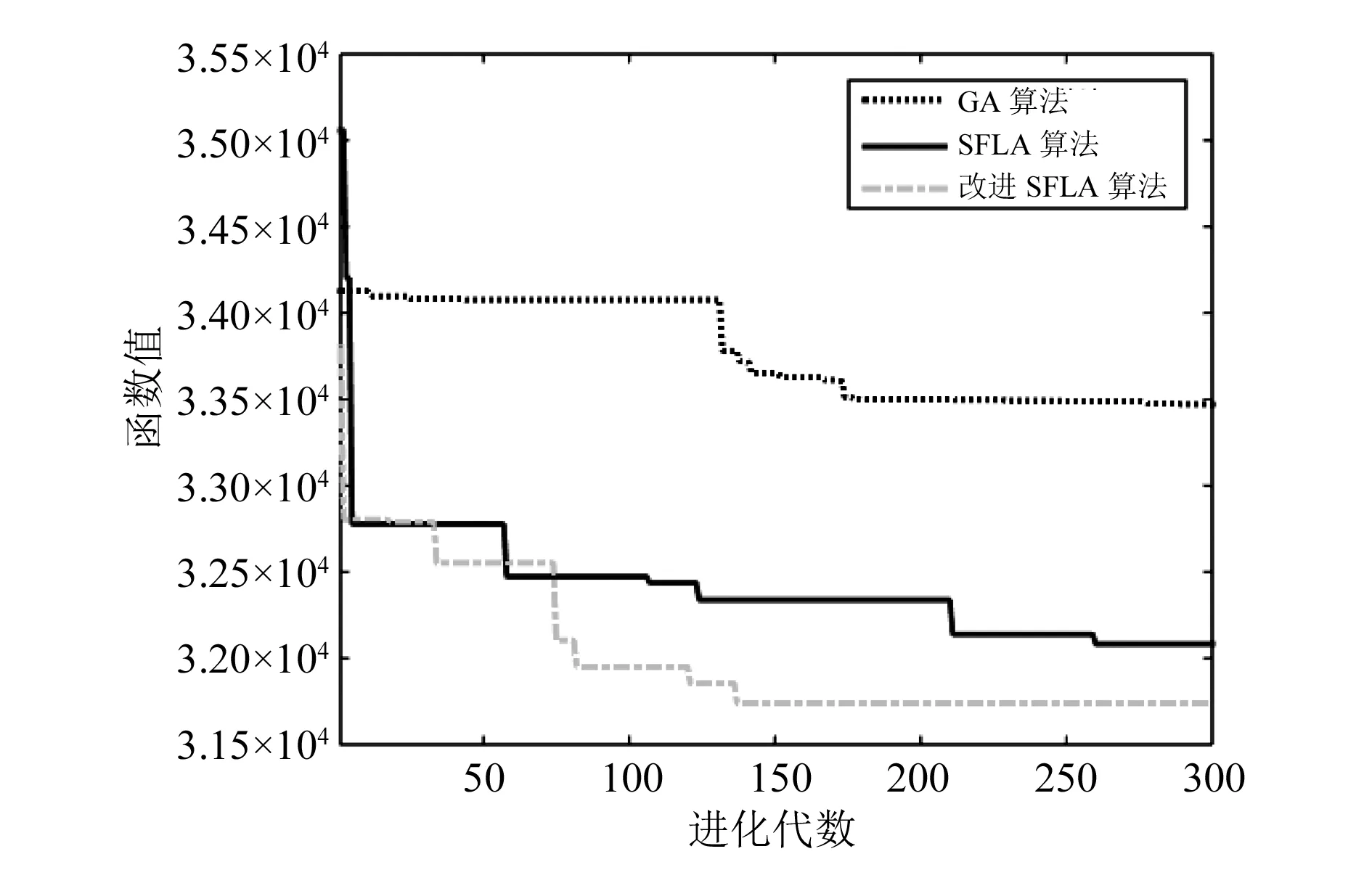
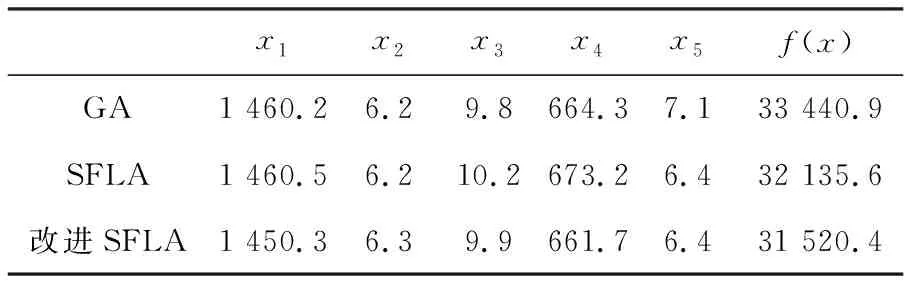

3.2 优化结构静力学验证

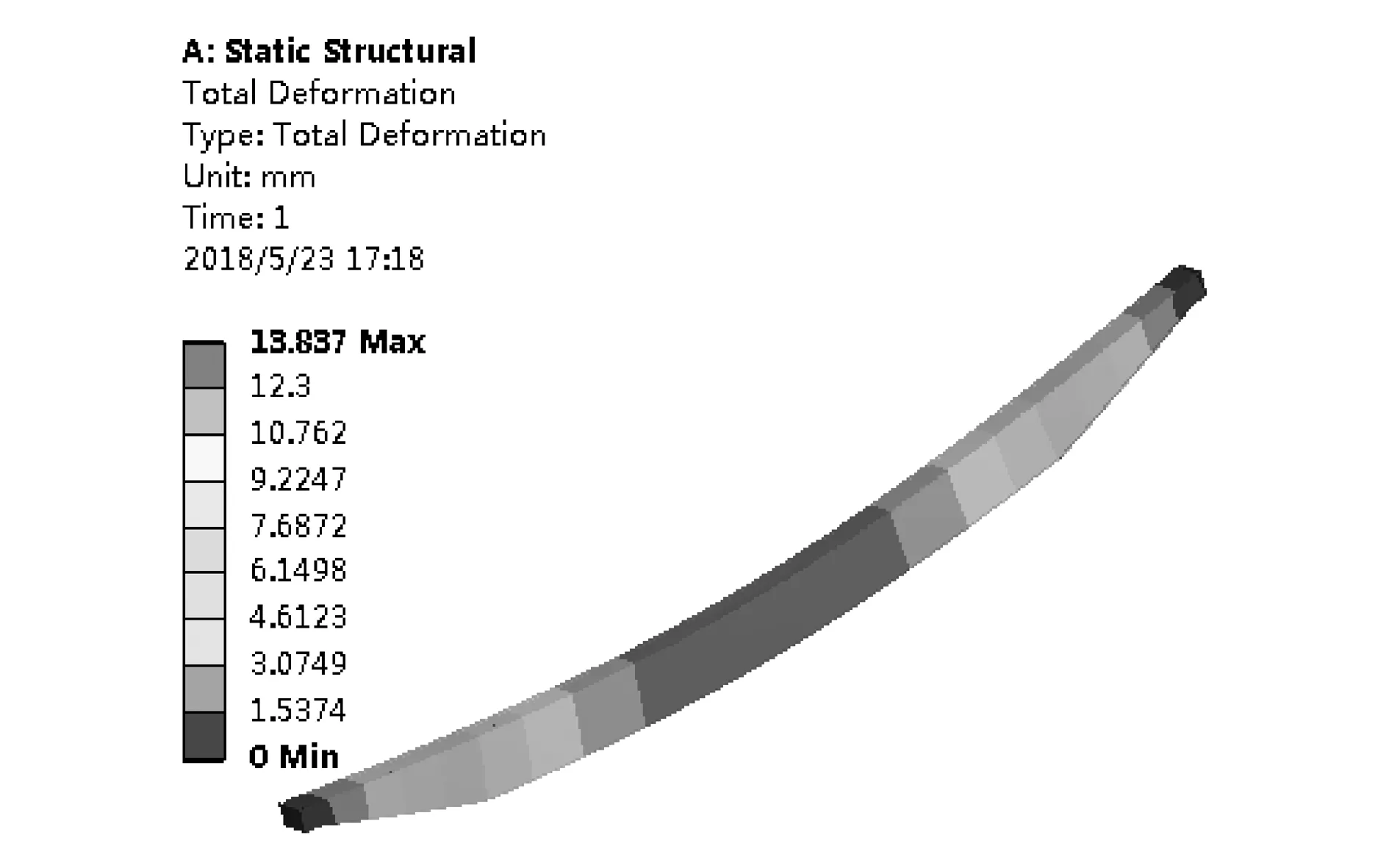
4 结束语

