单服务器队列的仿真分析

李龙镇

（延边大学工学院，吉林延吉，133002）

0 引言

单服务器队列(M/M/1)存在于社会生活中的方方面面，比如电话交换机系统、路由器缓冲区、铁路购票系统、商场付款队列、理发店排队理发队列等，因此出现了很多对单服务器队列的研究文章，并取得了一定的成果[1～4]。

本文利用概率与数理统计学上的概率分析工具，通过分析和导出单服务器队列的概率统计模型，导出了泊松分布模型，并以泊松分布模型为基础导出了指数分布模型，并以此为基础导出了单服务器队列的仿真模型，最后利用计算机网络仿真软件OPNET对单服务器队列进行了详细的仿真分析，确定出服务器的数据处理速度与队列中的数据等待时间的相互关系，并以图形方式直观地加以表示。

1 单服务器队列的概率统计模型分析

1.1 泊松分布

为了导出泊松分布统计模型，我们以传统的电话交换机为例，假设在时间段[0,t]内在随机时间X1,X2,…有电话呼叫到达电话交换机。在这里我们做了两个假定：

①同质性：电话呼叫到达的速率λ对时间来说是个常数；

②独立性：在不同的时段内到达的电话呼叫数是独立的随机变量。

设定在区间[0,t]内到达的电话呼叫个数为Nt，则根据同质性可以得出Nt的期望值E[Nt]=λt。把区间[0,t]划分为n个相同小段，则每个小段区间为t/n。当n足够大时，每个小段内呼叫数只能是0或者1。设定Rj为第j个小段内的呼叫数，则Rj只能是0或者1，Rj满足概率值为pj的伯努利分布，即pj=λt/n。在区间[0,t]内的所有呼叫总数可以表示为：

因为每个Rj是具备独立性的随机变量，所以Nt满足二项式分布。由此我们得到：

因为：

组合以上公式，我们得到：

设定µ等于λt，则得到标准的泊松分布：

1.2 指数分布

我们定义 Ti=Xi-Xi-1为相互时间间隔，定义T1=X1为呼叫第一次到来的时间。为了观察T1的概率分布，我们关心在t时间之后第一次呼叫到来的情况，即在[0，t]时间段没有呼叫到来，可以用下面的公式表示：

即：T1满足参数为λ的指数分布，对于T2我们假定T1=s，然后计算它们的条件概率：

由于公式结果与s无关，所以我们得出T2满足指数分布，即：

同理对任何Ti都能导出其满足指数分布，所以我们得出结论：对具有参数λ的泊松分布X1，X2，X3，…来说，其X1，X2-X1，X3-X2，…是独立的随机变量，都满足具有参数λ的指数分布。

2 单服务器队列的仿真模型分析

为了能用计算机程序设计仿真单服务器队列，需要求出泊松分布或者指数函数的反函数。但由于无法求出泊松分布的反函数，所以重点就是求出指数函数的反函数。设定指数函数的分布函数为F(x),其反函数为Y,均匀分布函数为U，则可以实现下面的公式：

设定F(x)=u,则：

由于1-u和u都是分布在(0，1)之间的均匀分布函数，为了方便计算，可用u代替1-u，所以最终反函数可用下式表示：

由于任何计算机程序设计语言都具备产生(0,1)之间随机数的随机函数，所以可利用该公式对指数函数进行模拟，即对单服务器队列进行仿真分析。为了简化解决问题的复杂度，可以采用现有的仿真软件，而不是利用某个计算机语言编程对其求解，所以本文采用已有仿真功能的OPNET[5～6]计算机仿真软件对单服务器队列进行仿真分析。

单服务器队列在OPNET的节点图如图1所示，数据源模块的设定如下：分组相互时间间隔为Exp(1)秒,分组大小为Exp(9000)位元，处理模型为acb_ fi fo，即先进先出队列。在OPNET中，队列本身包括缓冲区和处理器，队列的设置如下：队列处理器的处理速度为9600位元。由于处理完的分组继续占据内存，影响计算机系统的效率，所以再加上退出模块，负责销毁处理完毕的分组。仿真分析的重点在分组相互时间间隔、分组的大小以及队列处理器的处理速度对队列中的分组平均延迟时间的影响。为了简化问题分析方法，我们假设分组相互时间间隔以及分组的大小不变，只是通过调整队列处理器的处理速度来分析队列中的分组平均延迟时间，通过多次仿真分析，发现在现有的条件下，即队列处理器的处理速度为9600位元情况下，下调600个位元，即队列分组处理器的处理速度为9000位元时，队列的平均延迟时间开始增长，不趋向于稳定。即系统缓冲区里的分组越来越多，最终导致系统崩溃。而当对处理器的处理速度设为10200位元时，队列的平均延迟时间开始减少，大约一直减少到8秒左右。这对于实际情况也非常符合，即处理器的处理速度越快，队列里的待处理事项也会越来越少。

图1 OPNET仿真单服务器队列的模块图

图2为图1模块图的仿真结果，在这里分组相互时间间隔为Exp(1)秒,分组大小为Exp(9000)位元，处理模型为acb_ fi fo，队列处理器的处理速度为9600位元，从仿真结果可以看出平均延迟时间大约为15秒，系统随着仿真时间的延长趋于稳定。

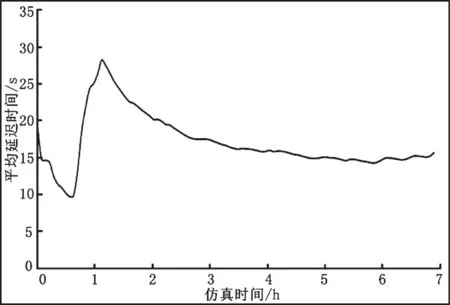
图2 队列处理器速度为9600时的分组平均延迟时间

图3为图1模块图的仿真结果，在这里分组相互时间间隔为Exp(1)秒,分组大小为Exp(9000)位元，处理模型为acb_ fi fo，队列处理器的处理速度为9000位元，可以看出队列中分组平均延迟时间随着仿真时间在同步增加，即队列中等待处理的分组数目不断增加，导致系统发生堵塞，最终会引起系统崩溃。

图3 队列处理器速度为9000时的分组平均延迟时间

图4 队列处理器速度为10200时的分组平均延迟时间

图4为图1模块图的仿真结果，在这里分组相互时间间隔为Exp(1)秒,分组大小为Exp(9000)位元，处理模型为acb_ fi fo，队列处理器的处理速度为10200位元，可以看出队列中分组平均延迟时间大约为8秒，系统随着仿真时间的延长趋于稳定。

3 结论

由于单服务器队列应用于现实社会中的各个角落，所以对其分析显得非常重要。本文以单服务器队列概率与数理统计模型入手，首先进行了详细的理论分析，用概率与数理统计方式导出泊松分布和指数分布，然后再导出指数分布的反函数，即单服务器队列的仿真函数，再用计算机网络仿真软件OPNET对其进行了仿真分析，主要以改变队列处理器的数据处理速度来分析队列中的分组平均延迟时间，通过仿真结果可以看出队列处理器的数据处理速度对于延迟时间起到非常重要的作用，队列处理器数据处理速度低，则延迟时间一直在上升，导致队列内等待处理的分组数目不断上升，最终导致系统堵塞以至崩溃。至于分组相互时间间隔和分组大小对单服务器队列的影响有待于以后进一步的研究。