沿临近空间机动弹道的扰动引力重构模型优化
周欢, 丁智坚, 郑伟
(1.中国工程物理研究院 总体工程研究所, 四川 绵阳 621999; 2.中国空气动力研究与发展中心, 四川 绵阳 621000;3.国防科技大学 航天科学与工程学院, 湖南 长沙 410073)
0 引言
滑翔弹道是高超声速滑翔飞行器全程弹道的主要组成部分,受地球扰动引力场影响显著[1]。有关计算结果表明,由扰动引力引起的滑翔弹道终端位置偏差可达几十千米[2],因此有必要在弹道计算和制导解算中考虑扰动引力的影响。实际上,地球外部空间扰动引力的求解问题属于地球物理和大地测量领域的传统问题,相关学者已经提出了若干高精度计算方法[3-4]。但是,这些方法通常具有计算规模大、数据存储量大、计算时间长的特点,无法满足弹上实时计算对轻量化和计算效率的要求。目前,有资料表明,唯一用于弹道导弹扰动引力模型射前构建的是点质量法[5-6],然而该方法欲求解空间任意一点的扰动引力需基于多层点质量数据对大量扰动质量的引力进行求和,不能适应发射快速性的要求。为提高解算速度,一些学者探讨了谱方法、数值逼近方法和有限元方法在扰动引力快速计算中的应用[7-11],但均未见其在飞行器应用中的相关报道。Zhou等[10]针对弹道导弹扰动引力实时补偿问题,提出了一种基于标准弹道构建飞行管道的局域表征理论,该方法能够有效地解决沿惯性弹道的扰动引力实时计算问题,但并不适用于本文探讨的临近空间侧向大范围机动弹道。
针对上述问题,本文提出了一种沿滑翔弹道的扰动引力快速重构方法,并分别以重构精度和数据存储量为优化目标,基于多岛遗传算法[12]获得了给定精度要求下的存储量最小模型和给定存储量要求下的精度最高模型。在求解优化问题时,为避免针对原始模型进行优化时引入难以容忍的计算量,基于最优拉丁超立方试验设计方法[13]和径向基函数(RBF)神经网络[14]构建了原始模型的代理模型。最后,通过仿真算例分别对快速重构模型、代理模型以及优化模型进行了校验。仿真结果表明,重构方法可有效地适应机动飞行下的复杂环境,在满足弹载计算机存储量要求的前提下大幅度提高了弹道终端精度。
1 扰动引力重构模型的建立
基于有限元思想建立沿滑翔弹道的扰动引力重构模型。由于有限元方法的求解精度取决于网格划分和逼近函数,当计算点超出逼近区间时精度将急剧下降,因此重构模型需确保计算点严格位于逼近区间内部。基于这一原则,确定如下重构流程:
1)根据滑翔弹道起点和终点,建立覆盖所有可行弹道的Field重构模型,模型参数存储在地面设备中;
2)根据飞行任务快速规划一条参考弹道,基于Field模型数据库和参考弹道构建Channel重构模型,模型参数存储在弹上;
3)基于延拓逼近理论完成飞行过程中的扰动引力实时解算。
1.1 沿滑翔弹道的空域剖分建模
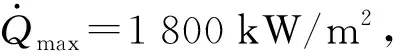

表1 不同射向滑翔弹道包络侧向最大宽度
注:左边界、右边界为沿射线方向的左边界和右边界。
由表1可以看出,在射程相同情况下,东向发射的滑翔弹道具有最大侧向机动范围。因此,计算射向为正东、射程不同的滑翔弹道侧向包络,并据此建立弹道包络宽度和射程的对应关系。除滑翔结束点经度和纬度不同外,其余仿真条件不变。仿真得到不同射程东向发射滑翔弹道对应的包络侧向最大宽度(见表2)。
考虑初态误差和飞行过程中的偏差,取1.5倍侧向弹道包络宽度作为建立侧向包络数学模型的依据。令射程为L,1.5倍弹道包络侧向宽度为W,可获得弹道包络最大宽度关于射程的函数,考虑飞行器本体建模误差和地球物理环境因素建模误差,纵向包络按照沿参考轨迹上下浮动±10 km考虑,可建立滑翔弹道三维包络的数学模型,具体如图1所示。

表2 不同射程东向发射滑翔弹道包络侧向最大宽度
W=-1.064 813L+0.000 879L2-
1.225 047e-7L3+4.607 571e-12L4.
(1)
为简化Field空域剖分算法,引入一种基于极点变换思想的换极坐标系。换极坐标系以滑翔弹道起点和终点确定的大圆弧平面作为重新定义的赤道平面,称为换极赤道平面。Field空域在换极坐标系中沿换极赤道平面对称分布,因此可采取沿换极后经纬网正交的空域剖分策略,从而简化空域剖分算法。
记换极后的Field空域为Ω. 在换极地球固定球坐标系中,可将Ω描述为具有一定厚度的球壳。按照适当的网格大小将Ω均匀剖分为m个互不重叠的子域Ωe(e=1,2,…,m),获得换极节点坐标。经坐标变化[12],可由换极节点坐标获得一般坐标系中的节点坐标,进而可通过1 080阶球谐函数方法计算节点扰动引力,最终完成Field模型构建。飞行器发射前,根据飞行任务进行弹道规划,快速获得一条参考弹道。从Field模型数据中读取参考弹道历经的多层网格节点数据,完成Channel模型构建。Field模型数据存储在地面设备中,Channel模型数据存储在弹上。飞行过程中,根据网格节点位置判断当前计算点所在的网格,基于广义延拓逼近理论和节点扰动引力完成当前点扰动引力实时逼近计算。
1.2 子域内的广义延拓逼近算法
将飞行过程中的扰动引力实时逼近考虑为一个三维数值逼近问题。令函数u(x,y,z):R3→R在区域Ω⊂R3上的一组离散数据为
{ui|ui=u(xi,yi,zi),(xi,yi,zi)∈Ω,i=1,2,…,n}.
(2)
在Ω上构造u的一个近似函数U:Ω→R,使其满足U(xi)=ui(i=1,2,…,n)。
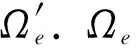
{gj(x,y,z)}={1,x,y,z,x2,y2,z2,xy,xz,yz,x3,y3,
z3,x2y,x2z,xy2,xz2,yz2,y2z,xyz,…}
(3)
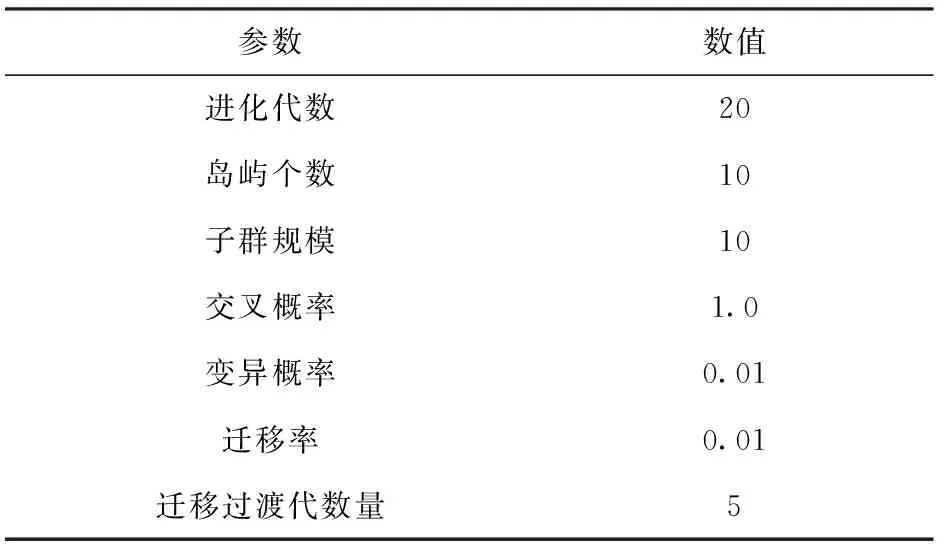
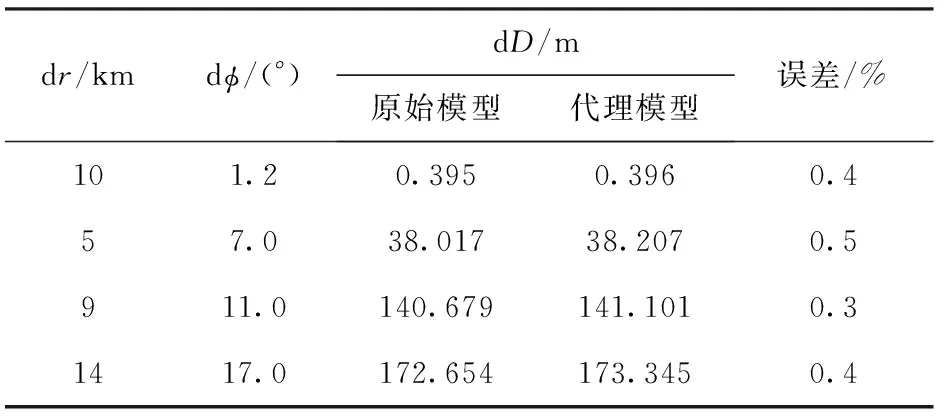
的前t项为插值基函数U(x,y,z),且r (4) 式中:aj(j=1,2,…,t)可由下述问题解出[13] (5) 受弹载计算机能力的限制,重构模型必须兼顾数据存储量、计算速度和重构精度的制约。结合工程应用背景,提出如下两种优化需求:1)给定弹道精度要求,建立存储量最小模型;2)给定存储量要求,建立重构精度最高模型。本节针对上述两类需求,建立基于代理模型的重构模型优化方法。 根据扰动引力重构模型,存储量和重构精度主要取决于如下因素:1)空域剖分参数dr(沿地心、矢径方向的剖分间距)、dλ(沿经度方向的剖分间距)、dφ(沿纬度方向的剖分间距);2)由(4)式决定的三元多项式类的项数t;3)延拓网格节点数s. 弹上数据存储量可以由需存储的节点个数N来表征;重构精度可以用弹道终端位置偏差dD来描述。弹道终端位置偏差dD可由终端纵程偏差dL和终端横程偏差dH计算得到, (6) 则重构模型的优化问题可以描述为如下两类问题: 问题1:给定精度要求,建立存储量最小模型。 目标函数:minN; 待设计变量:dr、dλ、dφ、t、s; 约束条件:dH∈[(dH)min,(dH)max]、dL∈[(dL)min,(dL)max]; 待设计变量取值范围:dr∈[(dr)min,(dr)max]、dλ∈[(dλ)min,(dλ)max]、dφ∈[(dφ)min,(dφ)max]、t∈[tmin,tmax]、s∈[8,smax]。 问题2:给定存储量要求,建立精度最高模型。 目标函数:min dD; 待设计变量:dr、dλ、dφ、t、s; 约束条件:N∈(0,Nmax]; 待设计变量取值范围:dr∈[(dr)min,(dr)max]、dλ∈[(dλ)min,(dλ)max]、dφ∈[(dφ)min,(dφ)max]、t∈[tmin,tmax]、s∈[8,smax]。 求解2.1节描述的优化问题,首先需建立目标函数、待设计变量和约束函数之间的数学模型。由于优化过程通常需通过对计算模型进行多次分析、协调和决策来寻求最优解,针对原始模型进行优化将引入难以容忍的计算量和计算时间,因此必须在满足精度要求前提下构建原始模型的代理模型。本文的代理模型构建过程分为3个步骤:1)开展试验设计,获取弹道仿真基本条件;2)基于仿真条件开展弹道仿真,获取用于训练代理模型的输入、输出对;3)基于训练样本,通过RBF神经网络建立描述输入、输出函数关系的代理模型。基于代理模型的优化流程如图3所示。 基于试验设计结果开展不同计算条件下的弹道仿真,可以获得用于训练代理模型的样本对(Xi,Yi),其中,Xi=(dr,dλ,dφ,t,s),Yi=(N,dD),i=1,2,…,n. 通过RBF神经网络对样本进行训练,可以获得RBF的中心、半径以及隐含层与输出层的权向量,由此可构造节点数N和终端位置偏差dD关于dr、dλ、dφ、t和s的代理模型, (N,dH,dL)=f(dr,dλ,dφ,t,s). (7) 基于RBF神经网络构建代理模型的网络结构见图5. 多岛遗传算法是在传统遗传算法基础上发展起来的一种智能优化算法。该算法将进化群体划分为若干子群(岛屿)。在每个岛屿上对子群体独立地进行选择、交叉、变异等传统遗传算法的操作。此外,该算法定期将一些随机选择的个体迁移到其他岛屿上,以维持群体的多样性。多岛遗传算法在优化过程中,首先基于初值进行优化,初步达到收敛后,通过变异和迁移,在一个新的初值点重新进行遗传操作,由此可以避免局部最优解,达到抑制早熟、提高收敛速度的目的。多岛遗传算法的主要参数设置见表3. 表3 多岛遗传算法参数设置 将第2节提出的扰动引力快速重构方法应用于某考虑两个禁飞区的典型滑翔弹道,校验方法的正确性。弹道仿真条件:1)起点(λ0,φ0)=(0°,0°);2)终点(λe,φe)=(55°,30°);3)圆柱形禁飞区1:半径Rnf1=600 km,中心(λnf1,φnf1,Hnf1)=(20°,20°,100 km);4)圆柱形禁飞区2:半径Rnf2=900 km,中心(λnf2,φnf2,Hnf2)=(45°,20°,100 km)。Field网格和Channel网格如图6所示,节点扰动引力三分量如图7~图9所示。图6表明对于考虑多禁飞区的复杂情况,参考弹道能够成功实现对禁飞区的绕飞,且能够确保被Channel网格完全覆盖。 针对起点为(λ0,φ0)=(0°,0°)、射程为7 000 km、初始方位角为p×10°(p=0,1,…,35)的滑翔弹道开展研究,考察重构方法误差对滑翔弹道终端经度和纬度的影响。重构网格参数为(dr,dλ,dφ)=(10 km,1.2°,1.2°)。在弹道仿真中,将1 080阶球谐函数作为基准弹道,分别与不考虑扰动引力的弹道和快速重构方法获得的弹道进行对比分析,其中扰动引力引起的滑翔弹道终端经度和纬度偏差如图10所示,重构方法误差引起的滑翔弹道终端经度和纬度偏差如图11所示。 对比图10与图11的计算结果可以看出,扰动引力引起的弹道终端最大偏差大于0.1°(约为104m),而当采取(dr,dλ,dφ)=(10 km,1.2°,1.2°)的重构网格参数选取方案时,重构方法误差导致的弹道终端位置偏差不超过0.000 01°(约为1 m)。因此,在适当的网格划分下,重构方法可使弹道终端精度提高104倍。需要注意的是,重构精度与网格参数的选取相关,节点间隔距离越小,重构精度越高,但数据存储量及运算量也相应增大。因此,确定空域剖分方案时需要综合考虑重构精度、数据存储量及运算量的要求。实际上,由于高超声速滑翔飞行器为全程制导飞行器,当滑翔弹道终端位置以一定精度满足中制导与末制导交班条件时,可通过末制导来保证弹道落点精度。一般认为100 m的终端位置约束较为合理,因此在该指标下可适当放宽网格大小以减少弹上存储量。表4给出了不同网格划分参数对应的弹上数据存储量和由扰动引力逼近误差导致的滑翔弹道终端位置偏差。 由表4计算结果可以看出,当采用(dr,dλ,dφ)=(10 km,1.2°,1.2°)的网格划分时,只需在弹上存储158个节点的948个数据,即可将滑翔弹道的终端横程偏差和终端纵程偏差控制在100 m以内,并满足计算精度和弹上存储量的要求。 表4 不同网格划分对应的弹上数据存储量及弹道终端位置偏差 Tab.4 Onboard memory size and terminal positional deviation of glide trajectory for different spatial partitioning scheme 网格参数弹上数据存储量dr/kmdλdϕ(°)节点数数据量终端位置偏差/m101.251831080.11101.527216326.7810215894828.161010112672557.32 将优化方法应用于t、s已知的简化算例,校验方法的正确性。取t=20,s=32. 采用底部为正方形的扁平网格,令dλ=dφ. 设计变量取值范围为drmin=5 km、drmax=15 km、dφmin=1°、dφmax=20°. 在设计变量取值范围内基于最优拉丁超立方试验设计方法进行试验设计,获得样本数为50的试验因素设计结果。针对纵程为6 700 km、初始方位角为90°、再入点和落点位于特大山区(λ0=80°,φ0=42°,λe=147°,φe=19.3°)的弹道开展研究。根据设计得到的试验因素进行弹道仿真,可以获得不同重构参数对应的节点数N和终端位置偏差dD. 基于计算得到的训练样本,采用RBF神经网络方法建立dD和N关于dr和dφ的代理模型,如图12和图13所示。 输入4组随机选择的设计变量,通过将代理模型与原始模型的计算结果进行比较,分析代理模型的拟合精度。代理模型的终端位置偏差拟合误差见表5,代理模型的存储量拟合误差见表6. 表5 代理模型的终端位置偏差拟合误差 由表5和表6可以看出,代理模型具有较高的拟合精度高,终端位置偏差的拟合误差可以控制在0.5%以内,节点数基本无误差。 针对优化问题1,取约束条件为0 m≤dD≤5 m. 采用多岛遗传算法对所建立的代理模型进行优化,经875次计算寻找到满足约束条件的最优网格划分。最优重构模型对应的dr为10.040 km,dφ为3.349°,终端位置偏差为4.570 m,节点数为377. 图14为历次优化计算对应的节点数与终端位置偏差关系示意图。 针对不同弹道终端位置精度要求,分别以0.9 m≤dD≤1 m、9 m≤dD≤10 m、99 m≤dD≤100 m和299 m≤dD≤300 m为约束条件,计算得到不同弹道精度要求下的最优网格划分(见表7). 从表7中可以看出,本文所建立的优化方法可以获得任意给定精度要求下的存储量最小模型。当终端位置偏差限定为0.9~1 m、9~10 m、99~100 m和299~300 m时,最优模型对应的弹上数据存储量仅为468、160、139和125,可以满足弹上数据存储量的要求。 表7 不同重构精度约束下的优化结果 针对优化问题2,取约束条件为N≤400. 采用多岛遗传算法对所建立的代理模型进行优化,经846次计算寻找到满足约束条件的最优网格划分。对应的dr为10.189 km,dφ为3.111°,终端位置偏差为4.030 m,节点数为399. 图15为历次优化计算对应的终端位置偏差与节点数关系示意图。 针对不同弹上数据存储量要求,分别以N≤200、N≤300、N≤500和N≤600为约束条件,计算得到不同节点数要求下的最优网格划分,见表8. 计算结果表明,本文所提出的优化方法可以获得任意给定节点数要求下的精度最高模型。当节点数限定0~200、0~300、0~500和0~600时,最优模型对应的弹道终端位置偏差分别为5.785 m、6.272 m、0.007 m和0.001 m,满足重构精度要求。 表8 不同节点数约束下的优化结果 本文以高超声速滑翔飞行器滑翔段弹道为研究对象,针对飞行过程中扰动引力快速计算问题,提出了一种基于延拓逼近理论的扰动引力快速重构方法。在此基础上,基于最优拉丁超立方试验设计方法和RBF神经网络算法构建了原始模型的代理模型,并通过多岛遗传算法对代理模型进行了优化。仿真结果表明:1)重构方法可适应机动飞行下的复杂环境,在适当的网格划分下,可使弹道终端精度提高104倍;2)代理模型具有较高的拟合精度,终端位置偏差的拟合误差能控制在0.5%以内,节点数基本无误差;3)通过对代理模型进行优化,可以获得任意给定精度要求下的存储量最小模型和任意给定存储量要求下的精度最高模型。考虑到滑翔飞行器大范围侧向机动的特性,可能存在实际飞行弹道超出弹道管道的极端情况,后续可尝试研究针对上述极端情况的重构策略,进一步提升方法的适应性。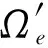
2 重构模型优化算法
2.1 优化问题的数学描述
2.2 基于试验设计和RBF神经网络的代理模型

2.3 基于多岛遗传算法的重构模型优化
3 仿真分析
3.1 重构模型适应性及精度分析

3.2 代理模型拟合精度分析
3.3 模型优化数值仿真


4 结论

