基于泰森多边形服务分区的常规公交站点布局优化

葛 奔，蔡 琳，王 富

武汉工程大学土木工程与建筑学院，湖北 武汉 430074

近年来，随着公交优先发展战略的兴起，城市常规公交由于其具有投资小、见效快、线路易调整及污染少等优点一直都处于快速建设当中，公交站点对于客流的吸引组织作用日渐凸显，公交站点布局是否合理直接影响到乘客公交出行的比例［1］。目前，关于城市常规公交站点布局优化的研究成果主要体现在交通分配、公交客流分配上，关于公交站点服务区的研究成果相对较少，且大都假设站点周边的乘客均匀分布，这种假设产生的结论往往与实际相差较大，因而在实际进行公交站点的布局优化时一般采用人工经验法［2］。公交站点的布局优化需要考虑的因素众多，如人口分布、居住分布、就业分布、道路长度、行车道数、交通量大小等，若需要优化的区域太大，人工经验法很难将需要考虑的因素全部兼顾到，通常只能达到整体指标满足规范要求的层面，导致公交站点在有些区域布设的过于密集而在有些区域又显得格外稀疏的情况出现，满足不了居民实际上的日常出行需求，使高容量的常规公交系统的功能与效率不能充分发挥，从而陷入瓶颈［3］。

在对公交车乘客的乘车习惯进行细致地研究后，发现在需要选择公交出行时，乘客总会优先选择距离自己出发点最近的公交站点，本文假定优化区域内所有乘客都会选择距离自己最近的公交站点出行，这个特性表明各个公交站点所服务的区域其实是一个可以确定的区域，这与“泰森多边形内的点到相应离散点的距离最近”的特性极其相似。因此，本文通过引入“泰森多边形”的概念，将规划区域划分为若干个小区，从站点服务区的特性着手，建立一个基于区域乘客平均步行到站时间的评价模型，在对各个小区逐一进行评价后，对公交分担率不满足要求的小区的公交站点进行调整优化，这样就能在一个比较小的范围内考虑公交站点的布局优化问题，细化公交站点布局优化问题的同时还能增加优化效率，最大程度地满足居民出行需求［4］。

1 基于泰森多边形的服务分区

泰森多边形最早是由荷兰气候学家Thiessen提出来的，Thiessen用每一个泰森多边形内所包含的一个唯一气象站的降雨强度来表示这个多边形区域内的平均降雨强度［5］。将“泰森多边形”的概念引入到公交领域中，从几何角度来看，两公交站点的分界线是两点之间连线的垂直平分线，将全平面分为两个部分，各部分中任何一点与本部分内公交站点的间隔都要比到另一公交站点间隔小。因此，当优化区域内有很多公交站点时，可以将全平面划分为多个包罗“一对”公交站点泰森多边形，那么这个多边形中任何一点都与本区域内公交站点的间隔最近。

由此，总结出公交站点泰森多边形服务区的特性如下：每个泰森多边形服务区内仅含有“一对”公交站点；泰森多边形服务区内的点到相应公交站点的距离最近；位于泰森多边形边界上的点到其两边公交站点的距离相等。

对于泰森多边形的建立，目前已有比较成熟的算法，引入其中一个较为实用的生成程序的算法如下所示：输入点集读取，去除点集中的重复点，计算MBR（最小外包矩形）；在远距离点集MBR的四角加入4个额外点；Delaunay三角部分；将Delaunay三角形转化为泰森多边形；将生成的泰森多边形裁切到合适的范围内；输出最终结果［6］。

图1 泰森多边形制作流程图Fig.1 Flowchart of making Voronoi Diagram

因此，在对优化区域进行公交站点的泰森多边形服务分区时，只需找出现状区域内公交站点的具体坐标，然后确定区内离散点的坐标，将其输入至算法中，优化区域就会被划分为许多多边形区域，这些多边形区域就是各个离散点的服务区域。

2 基于泰森多边形服务小区的优化方法

2.1 离散点坐标的确定

本文模型是建立在区域内的乘客优先选择离出发点最近的公交站点的基础上，这里所指的公交站点是一对（包含来和去），取2个公交站点连线的中点作为离散点的具体坐标，对于某些区域只设有来或去的单向公交站点，可先将此站点坐标作为离散点坐标，若由此站点建立的泰森多变形面积过小，则根据实际情况选择将其与周边多边形区域进行合并［7］。

2.2 评价指标的确定

居民出发点距离公交站台的距离越近，乘客乘坐公交就会越方便［8］，本文主要通过泰森多边形区域内乘客到站的平均步行时间来评价此区域的公交服务水平，以区域内公交出行的比例作为指导公交场站布局优化的主要指标，且乘客步行到站时间与下车后离站时间同步行路程与道路条件等有关系，不受其他因素干扰［9］。

2.3 评价模型的建立

根据实际情况可知，区域内乘客的到站时间与乘客出行速度成正比，与路程成反比，即：

式中：ti为第i个乘客到达离散点所需的时间；Vi为第i个乘客到达离散点的平均速度，步行速度取5 km/h；Li为第i个乘客步行至离散点最近的路程。

假设多边形区域内共有n个乘客选择公交出行，那么此区域乘客平均步行到站时间为：

模型中考虑的影响因子主要有服务区域内人口数量、土地开发强度、道路条件等［10］。杨晓飞在《公交服务半径及服务水平研究》中指出，居民出发点距离公交站点越近，乘坐公交就越方便，区域公交出行分担率相对高，其通过大量的居民出行调查得出，居民选择公交出行的比例与其到公交站点的时间呈对数关系［11］，建立公交出行率和步行时间的关系如下：

式（3）：α、β为影响系数，与区域发展水平有关；t为步行至公交站点所需的时间；λ为区内公交分担率。

2.4 优化方法

在优化区域分区完成后对每个服务小区进行细致地分析，根据计算可以得出这个服务区的乘客平均步行到站时间。首先，对多边形区域内部的乘客发生源做细致的划分，根据其用地性质和占地面积用以估算各发生源乘客的数量；然后，统计各个发生源步行至公交站点的时间；在得到区域内各发生源乘客的数量和步行至公交站点的时间后，根据公式（2）计算得出服务区的乘客平均步行到站时间。

其中乘客数量乘客平均步行到站时间最小为

式中：Sj为第j个发生源的占地面积；γj为第j个发生源地块的容积率；μj为第j个发生源的发生率，根据同类建筑调查总结后得出；tj为第j个发生源步行至公交站点的时间。

在计算得出区域内乘客平均步行到站时间后，将数据带入公式（3）可得出服务区内公交分担率，若达到优化目标则定位该区域为公交建成区，若没达到优化目标则定位为公交拓展区。在公交拓展区域需要对其中的站点位置进行优化调整，通过建立候选车站集合，选择满足优化目标且使乘客平均步行到站时间最小的候选站点作为该服务区公交站点的最终站点［12］。对于候选公交站点的选址需遵循以下几个原则：

1）公交候选车站的位置应优先选择乘客主要的发生源，例如城市的轨道站点、商业中心、交通枢纽、学校、医院、行政单位、居民小区、长途客运站、火车站等。

2）为了方便乘客乘车与换乘，候选站点优先选择交叉路口附近，但需要对公交车辆的延误时间、对交叉口通行能力与交通流的干扰以及对行人安全性的影响进行充分论证［13］。

3）如果在高等级和低等级道路相交的交叉口上设站，其拐弯线路的站点应优先选择设在高等级道路上。

4）常规公交市区线与郊区线的中间停靠站站距分别为500 m～600 m，800 m～1 000 m，常规公交大站快车的市区线与郊区线的站距分别为1 500 m～2 000 m，1 500 m～2 500 m。

5）居民出行乘坐公交的最大出行距离不超过1 000 m，相邻多边形服务区内两离散点的500 m覆盖范围重复率不得超过20%［14］。

3 案例分析

以武汉市东湖高新技术开发区为研究对象，在对东湖高新技术开发区的常规公交站点位置进行实地调查后，可以确定311个离散点的具体坐标，通过建立泰森多边形将东湖高新技术开发区划分为311个公交站点服务小区，根据上文所提到的优化方法，在对每一个服务区进行仔细的分析计算后，以武汉市打造公交都市提出的45%公交出行分担率为目标，将分担率大于45%的服务区定位为建成区，分担率小于45%的服务区定位为拓展区［15］，建立东湖高新技术开发区各服务小区评价图如图2所示。

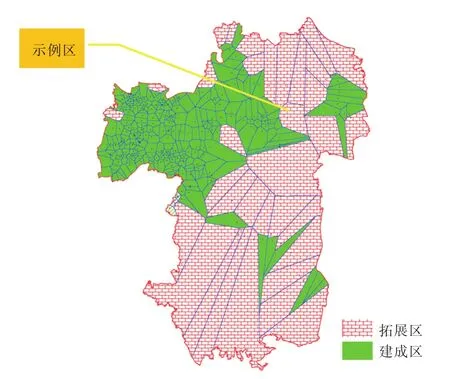
图2 服务小区评价图Fig.2 Evaluation map of service area

由于篇幅限制，本文只选取高新大道畈里熊服务小区作为示例，其他小区皆可类比计算出评价指标。结合畈里熊服务小区的用地性质可知，服务小区内用地以农林用地为主，其次是科研教育用地，根据服务区的用地性质确定区域内的10个发生源，调查每一个发生源的占地面积、容积率及步行至离散点的时间，通过计算可以得到这个服务区的平均步行到站时间及公交出行分担率，公交站点和发生源分布服务区现状如图3（a）所示，经济技术指标如表1所示。

图3 畈里熊服务小区：（a）优化前，（b）优化后Fig.3 Fish Bear Serving Cell：（a）before optimization，（b）after optimization

表1 优化前畈里熊服务小区经济技术指标Tab.1 Economic and technical indexes in Fish Bear Serving Cell before optimization

对武汉东湖高新技术开发区的居民进行问卷调查，调查结果显示95%的乘客认为去公交站点最大的步行时间要控制在12 min以内，建立东湖高新技术开发区乘客公交出行的比例与到站时间的关系如下：

将乘客数量和步行到站时间代入式（2），计算得到畈里熊服务小区平均步行到站时间约为7.37 min，将小区平均步行到站时间代入式（6）后可得畈里熊服务小区的公交出行分担率为28%，这个分担率与武汉打造公交都市提出的45%公交出行分担率的目标显然不符，属于公交拓展区。若想在此区域达到45%的公交出行目标，需考虑居民出行需求量及发生源距离公交站点的距离，以公交候选站点选址原则为依据建立公交站点候选集，选择使区域乘客平均步行到站时间最小的候选站点，代入式（6），仍不满足优化目标。在对表1中8、9、10发生源进行实地勘探之后，选择新增一对公交站点如图3（b）所示，则此服务区1～7号发生源步行到站时间不变，变化的只有8、9、10号发生源，优化后该小区经济技术指标如表2所示。

同样地，将优化后的乘客数量和步行到站时间代入式（2），计算得到畈里熊服务小区平均步行到站时间约为4.98 min，公交出行分担率为46%，达到优化目标，则方案可行。

表2 优化后畈里熊服务小区经济技术指标Tab.2 Economic and technical indexes in Fish Bear Serving Cell after optimization

4 结 语

本文将“泰森多边形”的概念引入到公交领域，在客观上反映了居民出行特性与公交站点布局优化的紧密联系：

1）不同于传统分区方法，本文以泰森多边形区域作为每一组公交站点的服务区域，完成对优化区域的分区；

2）引入了制作泰森多边形的高效算法；

3）基于区域内乘客平均步行到站时间建立了评价模型；

4）通过调查数据确定了公交出行比例与步行到站时间的关系；

5）根据评价结果将优化区域分为建成区和拓展区，通过最终评价指标来指导拓展区公交站点的布局优化，形成了一套完整的公交场站布局优化方法。