矢量偶极孤子在光折变非均匀非线性介质中的传输特性

元绍霏

(中国电子科技集团公司第四十六研究所 天津300200)

1 光折变效应机理

光孤子被发现始于人们对声孤子逐渐深入的探讨。孤子在自然界中有数不胜数的种类，其中有一种就是我们所要研究的空间孤子。它表示光束在介质中传播时，将受到非线性效应作用，与此同时也有衍射效应作用，当这两种作用能够相互平衡时，我们可以断定该光束能够稳定传播在该种介质中形成空间孤子[1]。光孤子是一种不会改变外形的脉冲，在长距离传输的状态下，不同频率的一束光脉冲在同种介质中的传播速度也不同，并且在光纤中发生色散从而脉宽变宽。

本文讨论两束偶极光束在光折变介质中的传输过程，并且讨论其在非均匀非线性的作用下形成偶极空间孤子对的可能性。

2 理论推导与数值模拟

2.1 理论模型

带输运模型有4个方程可用来描述光折变现象。

速率方程：

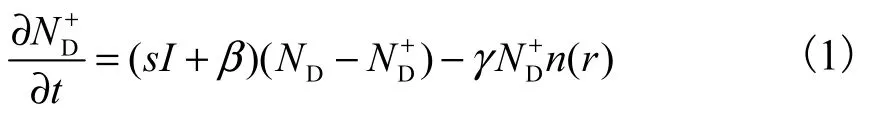
自由电子连续性方程：

电流方程：

泊松方程：

光折变材料导致的折射率变化可写为[2]：

式中：n0表示介质本底折射率；reff表示有效电光系数；E表示空间电荷场，其方程为：

光折变晶体的局域自散焦非线性可以通过掺杂Fe、Cu等金属离子实现。假定此时的折射率为：

光束在介质中的传播特性由非线性薛定谔方程描述：

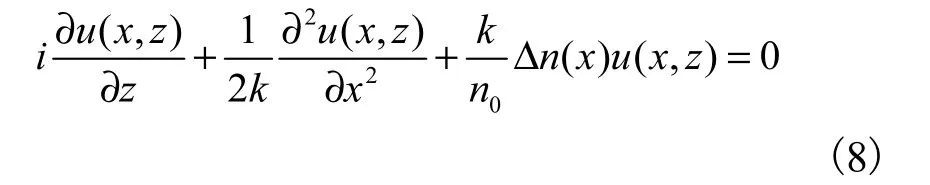
0λ表示入射光束的波长。

如果考虑在外加电场作用下，上述方程归一化后可得到以下方程：

式中：U (X,Z)为归一化光束振幅。

如果考虑两束非相干光束传播在该介质中，可得到如下耦合方程：

基于此耦合方程，对于非相干耦合孤子对的形成，我们可以这样假设：

代入上式耦合方程组，可得到解耦的单一方程：

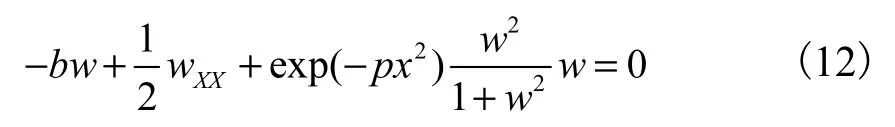
2.2 非均匀自聚焦非线性介质中偶极光束传播特性

利用分步傅里叶方法数值解耦合非线性薛定谔方程组，通过改变入射光束的振幅和宽度数值，研究了孤子脉冲在非均匀自聚焦非线性介质中的传输特性。由图1可知，孤子可以稳定传播在非均匀自聚焦介质中(图中 x轴为衍射方向，z轴为传播方向，I表示光束光强。下图同。)

由图2可知，在非均匀自散焦非线性介质中，不同倍振幅入射时矢量光束先会聚再衍射发散，形成准周期传播特性。

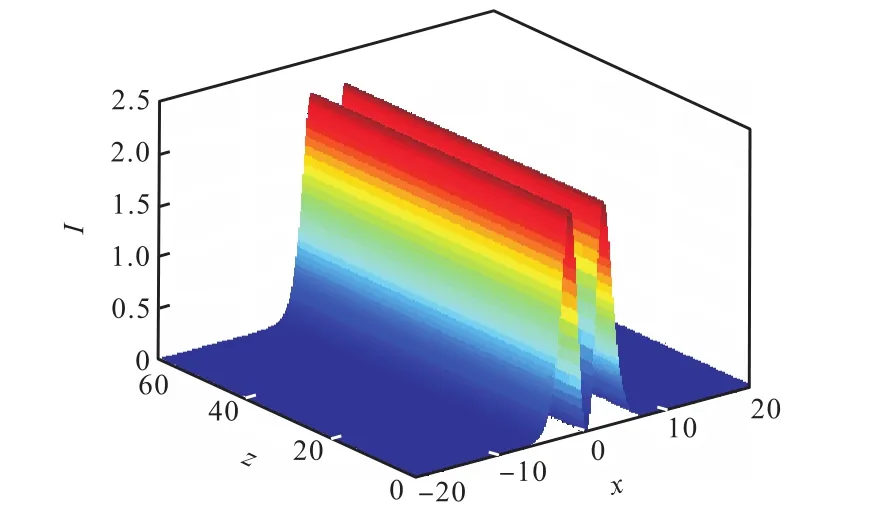
图1 当b=0.2、p=0.1时，在非均匀自聚焦非线性介质中，矢量偶极孤子对的典型传播特性Fig.1 Typical propagation characteristics of vector dipole soliton pairs in non-homogeneous selffocusing nonlinear media when b = 0.2,p=0.1

图2 在非均匀自散焦非线性介质中，1.5倍振幅入射时矢量孤子的典型传播特性Fig.2 Typical propagation characteristics of vector solitons in non-homogeneous self-focusing nonlinear media with an incident amplitude of 1.5 times

由图3可知，在非均匀自散焦非线性介质中矢量光束衍射发散后会聚，形成准周期传播特性。

图3 在非均匀自散焦非线性介质中，0.8倍振幅入射时矢量孤子的典型传播特性Fig.3 Typical propagation characteristics of vector solitons in non-homogeneous self-focusing nonlinear media with an incident amplitude of 0.8 time

由图4可知，在非均匀自散焦非线性介质中矢量光束先吸引会聚，再衍射发散，光强逐渐减小。

由图5可知，在非均匀自散焦非线性介质中矢量光束衍射发散传播，光强减小。

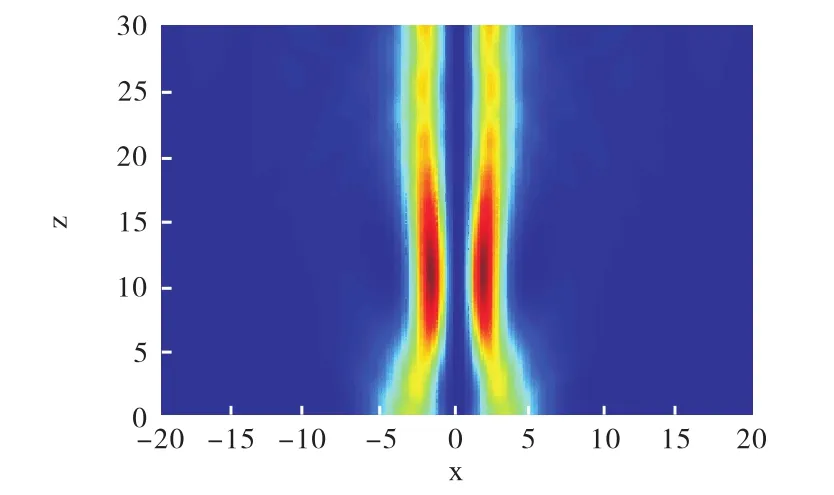
图4 在非均匀自散焦非线性介质中，束宽较小入射时矢量孤子的典型传播特性Fig.4 Typical propagation characteristics of vector solitons in non-homogeneous self-focusing nonlinear media with small incident beam width

图5 在非均匀自散焦非线性介质中，束宽较大入射时矢量孤子的典型传播特性Fig.5 Typical propagation characteristics of vector solitons in non-homogeneous self-focusing nonlinear media with large incident beam width

3 结 论

本文介绍了光折变效应的含义及其理论模型，给出描述光束传播的方程，得出了最简单的耦合矢量孤子对，并且通过改变入射光束的振幅和宽度数值模拟了该孤子对的形成及其传输过程。结果表明，当入射光束的轮廓与孤子轮廓相匹配时，将形成稳定传播的矢量偶极孤子对。