基于复杂网络的交通系统的动态管理*

范申民

（商洛学院 商洛 726000）

1 引言

随着交通运输业发展的日趋成熟，在一个城市区域可能有多种对外交通方式在此交汇，并形成大型旅客集散中心和转换中心，从而逐步演化为新的综合交通枢纽［1］。近年来，随着区域之间生产要素的快速流动，以高速铁路客运站、城市轨道站点为代表的综合交通枢纽成为了城市建设的热点［2～4］。综合交通枢纽是城市对外和对内交通衔接的重要节点，是城市和区域客运系统的重要组成部分，其对客流的疏散，对提高区域客运交通网络运转效率、缓解城市交通拥堵等具有重要作用［5］。然而许多现代综合交通枢纽是在原来老的枢纽设施基础上改造升级而来，使得综合交通枢纽的改造成为旧城改造，城市更新的重要组成部分［6］。这样一来，因项目的改造升级，增加开发强度引来的新的客流可能将导致新的交通拥堵问题。近年来，综合交通枢纽与城市功能的叠加发展已引起了学术界的关注，其中优化路网结构，提高道路服务水平是缓解项目因开发强度提高导致的城市中心区交通压力难以疏解的重要手段，也是综合交通枢纽项目开发需要解决的关键问题之一［7］。因此，构建路网结构的评价模型，加强路网结构的定量评价有助于对规划前后道路服务水平形成正确判断，从而提高交通枢纽区域综合开发决策的科学性。

本文尝试采用沙坪坝综合交通枢纽区域数据，借助复杂网络和空间句法的理论与方法构建定量分析模型，对项目实施前后其影响区域范围内交通网络性能进行评价，为综合交通枢纽工程改造提供决策参考。具体研究内容包括：1）依据复杂网络的理论对项目实施改造前的交通网络现状进行评价；2）对沙坪坝铁路枢纽综合改造工程规划道路进行分析，评估项目实施后道路网络结构与性能的变化；3）对现状和规划的交通网络状况进行对比分析。

2 理论与方法

下面分别从点（节点）、线（网络本身）和面（被网络分割后的空间）等的联通特性来构建定量分析模型，评价区域道路的联通状态。

2.1 节点评价模型

本文选择度值（KI）、通达指数、可达性三参数对路网节点进行评价。度表示与某节点直接相连的边的数量。度是节点重要性的度量，表明点在局域位置的上重要性［8］，其计算公式见式（1）。

式中，Ki表示节点i的度，eij表示节点i与 j直接相连的边。

通达指数是网路中从一个顶点到其他所有顶点的最短路径，也是对节点重要性的度量，表明点在全局位置的上重要性，通达指数公式见式（2）。通达指数大小与该点的通达度好坏成正比［9］。度和通达指数公式相似，但含义不同。

式中，Ai表示顶点i在网络中的通达指数；Dij顶点i到研究区域任意顶点 j的最短距离。可达性指节点的连通性，可用不对称性值的倒数来表示。深度值是空间句法中最重要的概念之一，它主要表达空间转换的次数，而不是指实际距离［10］。从一节点到另一节点的最短路程（即最少步数）就是这两个节点间的深度值dij。平均深度值指系统中某个节点到其他所有节点的最短路程（即最少步数）的平均值，即称为该节点的平均深度值。由于平均深度值的大小在很大程度上决定于系统中节点的数目［11］。为剔除系统中元素数量的干扰，P.Steadman通过改进计算方法将其标准化得到相对不对称值［12］，其计算公式见式（3）。

式中，AIi表示相对不对称值，RAi为i点的不对称性值，其计算公式见式（4）。

式中，MDi为点i的平均深度值，n为关系图解中所有的点的个数，其计算公式见式（5）。

式中，dij为两点间最短路程，n含义与式（4）式同。

2.2 网络评价模型

选择网络连接度、分散指数、全局网络效率三参数对路网特性进行评价。网络连接度表示交通网络的发达程度，常用β指数表示。β指数为边的数量与顶点数量比，其计算公式见式（6）。

式中，β指交通网的连接度；E指交通网的边的数量；V指交通网中顶点的数量。

分散指数是用来衡量网络系统中总的通达程度与联系水平。分散指数越小，说明网络内部的联系水平越高，通达性越好。分散指数计算公式见式（7）。

式中，C指分散指数；Dij表示顶点i到顶点 j的最短距离。

全局网络效率是指网络中所有节点对之间距离倒数之和的平均值［13］。网络效率越髙，网络信息流通越容易［14］。城市交通网络的整体连通性可以用全局效率来说明，全局效率范围在0～1之间，当全局效率为0时，表示整个交通网络的所有节点之间都不相连，或者交通网络处于全部拥堵状态，造成所有重要节点之间都是孤立不相连的，网络的可靠性也是最差的。当全局效率为1时，说明城市交通网络中所有的重要节点都是相连的，因此，全局效率越接近1，其连通的可靠性就越接近1，其计算公式见式（8）。式中，E表示全局网络效率值；N表示网络中节点的数目，其中εij指网络中的节点i与节点 j两点间的效率，网络效率是用来衡量网络中信息传递有效程度的指标，它用网络中任意两节点对之间距离的倒数来表示，其计算公式见式（9）。

式中，dij表示节点i与节点 j之间的距离。和一般的路径定义不同，在复杂网络中，定义两个节点的距离为连接这两个节点的最短路径的边数。

2.3 空间联通性评价模型

这里用全局整合度表示空间联通性。全局整合度考察一个空间与其他所有空间的关系，数值越大表示该空间在整体空间系统中的位置越便捷［15］，其计算公式见式（10）。

式中，Rn表示i点（或空间）的全局整合度；RRAi指实际相对不对称性指数，其计算公式见式（11）。

式中，RAi为i点（或空间）的不对称性值；Dn来自于钻石模型，表示集成度标准化值，其计算公式见式（12）。

式中，n表示关系图中节点个数，Dn含义与式（11）相同。

3 现状与规划路网方案

本文研究所用的一部分规划和现状数据来自重庆市规划局和2012年度的《沙坪坝铁路枢纽综合改造工程可研报告》。一部分地图数据来自百度地图和现场调研补充。经过矢量化［16］等数据处理后，构建了用于分析的ArcGIS基础数据库。

3.1 项目影响区域“二环八射”路网方案

为便于分析计算，本研究把复杂的交通网络转化为简单的路网图来分析项目区附近的路网状况。简化原则为：通行量较少的道路或胡同忽略不计；禁止车辆通行的商业步行街忽略不计。简化后的沙坪坝地区主要路网结构，见图1。

“二环八射”是沙坪坝区域“十一五”规划期末形成的道路格局，其中一环指三峡广场环道，二环是杨公桥→梨树湾→天星桥→天马路→小龙坎→龙泉路→沙杨路→杨公桥形成的循环道，7条放射状道路为渝碚路、沙坪坝正街、汉渝路、上土湾路、石小路、天星桥正街、站西路。与此同时，站东路向东延伸至沙滨路，站西路向西延伸至大学城，形成“二环八射”的路网格局。

图1 枢纽改造工程影响区域“二环八射”现状道路分布图

3.2 项目影响区域“三环十射”路网规划方案

根据《沙坪坝区交通“二环八射”规划》（2011-2015年），沙坪坝中心区域将形成“三环十射”的道路网络。过去几年里，沙坪坝在“两环八射”道路网络的基础上，新增了多条道路构成沙坪坝“三环十射”的道路网络，使得道路交通的连接更为复杂，交叉路口也随之增加，沙坪坝地区道路交通的结构特征随之变化。

沙坪坝地区新增的“射线”都在沙坪坝商圈以外，三环也是在二环以外进行扩建。见图2。

图2 沙坪坝枢纽改造工程影响区域“三环十射”规划道路分布

“三环十射”中一环由小新街、南开隧道、站东路构成；二环由站南路、龙泉路、沙中路、沙杨路、杨公桥、重师路构成，其中重师路由重师、建专校区穿过；三环由杨梨路、天梨路、天马路、平顶山路、滨江路、磁童路、杨双路构成。一射线指渝碚路，由磁童路口至双碑、北碚；二射线起于建大后门，由建大穿过，从建大大门往北至滨江路；三射线由南开隧道、沙磁路至磁器口；四射线从三角碑由汉渝路至石门大桥；五射线起于滨江路平顶山路接口，由西至东渝中区；六射线由小龙坎、土湾路至红岩村、渝中区方向；七射线由天马路下穿石小路接红岩村大桥；八射线指石小路，由小龙坎至石桥铺；九射线由凤天路南北向凤鸣山、二郎地区；十射线由天星桥、高滩岩正街至凤鸣山、新桥地区。

3.3 项目路网改造方案

根据枢纽改造方案（已由重庆市发改委以渝发改交［2012］1275号文批准建设）（2013年4月开工，计划竣工日期2018年8月），项目的修建需对沙坪坝区域的道路进行改造。根据总的交通组织方案制定其中的各个道路方案。共含新建及改建道路8条，分别为站西、站东路（改建）、站西、站东路下穿道（新建）、天陈路下穿道（新建）、天陈路北段（改建）、天陈路南段（改建）、站南路（新建）、东连接路（新建）、西连接路（新建），见图3。

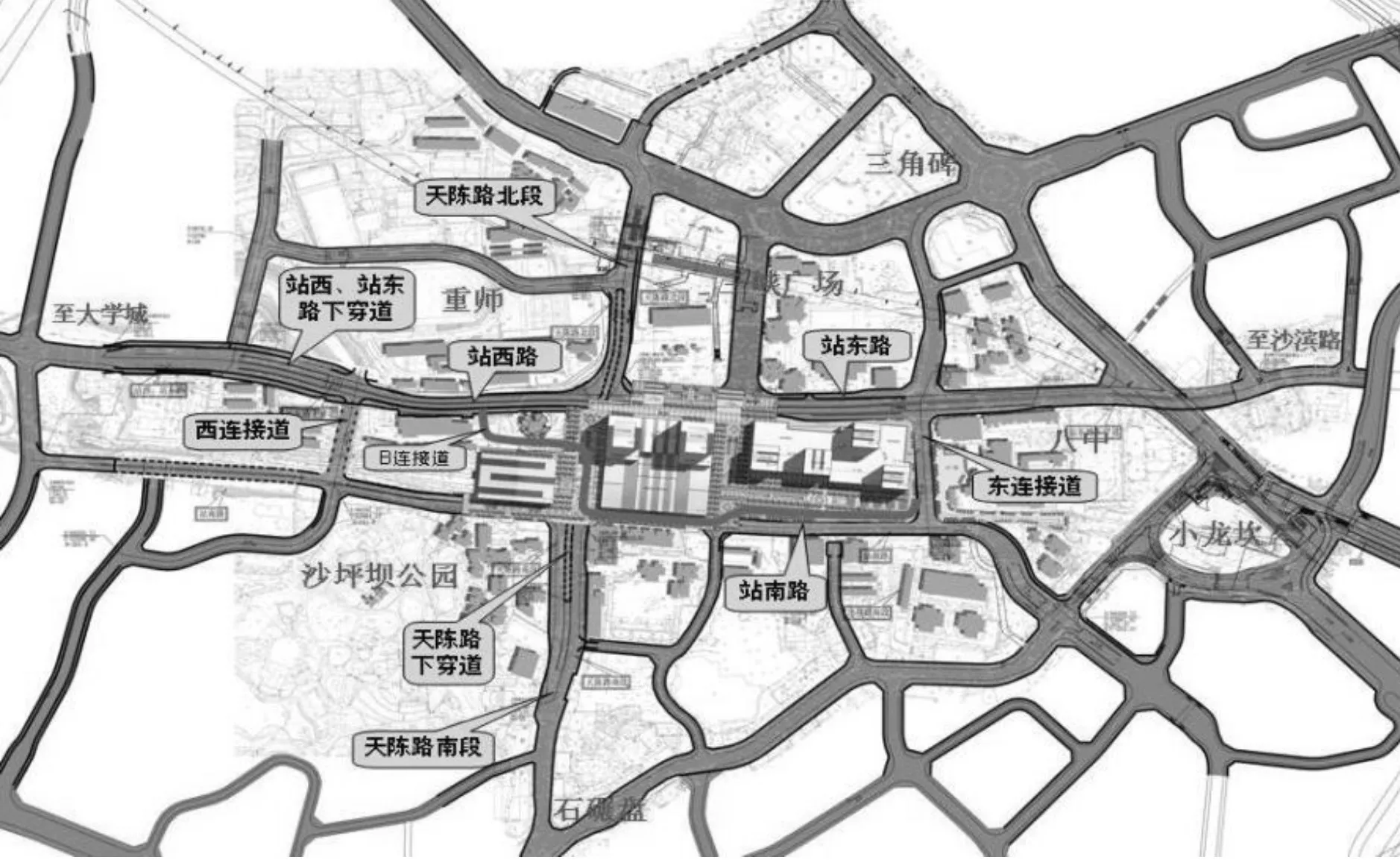
图3 项目区道路改造方案

站西、站东路配合上盖广场下沉，改建起于站西路与清溪路交叉口东侧，止于站东路与华宇支路交叉口东侧，改建范围全长1.14km。站西、站东路下穿道位于天陈路下穿道下一层，起于站西路，止于站东路与华宇支路交叉口东侧，道路全长0.962km。站南路起于清溪路，向东分别与西连接路、天陈路、东连接路平交后，转向东南下穿小龙坎正街，设一简易立交，终点接入小凤路。东连接路是连接站南路与站东路的支路，位于重庆八中西侧，道路全长183m；西连接路是连接站南路与站西路的支路，位于重师南门南侧，道路全长149m。天陈路是连接陈家湾、南开下穿道以及天星桥正街的城市次干路，本次改建范围全长720m。下穿道起于天陈路北段，向南分别下穿天陈路北段与站西站东路的T形平交口、沙坪坝火车站、天陈路南段与站南路的T形平交口之后，接入天陈路南段，见图4。

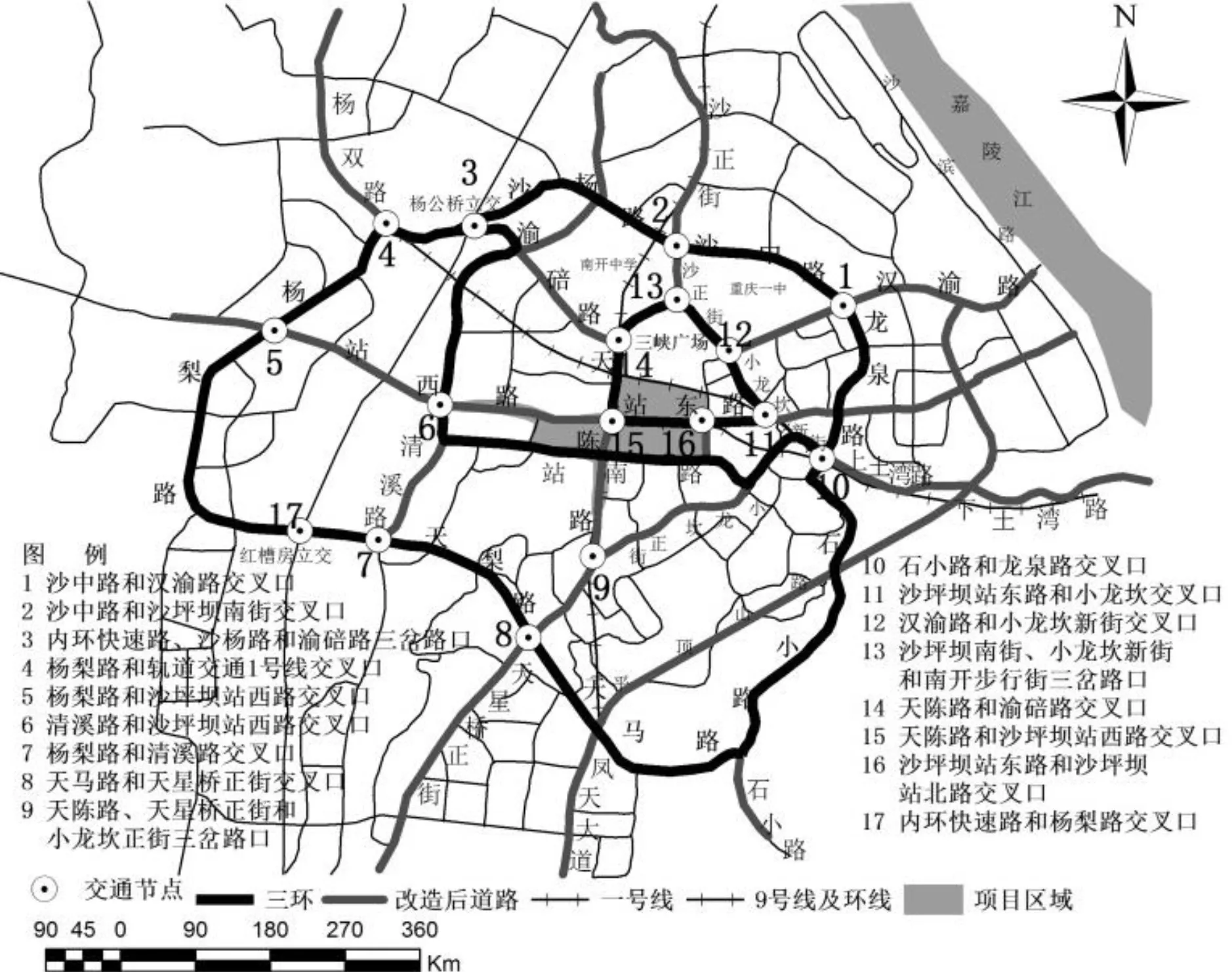
图4 沙坪坝综合枢纽改造工程规划图

4 比较分析

依次采用上述计算模型对路网现状（二环八射）、规划方案（三环十射）和枢纽改造方案三种方案的路网特征进行定量计算，在此基础上进行比较分析。

4.1 网络各节点参数比较

依据式（1），计算节点的度，根据式（2）算出各个节点的通达指数，根据式（3）算出各个节点的可达性，具体结果见表1。

对“二环八射”的道路现状而言，根据度值计算发现，节点3、11、15的度较高，即表明在该网络中，3、11、15节点是关键节点，在局域网中居于重要地位，其中11节点度达到5，最高。计算结果表明，搞好3、11、15等节点的交通疏散，特别是项目所在地11的交通改造至关重要。

根据通达指数计算发现，11节点通达指数最小，其次是3、4点。通达指数与区域节点数量有关，可达性则剔除系统中元素数量的干扰。从可达性计算结果来看，11可达性最高，其次是3、4、15。

对于“三环十射”的规划路网结构来说，节点3、6、10、11的重要性最高，度值达到5，需要对这几个节点的交通情况更加关注，以免局部拥堵所造成整个交通网络瘫痪的状况。“三环十射”的路网规划使得3、6、10等节点的度有所提高，这说明这些节点的连通性得到了增加。

表1 网络各节点参数比较表

根据通达指数计算结果，大部分（12个）节点的通达指数有所减小，说明这些节点的通达度有所提高。与此对应的可达性指数有所增加。

对于枢纽改造方案而言，由于项目改造工程的建立和道路的新建，大多数节点的通达度和连通性相对规划来说得到进一步提高，其中节点6的重要性再次被提高，度值在“三环十射”的路网规划的基础上提高到6，其次节点11提高到7，成为整个交通网络中最重要的节点。其次9、14、15节点也有提高。

相对于“三环十射”方案，可达性平均提高了11.44%，除了1、16、17节点外，其它节点的可达性都有不同程度的提高。相对于“二环八射”的路网结构，平均提高26.74，其中节点6的可达性提高了108.81%，10、11分别提高了50.09%和45.33%。

4.2 网络结构特征比较

分别从网络连接度、分散指数、全局网络效率等方面对三种方案（现状、规划、枢纽改造方案）进行比较。根据式（6）算出网络连接度，根据式（7）算出分散指数，根据式（8）算出全局网络效率。不同情形下的网络拓扑图，见图5、6、7。

从理论上讲，对于17个点来说最连通的理想状况为任意两点两两相连，在这种情况下，网络连接度的理论最优值是8，分散指数为272，全局网络效率为1，见表2。

图5 现状路网结构（2012年）

图6 规划路网结构（2020年）

图7 项目开发改进后的路网结构（2020年）

表2 网络结构特征比较

从表2可以看出，虽然经过规划和改进，但是每个指标和理想值还是有很大的差距。由于现实的道路条件和经济状况并不允许修建如此多的道路，因此，理想状况并不可能达到，但可以作为评价的参考。其中，连接度表示交通网络的发达程度，从三种方案比较来看，网络连接度总体是上升的。现状道路网络连接度为1.59，三环十射的规划道路网络连接度为1.76，项目改造工程将使得网络连接度提高到1.94。

全局网络效率越接近1，其连通的可靠性就越接近1。从三种方案比较来看，全局效率总体是上升的，但离理想水平还有一定的差距。现状道路全局网络效率为0.51，三环十射的规划道路（2020年）全局网络效率为0.54，改进后的规划方案全局网络效率0.57。总体来看，三峡广场周围的交通网络效率不高，与理想值还有一定差距。

分散指数越小，说明网络内部的联系水平越高，通达性越好。从三种方案比较来看，分散指数总体是下降的，分别为640，602和572。

4.3 三种方案的空间联通性比较

项目改造前空间布局具有以下特点：1）火车站将北侧的商业区和南侧的居住区分割，北侧繁华，南侧萧条；2）开敞空间被分割为零星空间，商业区距离开敞空间如沙坪公园，不能为人流疏散提供方便；3）用地结构不合理，各用地类型的比例不协调，特别是开敞空间少，缺少像欧洲的大车站周边辅助以一定区域的开敞空间。

这里采用空间句法方法，对开发前后的城市空间整合度进行定量评价。分别对不同情形下被道路分割的街区空间进行编号，街区与街区相通则空间编号抽象为拓扑连接。对项目影响区域的空间进行分析如图8、9。

图8 项目影响区域拓扑图（2012年）

根据式（7）算出分散指数。根据式（10）算出全局整合度，见表3。

表3 全局整合度计算结果比较

从计算结果来看，项目改造前后街区的全局整合度明显改善，整合度平均提高了99.85%。提高程度最高的是8区，整合度绝对值提高了2.05，其次是4、5区，全局整合度绝对值分别提高了1.26和1.24。另外，除6街区外，其它街区都有所提高。从相对值来看，除6、7区外，其他区域都提高了45%以上，4区和8区提高了190%以上。这说明原火车站的铁路阻断了附近各个区域的联系，而新交通枢纽的建立使得空间整合度大大提高，各个区间的连通度也有了明显加强，见图10、11。

图10 项目影响空间区域图（现状）

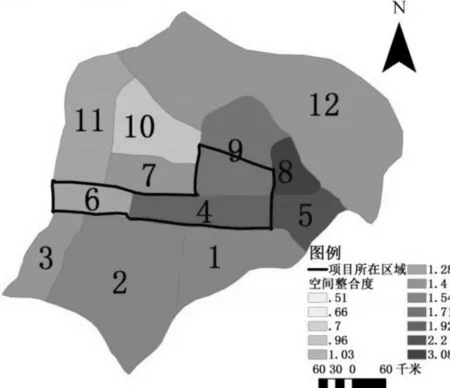
图11 项目影响空间区域图（规划）

5 结语

本研究采用复杂网络和空间句法方法构建路网特征的定量评价模型，并对项目开发前后交通网络性能进行了评价，研究表明通过枢纽改造方案的实施，项目周边道路节点、路网结构和空间整合等交通网络性能得到了一定程度的改善。本研究仅对项目实施前后道路网络拓扑结构的变化进行了评估，未来将进一步采集区域交通流量数据，通过项目实施前后道路通畅程度（道路交通压力）的变化，评估项目对未来交通产生影响，以便找到相应的应对方案。此外，在道路网络不断完善的情况下，节点数量也会发生变化，为了进行对比分析，本研究在分析节点特征和网络结构整体特征时仅关注了现有节点情况，新增节点没有纳入考虑范畴，这些都有待后面进一步完善。