10 MW推进电机的抗冲击能力研究

彭 攀

(上海电气集团上海电机厂有限公司，上海 200240)

0 引言

动力系统是舰船的一个重要子系统。船舶动力系统在各种工况下均可连续、可靠、高质量运行，它不仅是保证舰船发挥其效能的必要条件，也是保证舰船生命力和重要设备生命力的必要条件。因此，提高动力系统(主要是推进式异步电动机)在船体遭受波浪、水下爆炸等冲击载荷作用下的抗冲击能力，就相应提高了动力系统的稳定性，同时提高了整个舰船和重要设备的生命力[1]。

由于电机系统进行冲击试验投入人力大、费用高，测试所获得的数据有限等诸多限制，人们普遍趋向于采用低成本、高性能和高仿真的有限元数值模拟仿真方法。当前，这类仿真方法主要是利用有限元分析软件，比如ANSYS、LS-DYNA、NASTRA、HYPERMESH等[2-3]。

ANSYS由于其强大的流固耦合功能和多学科兼容性而得到了广泛的应用。本文系统地分析了某异步推进电动机在遭受冲击载荷作用下的动力特性，结合当前ANSYS软件，建立了相应的有限元仿真模型，完整地叙述了仿真计算方法和分析过程，并给出了类似情况相应的分析方法和模型修改意见。

1 问题描述

型号YBKS10000-12，10 MW异步推进电机的工作环境为大型船舶，稳定转速200 r/min。电机由基座左右各一块底板通过铆钉连接在船体上，转子由两支撑轴承支撑。其3D模型如图1所示。假定水底某方向突然发生爆炸，对船体产生一个加速度(通过计算我们定该加速度为15 g)，由于电机固定在船体上，因而电机本身也受到同样的加速度。考虑电机在这个冲击环境下工作的稳定性，我们要求：转子本体产生的最大变形不超过气隙，以免发生“扫膛”现象；同时，电机地脚螺栓不能断裂，以免电机整体和船体分离。

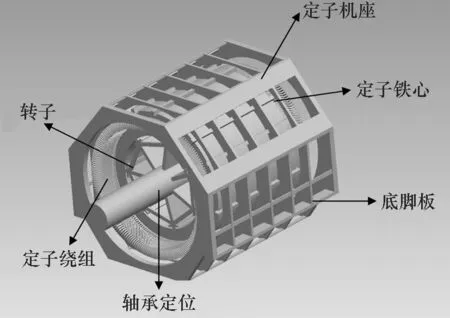
图1 电机三维模型

2 基本尺寸和材料参数

主要控制尺寸如表1所示。

表1 控制尺寸 单位：mm

取用材料参数如表2所示。

表2 材料参数

3 分析思路

由于模态变形的不对称性以及整机结构的特殊性，考虑简化忽略一些不确定性因素，因此先采用整机三维CAD建模，对于套在轴上与轴同时旋转的部件如护环、导条、挡风环等，首先计算出这些部件的质量，并求得相应的转动惯量将其施加对应的轴段上，等效为圆截面[4]，再在ANSYS中对其拓扑结构进行简化和修改，删除倒角和小尺寸孔洞，以消除应力集中效应，提高计算精度。其转子最终的FEM模型如图2所示，该模型含有12 080个单元，32 266个节点。由于对电机整体进行瞬态动力学分析需要耗费较大的计算资源，需要考虑的因素有以下几点：

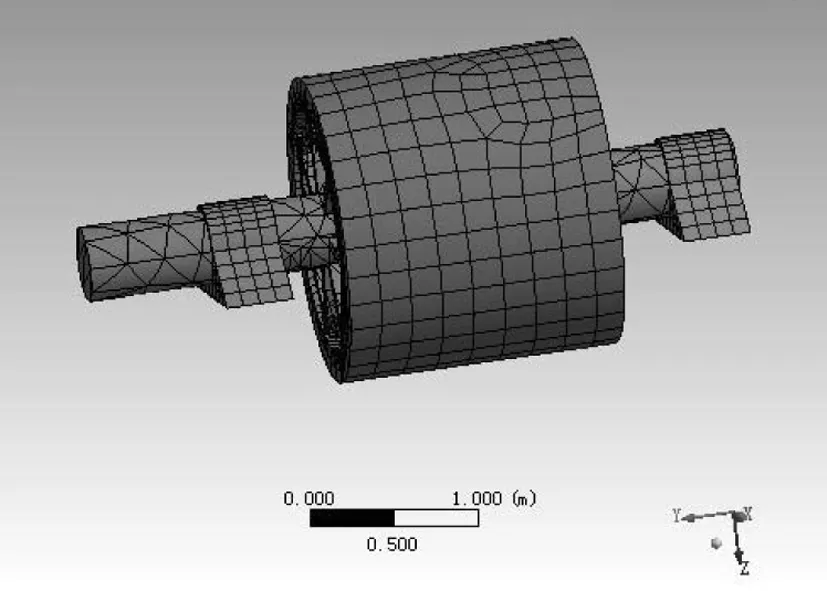
图2 转子系统的FEM模型

(1) 高度非线性(接触，碰撞，间隙刚度)；

(2) 稳态到瞬态的转变；

(3) 时间积分。

为了准确分析计算，我们必须对可能发生的情况有一个充分的了解。因此我们还需要确定的因素有：

(1) 间隙刚度(试算为3.24×1012Pa)；

(2) 接触正则惩罚系数和阻尼(默认)，忽略质量阻尼α，阻尼比β取为5；

(3) 积分时间(分别对每个零部件进行模态分析，取加权平均模态确定各自积分时间，分别取最大和最小时间为积分时间，并结合接触刚度确定ITS)；

(4) 冲击载荷作用时间(0.5 s)；

(5) 单边磁拉力(以稳态运行15 g的加速度下产生的径向位移所对应的磁拉力与“扫膛”零界位移对应的磁拉力的加权平均值计12 289.5 N)。

通过反复的研究分析，我们确认了如下基本思路：

单个零件模态分析—转子部分稳态、瞬态分析—将转子计算结果施加在基座部分求其稳态、瞬态分析—形成分析报告。

底板Q345钢材料屈服强度按345 MPa，许用应力为其70%，不高于241.5 MPa；轴15MnMoV屈服强度大于370 MPa，许用应力为其70%，不高于259 MPa；转子本体最大径向位移7 mm，计为许用径向位移。

4 有限元计算结果

4.1 固有频率及积分时间的计算

图3a、3b、3c分别是机座的一、二、三阶模态(1.33 Hz、2.84 Hz、4.13 Hz)；图4a、4b分别是转子的一、二阶固有频率(2.79 Hz、6.14 Hz)；分别求取机座和转子的加权固有频率分别为3.7 Hz和7.24 Hz，由此计算得到最大和最小积分时间0.138 s和0.267 s。转子的工作转速为200 r/min，其工作频率值fg=3.33 Hz，而(fg-f1)/fg×100%=16.2%，(f2-fg)/fg×100%=84.4%，均满足工程上避开15%的要求，此外转子的其他各阶固有频率都已避开了激振源频率，且无倍频关系存在，所以从振动角度来看，转子不会产生共振，转子结构是安全的[5]。

4.2 稳态运行时力学性能的计算

图5a、5b为转子在未受冲击载荷时的等效应力和总的位移。载荷条件为：转速200 r/min，重力加速度9.81 kg/m2。可以看出此时系统的最大等效应力发生在轴承处，大小为35.73 MPa，而转子本体的最大位移为0.02 mm(远小于气隙的10%，即0.7 mm)，转子系统是稳定的。图6a、6b为转子在受15 g冲击载荷时的等效应力和总的位移，转速200 r/min，重力加速度-147.15 kg/m2。图6c为轴在受15 g冲击载荷时的等效应力。可以看出此时转子系统的最大等效应力发生在轴承处， 大小为464.7 MPa，而转子本体的最大位移为0.18 mm(远小于气隙的10%，即0.7 mm)，计算安全系数为3.8，转子系统仍然是稳定的。由图6c可知轴的最大等效应力发生在轴承作用位置处，大小约为40 MPa(远小于许用应力259 MPa)，轴也是稳定的。

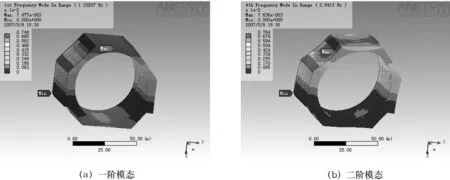
图3 机座的固有频率

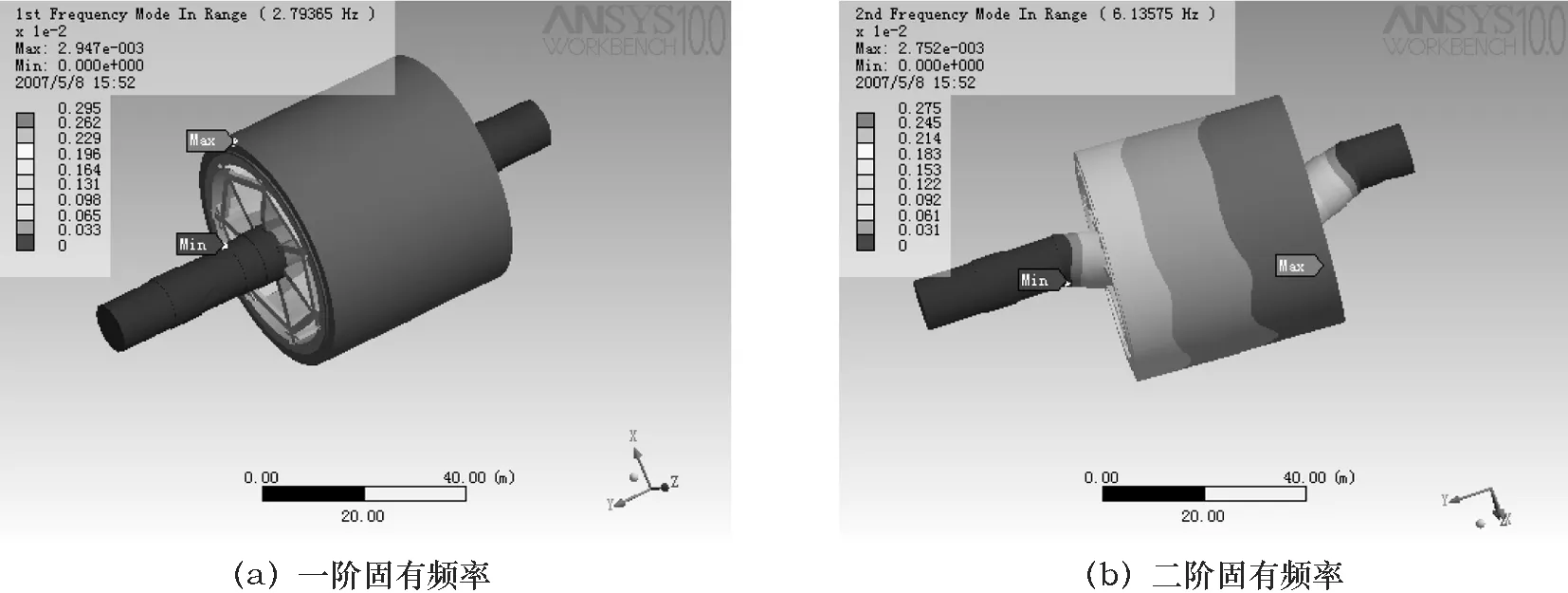
图4 转子的固有频率

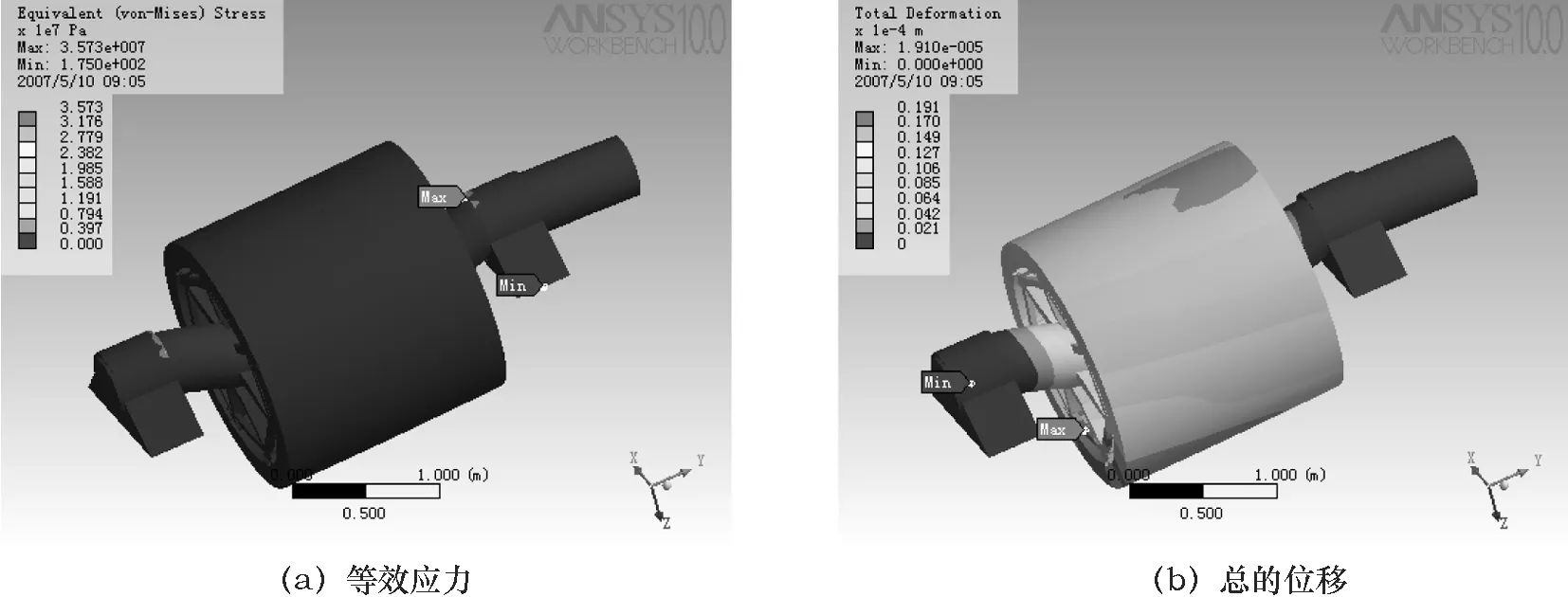
图5 未受冲击载荷时转子的等效应力和总的位移

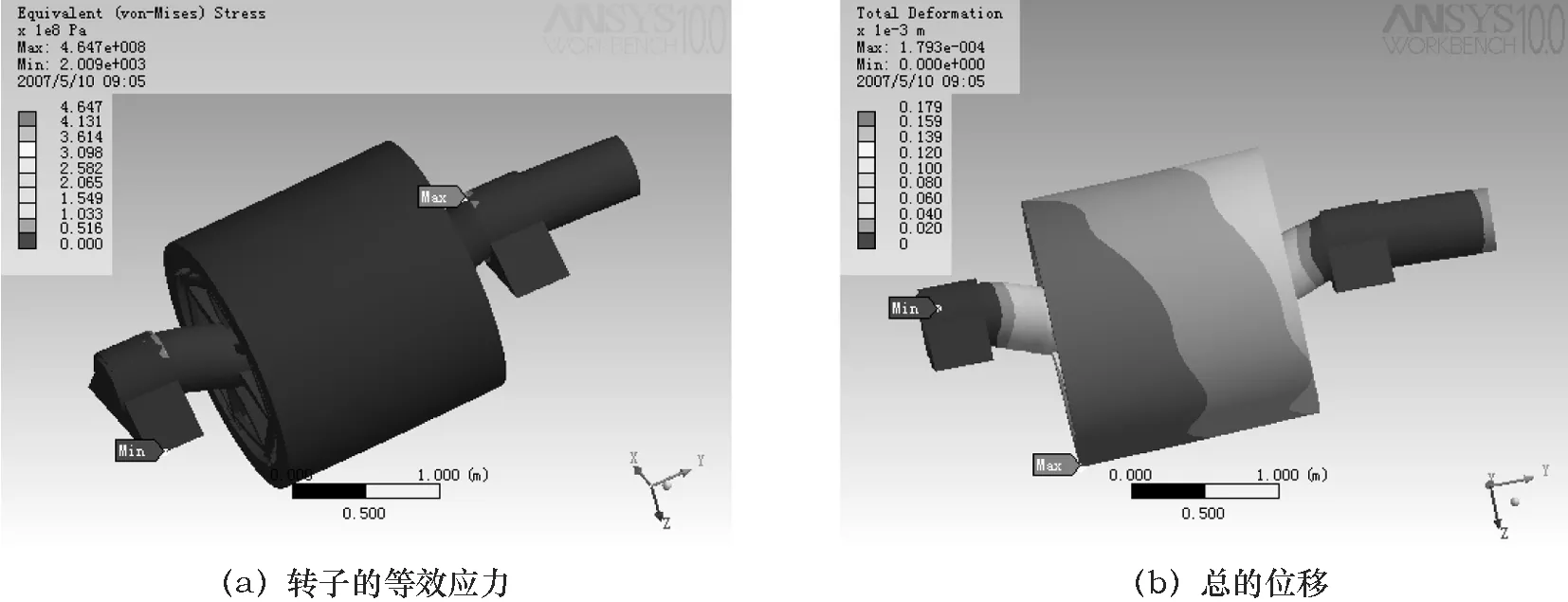
图6 15 g载荷作用下转子的等效应力、总的位移和轴的等效应力

4.3 瞬态运行时力学性能的计算

将轴承处的等效应力施加在基座上，并对其施加15 g冲击载荷得到机座在受15 g冲击载荷时的等效应力和总的变形如图7a、7b所示。可以看出最大等效应力发生在轴承偏右一侧，其值约为560 MPa，如图8所示，强度远超一般合金钢，设计时应考虑修改相应材料。分析原因为：转子本体很大(直径1 830 mm，导致产生很大惯性)，同时转子本体全部质量都作用在轴承上，在冲击载荷作用下，转子对轴承产生一个很大的冲击附加值，又由于转子顺时针转动对该冲击有偏转作用，从而导致最大应力发生在轴承偏右处。图9为最大等效应力附近单元应力变化。

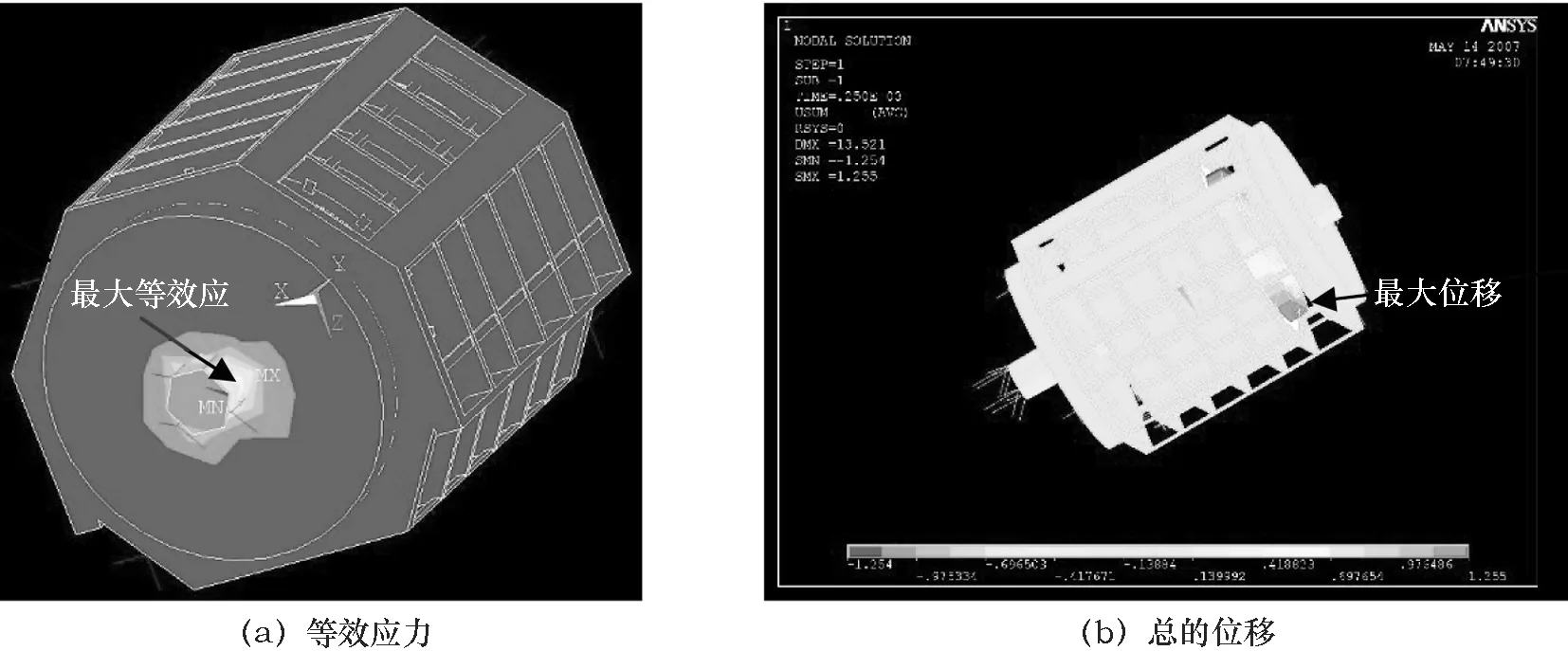
图7 受冲击载荷时系统的等效应力和总的位移

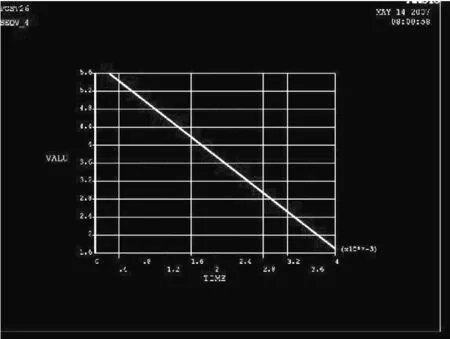
图8 轴承最大应力处等效应力变化

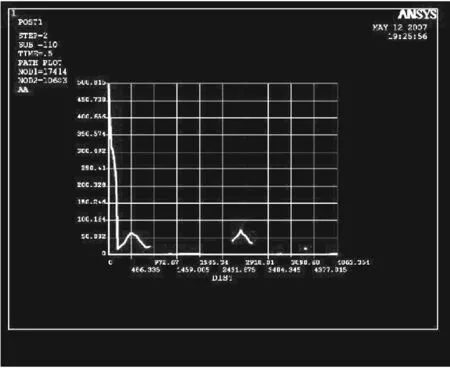
图9 最大等效应力附近单元应力变化

图10为转子本体在冲击作用下最大位移处单元的位移变化(对应于图7b)，可知在冲击的整个过程中，转子本体的位移一直在增大，最大位移为2.25 mm(小于7 mm)，不致“扫膛”，因此转子本体的设计满足工况，设计可行。

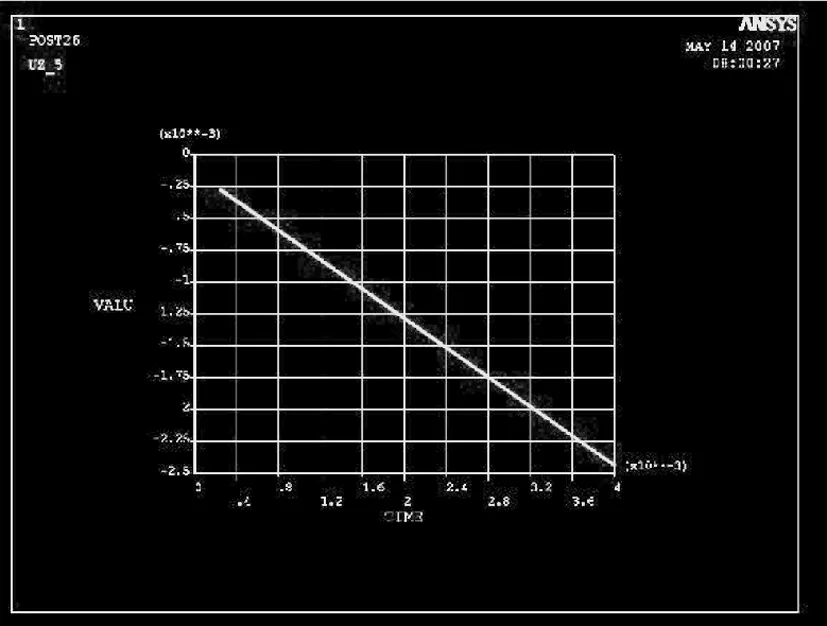
图10 转子本体最大位移处位移变化

底板沿轴向方向上有代表性的节点的位移及其对应的最大等效应力，可以看出节点最大位移发生在传动端的另外一边沿轴向距离挡板约为250 mm处，值为2.64 mm；此处对应的最大等效应力为248 MPa(大于Q345钢的70%的屈服强度241.5 MPa，但是小于15MnMoV的70%屈服强度259 MPa)，建议设计时在此处采用15MnMoV的铆钉，或者70%屈服强度大于238 MPa的材料。

5 结论

(1) 转子系统的各阶固有频率均满足工程上避开激振源频率15%的要求，且无倍频关系存在，所以从振动角度来看，转子不会产生共振，转子结构是安全的。

(2) 转子系统在重力加速度和15 g的冲击载荷下，潜在危险点发生在轴承处，最大等效应力为464.7MPa；而转子本体的最大位移为0.18 mm(小于气隙的10%，即0.7 mm)，安全系数3.8，转子系统仍然是稳定的。

(3) 15 g瞬态冲击载荷的作用下，系统的最大等效应力发生在轴承偏右一侧，其值约为560 MPa，强度远超一般合金钢，设计时应考虑修改相应材料。

(4) 在底板设计的材料选择时，建议采用15MnMoV的铆钉，或者70%屈服强度大于238 MPa的材料。