永磁同步电机自适应鲁棒电流预测控制

于 霜，储建华

(1．苏州工业职业技术学院，苏州215104;2．南京航空航天大学，南京210016)

0 引言

永磁同步电机交流伺服系统中，电流环决定了系统的暂态和稳态性能，如何构造一个稳定性高、动态性能良好且控制精度高的电流环成为高性能伺服控制的关键。因此，具有优良暂态性的电流预测控制成为伺服控制的研究热点。电流预测控制精度依赖准确电机模型参数，预测过程须对参数扰动偏差进行充分考虑。

鉴于PWM预测算法优良的动态性能，众多国内外学者致力于改进传统PWM预测算法，通过结合扰动观测［1］、鲁棒控制［2－3］、模型参考自适应等方法，将PWM预测算法引入到电流预测控制中，加强对参数扰动的鲁棒性。文献［1］基于无差拍思想推出预测方程，用Luenberger观测器观测的电流构造鲁棒预测电流控制算法。文献［2］通过引入两个电流权系数，使系统在模型参数不准确时依然能保持大范围稳定，文献［3］在文献［2］鲁棒性算法的基础上，利用电流误差在线调节磁链参数以及增加积分环节以消除d，q轴电流静差。Siami M等人对传统预测电流控制进行延伸，不仅降低了电流纹波，也提高了系统对参数不确定性的鲁棒性［4］。Lin C K等人给出一种电流差分检测技术驱动系统，利用对应于不同开关状态逆变器的电流差异提高电流跟踪性能［5－6］。文献［7］结合广义预测控制理论和扩张状态观测器，提出新型转速跟踪控制方法，通过对扰动量的补偿，提高了系统鲁棒性。Ayad A等人提出了准Z源逆变器的直接模型电流预测控制策略，推导出精确捕获逆变器所有工作模式的离散时间模型。采用分支绑定策略以及移动阻塞方案，有效解决了潜在的计算优化问题［8］。Wang B等人在建模中考虑了由参数变化引起的干扰，采用离散的Luenberger观测器估计定子电流和系统扰动，其中设计的观测器增益的选择是系统控制带宽和鲁棒性之间的折中，此方案消除了系统扰动引起的稳态电流误差［9］。为优化具有模型参数不匹配和控制延迟的永磁同步电机系统的电流控制性能，Zhang X提出一种用于永磁同步电机驱动系统的改进无节拍预测电流控制算法，分析了当存在参数不匹配时常规预测电流控制的性能，提出基于滑模指数逼近定律的定子电流和扰动观测器，同时预测定子电流和由实时参数失配引起的系统干扰［10］。Türker T提出了一种新的离散时间鲁棒预测电流控制器，为了提高鲁棒性，将离散时间积分项加到死区电流预测中［11］。Carpiuc S C开发了一种基于Lyapunov理论超前预测控制律，使用二次约束的多元近似来降低复杂度，通过多参数线性规划获得分段控制律，使用二次Lyapunov函数设计状态和扰动观测器，以保证估计误差系统的渐近稳定性［12］。

考虑到永磁同步电机定子电阻、电感以及转子磁链等内部参数的摄动问题，本文基于电机离散模型设计Luenberger电流控制器，在此基础上引入自适应观测器观测电机d，q轴系统扰动，用以实时补偿电流预测控制器的输出电压，提高电流预测的鲁棒性以及控制精度。实验结果表明，本文的自适应鲁棒电流预测控制算法对电流预测精度高，对电机电阻、电感以及转子磁链摄动有着较强的鲁棒性。

1 自适应电流预测控制

将定子电阻、电感以及转子磁链等内部参数摄动归结为永磁同步电机d，q轴电压的系统总扰动，即系统总扰动dd，dq表达式:

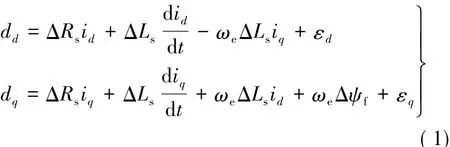
式中:ΔRs，ΔLs，Δψf为电机定子电阻、电感以及转子磁链的参数扰动;εd，εq为未知动态。

相应的，将内部参数摄动引起的系统总扰动引入d，q轴电压方程，得到:

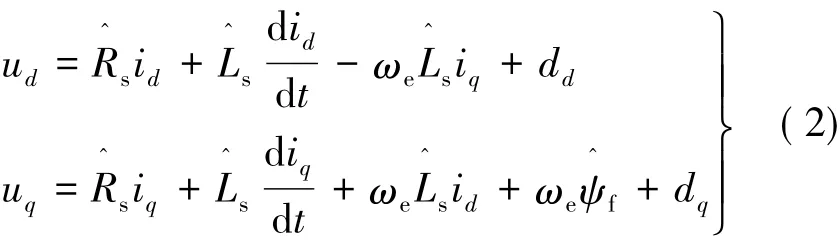
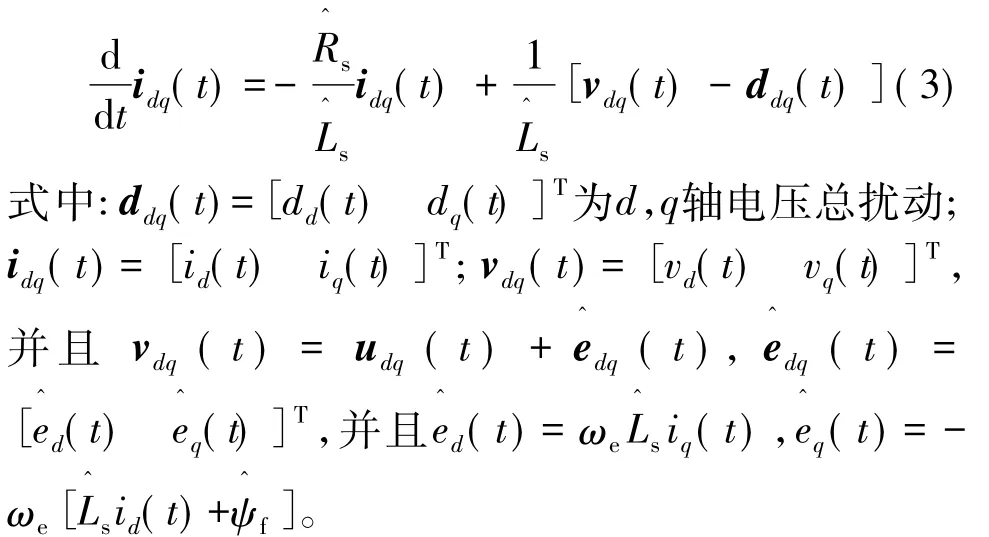
将式(3)进行离散化处理，得到离散模型:

为有效解决离散化处理带来的滞后问题，将式(4)模型超前处理，即令:

相应的电流控制率给定:

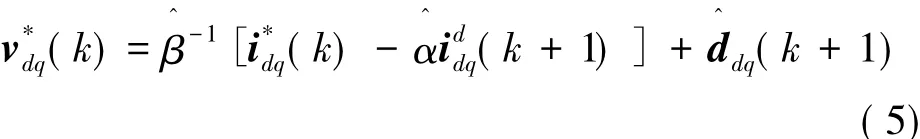
根据式(5)，kT时刻的鲁棒无差拍预测电流控制率给定依赖(k+1)T时刻的d，q轴系统扰动观测。假设kT时刻的d，q轴系统扰动已知，则(k+1)T时刻的d，q轴系统扰动可由拉格朗日插值公式得出:

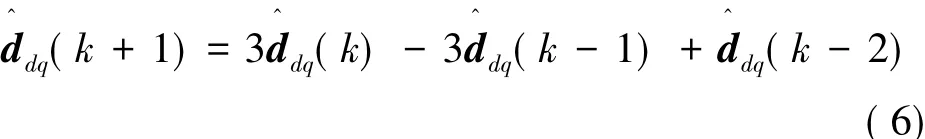
采用Luenberger状态观测器对(k+1)T时刻的电流进行观测，其差分方程表示:

2 自适应扰动观测器设计

根据式(3)构造扰动观测器参考模型:

由edq(t)≡0可知，=0，将edq(t)≡0和q(t)=0代入式(10)，得到=0，即除 edq(t)=0 且=0 外，edq(t)=0和 d～dq(t)≠0不是受扰运动解，当 edq(t)≠0或 d～dq(t) ≠ 0 时，V·(edq(t)，。 ，(11)， 恒不为零 另外 根据式 当

根据上述分析，按照式(13)扰动观测器的自适应率，可使得观测系统大范围渐进稳定，即当t→!时，edq(t)→0。此外，为保证式(9)可调模型有界稳定，系统扰动观测需满足其中ddqmin，ddqmax为系统扰动的最小值和最大值。

3 自适应扰动观测器收敛性分析

将式(10)电流误差状态方程进行离散化，得到:

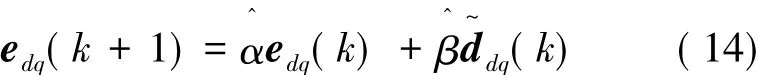
为保证式(14)电流误差系统的稳定性，构造Lyapunov函数:

根据离散域内的Lyapunov稳定性理论可知，为使得式(14)电流误差系统大范围渐进稳定，Lyapunov函数需满足:

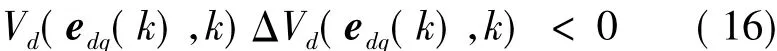
式中: ΔVd(edq(k)，k)=Vd(edq(k+1)，k+1) －Vd(edq(k)，k)为相邻采样时刻的Lyapunov函数值变化。

根据式(15)可知，Lyapunov函数Vd(edq(k)，k)为正定函数，即Vd(edq(k)，k)＞0，若要使式(16)成立，需满足 ΔVd(edq(k)，k) ＜ 0。

根据式(13)，扰动观测器自适应率可离散化为:

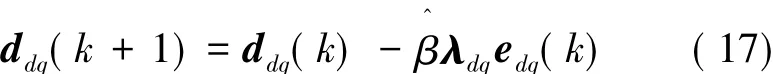
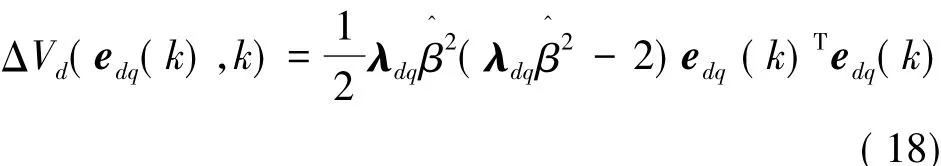
式(18)中，由于 λdq＞ 0，故，又对于任意的，因此若要使得＜ 0，仅需满足即0 ＜时，电流误差系统渐进稳定，即自适应扰动观测器轴系统扰动观测收敛于实际值。

4 实验验证与分析

在永磁同步电机交流调速实验平台上，对本文的自适应鲁棒电流预测控制算法进行了实验验证。将该电流预测控制算法与传统PI控制算法作对比，相应的实验电机参数:额定功率为460 W，额定转速为1050 r/min，额定转矩为4．2 N·m，定子电阻、电感分别为 0．015 Ω 和 66．2 μH ，转子磁链给定为 0．006 18 Wb ，极对数为 4。

图1为定子电阻扰动下的两类电流控制对比曲线。给定电机非线性增大的转矩工况，两类控制器中定子电阻均给定为标称值的0．5倍。图1(a)为通过PI控制算法得到的q轴电流参考值、反馈值对比曲线以及相应的跟踪误差曲线，其q轴电流跟踪误差随着给定转矩的增大而增大。图1(b)考虑定子电阻扰动对电流稳态误差的影响，将电阻扰动造成的d，q轴系统扰动观测用于实时补偿电流预测控制器的输出电压，整个转矩非线性增大的过程中，电流反馈值严格跟随参考值，稳态电流误差始终在零附近。

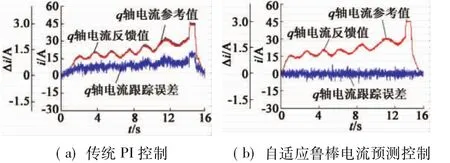
图1 定子电阻扰动下的两类电流控制对比

图2 为定子电感扰动下的两类电流控制对比曲线。给定电机正弦变化转矩工况，两类控制器中定子电感均给定为标称值的1．5倍。图2(a)为通过PI控制算法得到的q轴电流参考值和反馈值波形对比曲线，其q轴电流反馈值存在明显的振荡，从而导致实际输出转矩存在高频抖动。对比图2(b)，考虑定子电感扰动对电流稳态误差的影响，连续变化的转矩工况下电机交轴电流均能精确跟随目标给定值，稳态电流误差始终为零，整个过程电机输出转矩一直处于平滑状态。

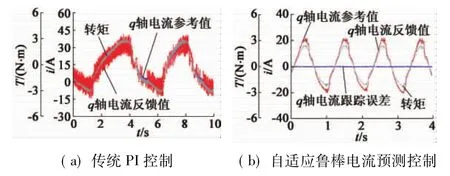
图2 定子电感扰动下的两类电流控制对比

图3 给出转子磁链扰动下的两类电流控制对比曲线。给定电机正弦变化转速工况，两类控制器中转子磁链均给定为标称值的1．5倍。图3(a)为通过PI控制算法得到的q轴电流参考值、反馈值对比曲线以及相应的跟踪误差曲线，其q轴电流存在明显的稳态误差，误差随电机转速的增加而增加。图3(b)考虑转子磁链扰动对电流稳态误差的影响，无论转速高低，稳态电流误差始终为零。

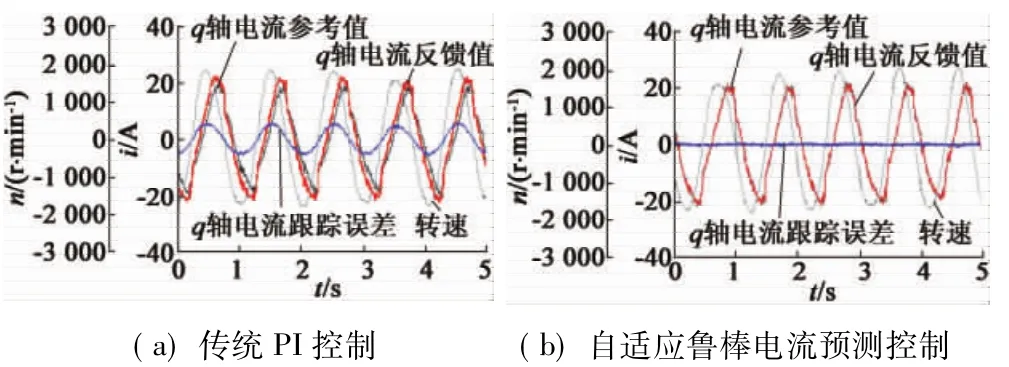
图3 转子磁链扰动下的两类电流控制对比

5 结语

本文针对传统永磁同步电机电流预测控制易受电机参数摄动影响的问题，提出一种考虑电机内部参数摄动的自适应鲁棒电流预测控制算法，采用Luenberger观测器预测电机电流，结合Lyapunov稳定性理论设计自适应扰动观测器观测d，q轴系统扰动，用以实时补偿电流预测控制器的输出电压，提高电流预测的鲁棒性以及控制精度。

以一台460 W永磁同步电机为实验对象，研究基于本文新型算法下的电机电流响应波形，考虑电机定子电阻、电感以及转子磁链等扰动因素对电机输出交轴电流的影响。实验结果表明，本文的自适应鲁棒电流预测控制算法电流预测精度高，对电机内部参数如电阻、电感以及转子磁链摄动有着较强的鲁棒性。