基于响应面法的外转子永磁电机齿槽转矩抑制

杜晓彬，黄开胜，谭耿锐，黄 信

(广东工业大学，广州510006)

0 引言

外转子永磁同步电机与传统的内转子电机在结构上相反，该结构转子在外围，而定子与转轴在内，有利于风机的轮毂、风叶等部件方便地安装在转子上，每极能产生较大的磁通，转矩密度较高，且定子的槽口向外，电枢绕组的绕制也较内转子电机要简单，适用于机械绕制。由于外转子永磁电机拥有质量和体积较小、效率高、结构简单、安装维护方便的特点，被广泛应用于管道通风，压缩制冷、净化空调等方面［1－3］。

然而，在外转子永磁同步电机中，由于定子槽与磁钢的相互作用，导致电机内磁场储能的变化，不可避免会产生齿槽转矩，影响了空载气隙磁场波形的正弦性，导致电机的输出转矩产生波动，引起电机振动和噪声［4－5］。故在电机设计过程中，削弱齿槽转矩是很有必要的，一直以来也是国内外专家学者研究的热点之一。

通过在电机定子上开辅助槽的方式来抑制齿槽转矩是一种简单可行的方法，其效果相当于增加了定子槽数，从而改变了极槽配合，选择合适的辅助槽个数、槽口宽度、深度以及辅助槽位置可以有效地抑制齿槽转矩［6－10］。传统的研究方法是通过单变量实验的方法来研究，即在辅助槽个数、槽口宽度、深度以及辅助槽位置四个影响辅助槽的变量中，固定三个变量，选取其中一个变量，采用不同的步长进行实验，研究单一变量与齿槽转矩的关系，从而确定最优的单一变量取值，并用同样的方法逐步确定其他变量。由于该种方法实验次数比较多，且实验时不能考虑各个变量之间的交互作用，本文采用响应面法(以下简称RSM)与粒子群(以下简称PSO)算法相结合的方式进行研究。通过Box－Behnken设计安排不同因素变量水平的实验组合，利用有限元软件仿真得到不同组合下的齿槽转矩幅值，采用多维二次模型进行拟合，得到响应函数，并分析了变量之间的交互作用。将响应函数作为适应度函数，通过PSO模型求取最优组合，结果表明，通过RSM－PSO模型的方法，能有效抑制确定最优辅助槽参数，从而达到抑制齿槽转矩的目的。

1 基于辅助槽的永磁电机齿槽转矩分析

1．1 外转子永磁同步电机齿槽转矩表达式

根据表贴式外转子永磁同步电机运行原理，在电机中，假设定子铁心磁导率无穷大，永磁材料的磁导率等于空气磁导率，不考虑饱和情况，则当不斜槽时，齿槽转矩的傅里叶表达式:

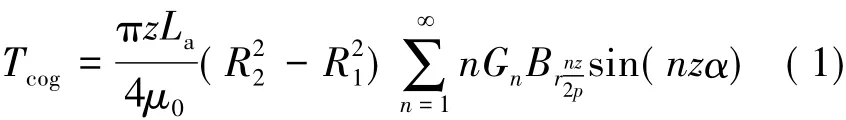
式中:z为电枢槽数;La为铁心长度;R1，R2分别为定子外径、转子内径的半径，n为使nz/2p为整数的整数。其中，的傅里叶展开式系数表达式:

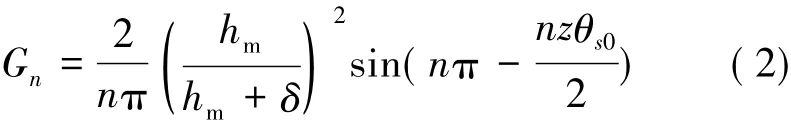
式中:θs0为用弧度表示的槽口宽;hm为磁钢充磁方向长度;δ为有效气隙长度。

1．2 定子齿冠开辅助槽削弱齿槽转矩分析

当在定子齿冠上开辅助槽时，对于齿槽转矩的影响，相当于改变了电机的极槽配合，如果选择合适的极槽配合，则可以有效地抑制齿槽转矩。当定子齿冠开辅助槽时，假设电机的辅助槽槽口宽度与定子槽槽口宽度一样，且均匀开槽，每个定子齿上开辅助槽个数为k，若k为偶数，则:

若每个定子齿上开辅助槽数k为奇数，则:

由式(3)、式(4)可以看出，当定子齿冠上开k个槽时，由于当n为k+1的倍数时，式(3)、式(4)中Gn都不为零，且Gn的值为不开槽时候的k+1倍;而当n不为k+1的倍数时，Gn为零。故极数和槽数的最大公约数Np=1时，放大的Gn总是对齿槽转矩有影响。当Np≠1时，k的取值为k+1≠mNp时，m为整数，则被放大的Gk+1对齿槽转矩没有影响。对于本文的12槽10极外转子电机，Np=2，则k的取值为0，2，4，6等值，当k为0时，为不开辅助槽的情况。

对于外转子永磁同步电机，在定子齿冠表面开槽，涉及辅助槽的参数包括:辅助槽槽型、槽深、槽口宽度和辅助槽偏移齿冠中心线的角度。文献［8－9］给出了单一辅助槽参数与永磁同步电机的齿槽转矩之间的关系:对于辅助槽的槽型，矩形槽相较于半圆形槽和角形槽抑制齿槽转矩的效果更好，故本文选取的槽型为矩形辅助槽。对于辅助槽的槽深，随着槽深的增大，齿槽转矩幅值先下降，然后上升;对于辅助槽宽度，随着辅助槽的槽宽增加，齿槽转矩幅值亦为先下降后上升;对于辅助槽偏移齿冠中心线的角度，在辅助槽位置关于齿冠中心线对称的情况下，齿槽转矩幅值随着偏移角度的增大而先下降后上升。由以上分析可以看出，与齿冠上开辅助槽时，单一参数的变化总是对齿槽转矩抑制效果有影响，故应选取合适的参数值，以达到抑制齿槽转矩的效果最为明显。

2 电机模型建立及响应面分析

2．1 电机模型建立与齿槽转矩仿真分析

本文采用12槽10极外转子电机模型，其基本参数如表1所示。利用ANSYS Maxwell 2D建立有限元模型，模型如图1所示。

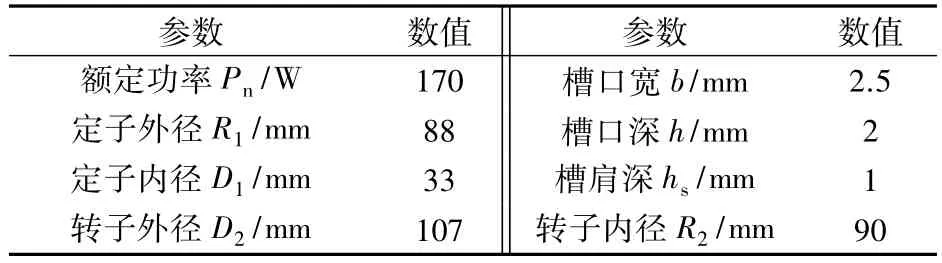
表1 电机模型基本参数

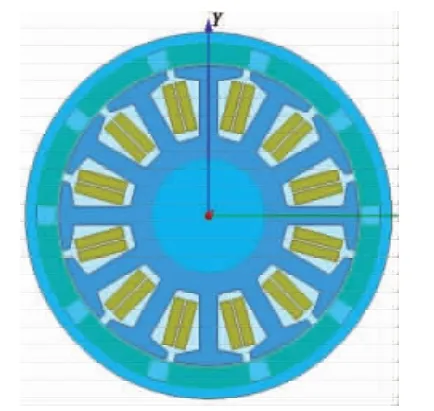
图1 优化前电机有限元模型

利用有限元软件对该模型齿槽转矩进行仿真分析，为了提高仿真精确度，采用气隙分层的方法，仿真得到的齿槽转矩波形如图2所示，可以看出齿槽转矩幅值达到41．054 2 mN·m。本文将采用开辅助槽的方法来削弱齿槽转矩，根据前面分析，12槽10极外转子电机可以开槽的最低个数为k=2，即在每个定子齿冠上开两个辅助槽，开槽方式如图3所示，其中，b代表辅助槽槽口宽，h代表辅助槽槽深，θ代表辅助槽偏移齿冠中心线角度。为了不引进新的谐波，同一个齿冠上相邻的两个辅助槽保持关于齿冠中心线对称。

图2 优化前电机齿槽转矩波形图

图3 辅助槽深度、宽度和偏移角度

2．2 响应面模型建立及回归分析

响应面法是根据合理的实验设计方法，采用不同水平下各个因素的组合方式来进行实验，并利用多维二次模型对响应以及因素之间的函数关系进行拟合，以求得最优解［11］。其中，三因素 Box－Behnken设计(以下简称BBD)将实验点安排在立方体的中点上，如图4所示，每个点代表着不同的因素组合。

图4 BBD布点示意图

本文采用的因素取值范围:槽深 h=0．1～1．1mm;槽口宽度 b=1°～4°;偏移中心线角度 θ=3°～9°。由于偏移角度过小而槽口宽过大时会造成两个相邻的辅助槽重叠，故槽口宽宜采用角度来表示，以明显区分两个辅助槽不会重叠。其中，槽口宽b=1°为 2πD1/360°=0．767 5 mm ，D1为定子外径。则不同因素的水平取值表如表2所示。采用有限元软件进行分析各种水平组合下的齿槽转矩幅值Tcogm结果如表3所示。由于在有限元软件ANSYS Maxwell 2D计算过程中采用自适应剖分，即在计算过程中不断根据计算结果进一步自动剖分，导致同样参数下的电机模型的剖分与计算结果细微的差别，所以，实验组13～17虽然因素水平一样，但是结果会有细微不同。

表2 实验因素水平表

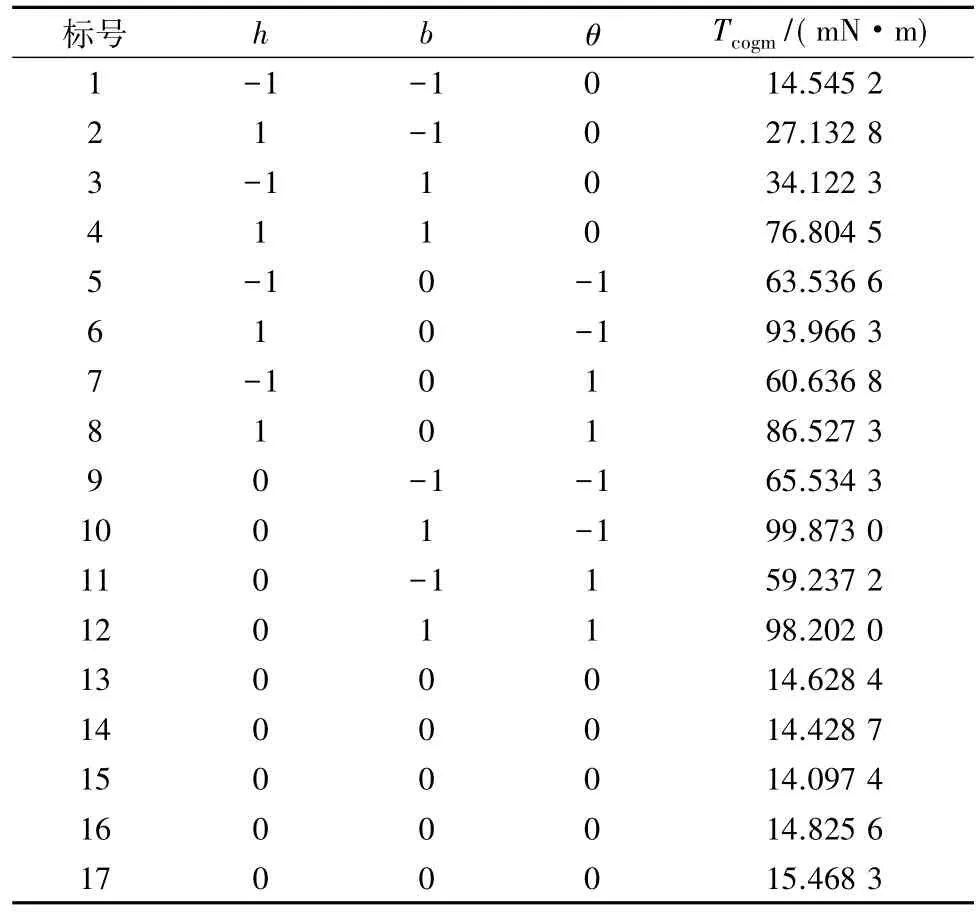
表3 BBD实验安排及有限元仿真结果

利用Design－Expert软件对仿真结果数据进行统计分析计算，采用多维二次模型对因素变量与响应之间函数关系进行拟合，拟合响应函数:

式(5)中:b，h，θ为编码变换后的数值，即其取值区间为［－1，1］。编码变换后数值与实际数值的对应关系:

式中:xi为因素实际数值，为编码变换后的数值。

为了对拟合的响应函数进行评价，采用方差分析对模型进行评价，检验模型的合理性。方差分析表如表4所示。由表4可知，模型的P检验值小于0.05，模型拟合程度较好，具有明显的统计学意义。模型失拟值的P值大于0．1，表明实验误差较小，失拟项不显著。由Design－Expert软件分析计算得到的决定系数 R2为 0．999 8，大于 0．9，说明因素变量与响应之间的关系显著，数据规律被模型较好地反映。

表4 Tcog拟合模型方差分析

2．3 响应面模型交互作用分析

为了考察各个因素之间的交互作用，利用Design－Expert绘制3D图如图5～图7所示。对于辅助槽槽宽b与槽深h两个因素，其方差分析P值小于0.001，交互作用显著。由图5可知，当偏移角度为7．5°时，相较于槽宽，随着槽深增加，响应面变化的幅度更大，说明槽深对响应值的影响更为显著。随着槽深增大，齿槽转矩幅值先下降后上升，在0．2～0．5 mm 之间取得最小值;随着槽宽增大，齿槽转矩幅值同样先下降后上升，在 1．2°～2．2°之间取得最小值。

图5 辅助槽槽宽和槽深对齿槽转矩影响

图6 辅助槽偏移角度和槽深对齿槽转矩影响

图7 辅助槽偏移角度和槽宽对齿槽转矩影响

对于偏移角度θ跟槽深h两个因素，其方差分析P 值为0．019 3，小于0．05，交互作用显著。由图6可知，当槽宽b为2．82°时，相较于槽深，随着偏移角度增加，响应面变化的幅度更大，说明偏移角度对于响应值的影响更为显著。随着偏移角度的增大，齿槽转矩幅值先是下降后上升，在5°～7°之间取得最小值。

对于偏移角度θ与槽宽b两个因素，其方差分析P 值为0．017 8，小于0．05，交互作用显著。由图7可知，当槽深h为0．6 mm时，相较于槽宽，随着偏移角度增加，响应面变化的幅度更大，说明偏移角度对于响应值的影响更为显著。综上所述，最优的辅助槽参数取值范围:槽深 h=0．2～0．5 mm;槽宽 b=1．2°～2．2°，偏移角度 θ=5°～7°。

3 PSO算法寻优及有限元软件仿真分析

为了得到最优的辅助槽参数具体数值，本文采用PSO算法对模型进行寻优，并采用式(5)响应面函数作为算法的适应度函数，最后利用有限元软件对对求取的参数数值进行仿真验算。

3．1 PSO算法寻优过程

PSO算法是一种全局算法，其目标是以最大概率依据收敛条件收敛到全局最优解［12］。

在算法运行过程中，每个粒子代表着数值解，有决定自身运动方向的位置和速度，并被适应度函数所评价。其过程根据社会认知和个体认知，即个体极值点Pbest和全局极值点Gbest进行迭代，并最终收敛于多次迭代后的全局最优极值点。粒子i在第k次的速度和位置的迭代公式如下:

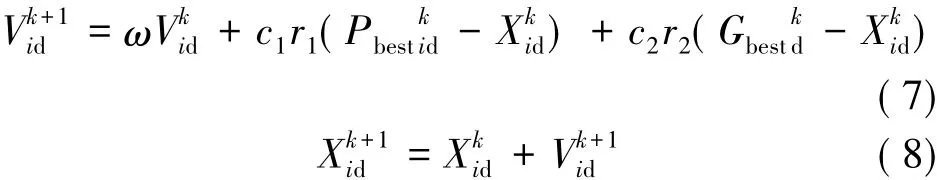
式中:ω为惯性权重;c1，c2为加速度因子;r1，r2为［0，1］之间随机数。

PSO算法流程如图8所示。设置进化代数为50 代，种群规模为 80，加速度因子 c1，c2为 1．5，利用MATLAB计算分析，结果如图9所示。可以看出，最优的齿槽转矩幅值稳定在6．510 7 mN·m，对应的辅助槽参数组合:槽深 h=0．538 8;槽宽 b=0．495 3;偏移角度θ=0．022 4。将上面参数组合按照式(6)转换为实际数值，槽深、槽宽以及偏移角度依次为0．330 6 mm，1．757 1°，6．067 1°。

图8 PSO算法流程

图9 PSO算法寻优结果

3．2 有限元软件仿真分析

利用有限元软件ANSYS－Maxwell 2D建立模型，模型参数按照寻优结果设置，辅助槽槽深度取值为 0．330 6 mm，槽宽取值为 1．757 1°，偏移角度取值为6．067 1°。仿真结果如图10所示，可以看出，齿槽转矩幅值为6．962 4 mN·m，齿槽转矩有明显的下降，与PSO算法得出的结果基本一致。

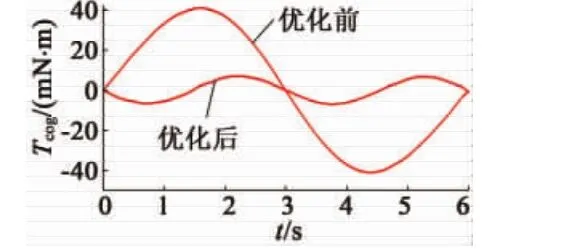
图10 优化前与优化后电机齿槽转矩对比

4 结语

为削弱一款外转子永磁同步电机的齿槽转矩，提出通过定子齿冠开辅助槽并利用RSM－PSO模型对辅助槽进行设计的方法。基于BBD对辅助槽槽深、槽宽以及偏移角度3个因素进行实验设计，通过有限元软件对电机模型进行仿真分析，采用多维二次模型对实验数据进行拟合，并通过方差分析对模型进行评价。采用PSO算法对拟合结果进行寻优，并通过有限元软件对结果分析验证，结果表明，采用本文的方法能有效抑制齿槽转矩。