基于多体系统理论的数控内外圆磨床的综合误差分析及数学模型的建立

（北京工业大学 机械工程与应用电子技术学院，北京 100124）

0 引言

随着现代制造技术的不断发展和对产品质量要求的提高，机械制造工业向高精度、高速度、高效率的方向飞速发展，精密磨削和超精密磨削加工技术已经成为行业竞争中取得成功的关键技术。数控内外磨床是大工件磨削机床和磨削中心，适用于大批量生产，宽广的加工范围让这种磨床可以作为高灵活性多功能的灵活磨床使用。作为加工孔类零件和轴类零件的主要加工工具，数控内外圆磨床的磨削质量和精度稳定性至关重要。

本文以多体系统理论[1]为基础，通过分析热误差和几何误差之间的相互耦合关系[2]，对数控内外圆磨床的几何误差和热误差[3]进行分析和研究。

1 数控内外圆磨床结构分析与误差描述

以某机床厂的数控内外圆磨床为研究对象，通过三维建模，可建立如图1所示的机床三维结构图，从图中可以得知，本机床是以加工外圆为主的数控磨床，主要有床身、头架、卡盘、Z向导轨、X向导轨以及回转砂轮架等主要部件。按照机床运动规律，可将其分为“床身-工件”运动链和“床身-刀具”运动链两个分支。如图1所示，0-1-2为“床身-工件”运动链；0-3-4-5为“床身-刀具”运动链。

其中，0为床身；1为卡盘；2为工件；3为Z向导轨；4为X向导轨；5为砂轮。

通过分析可知，对于数控内外圆磨床主要有一个旋转轴（C轴）、移动轴X和移动轴Z。空间内单个物体具有6个自由度，分别是三个位移和三个转动，因此，此机床具有9个线位移误差和9个角位移误差，另加3个垂直度误差。具体如表1所示。

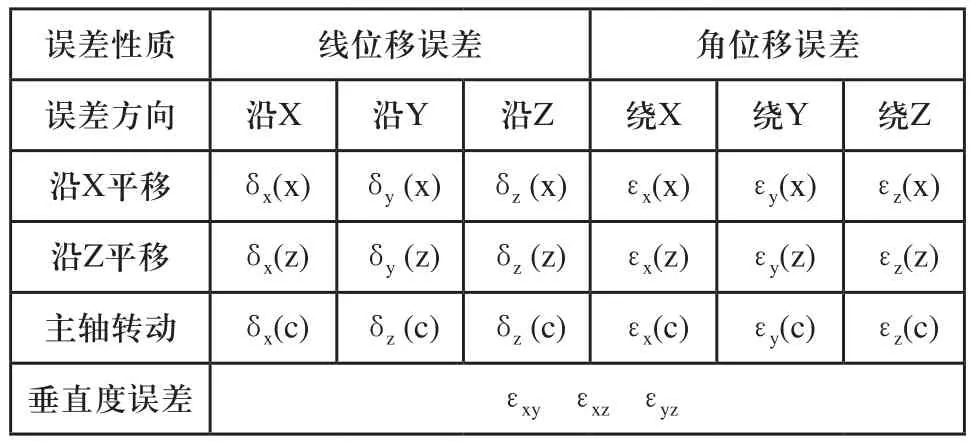
表1 数控内外圆磨床几何误差参数

在数控机床的加工过程中，几何误差和热误差是影响加工精度的主要因素。数控机床的热误差是随温度变化的函数，主要体现在X、Y、Z三个方向上的热位移。而温度对于物体的转动误差影响甚微，故此处不予考虑。通过分析可知，本机床主要存在以下热误差参数，具体如表2所示。

表2 数控内外圆磨床热误差参数

2 建立数控内外圆磨床综合误差模型

为了精确描述机床的磨削运动，需要借助各个运动部件的相对运动坐标变换矩阵，将复杂的运动转换为直观的数学模型。由图1可知，机床的两条运动链中只包含相对运动和相对转动两种运动形式[4]。通过多体系统理论构建此机床的多体系统拓扑结构图，如图2所示。图中，P为磨削点，机床通过两条运动链共同作用于点P，由此完成数控指令到运动轨迹的变换。

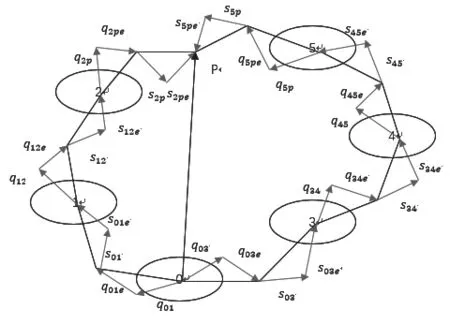
图2 数控内外圆磨床拓扑结构图

3 建立数控内外圆磨床运动学模型

此数控机床由双层工作台支撑，可根据工艺需要加工圆锥、凹槽、内外圆等结构，本文研究只针对一种加工工艺的误差分析，其他加工误差可以此推演得到。本文以加工外圆为例进行误差建模分析。

设工件坐标系为Ow-XwYwZw，刀具坐标系为Ot-XtYtZt，机床坐标系为Oo-XoYoZo，通过以上分析，P是砂轮磨削点，则点P按“床身-工件”分支在惯性体坐标系中的位置矩阵表达式为：

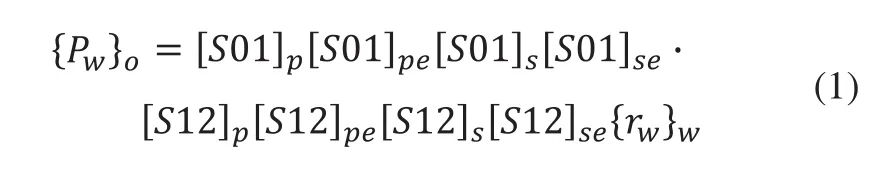
点P按“床身-刀具”分支在惯性体坐标系中的位置矩阵表达式为：

式中：{rw}w为点P在工件坐标系Ow-XwYwZw中的位置矩阵表达式，{rt}t为点P在刀具坐标系Ot-XtYtZt中的位置矩阵表达式。

在机床加工磨削过程[5]中，工件外圆轮廓是由砂轮和工件之间的相对运动复合而成，砂轮在工件上走出设计形状轨迹，必须严格控制刀具中心的实际运动轨迹总是与刀具路线重合，从而实现精密加工磨削，因此可得机床精密加工约束方程为：

4 精密加工约束方程的求解

确立了各运动部件之间的相互联系之后，进而需要明确各个部件之间的转换关系。首先，对数控机床的各个运动部件分别建立相应的子坐标系，然后确定相邻运动体变换矩阵表达式。首先确定各个坐标系的方向和位置，以机床坐标系为基准方向，床身坐标系为惯性坐标系，令Z向导轨、X向导轨和卡盘的体运动参考坐标系与其相邻的低序体的体参考坐标系重合，工件体参考坐标系和主轴参考坐标系方向一致，令床身参考坐标系绕X轴转过垂直度εyz后的方向为Z向导轨的体参考坐标系的方向，Z向导轨分别绕Z轴、Y轴转过垂直度εxy、εxz后的方向为X向导轨的体参考坐标系的方向，工件坐标系原点位于工件中心，砂轮坐标系原点位于砂轮中心，其余坐标系原点均位于主轴端面中心处。

根据数控机床相应坐标系的运动特性，建立相邻体间的变换矩阵。各几何误差变换矩阵如下：

在几何误差的基础上，需要加上热误差才能得到综合误差。热误差只考虑X、Y、Z三个方向上的位移误差，可以体现在不同的变换矩阵上[6]。

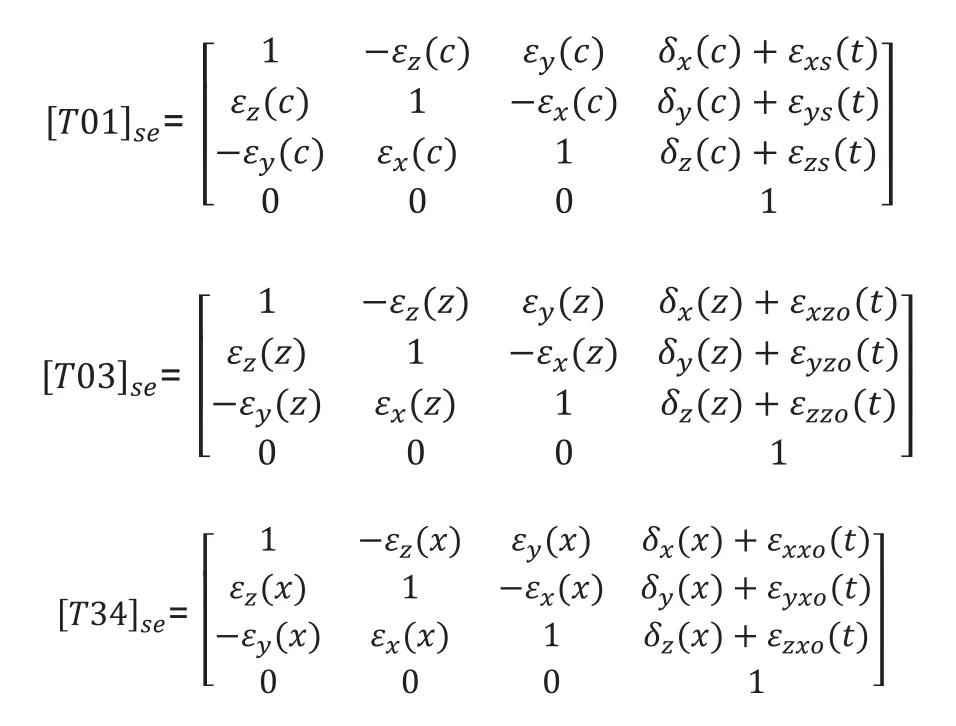
将式(1)和式(2)中的相应误差矩阵分别用以上各式进行替换，其中，[T01]se替换[S01]se，[T03]se替换[S03]se，[T34]se替换[S34]se，便可得到数控内外圆磨床的综合误差变换矩阵。通过对该机床的运动结构的分析和机床的坐标系的设定和磨削特点可知：

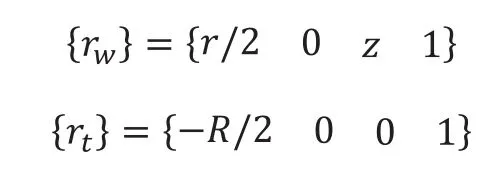
其中，r为工件截面半径 R为刀具砂轮半径。

分别将各式代入式(3)中，并略去单位矩阵，运用MATLAB求解矩阵相乘并整理消去高阶无穷小，可得如下：

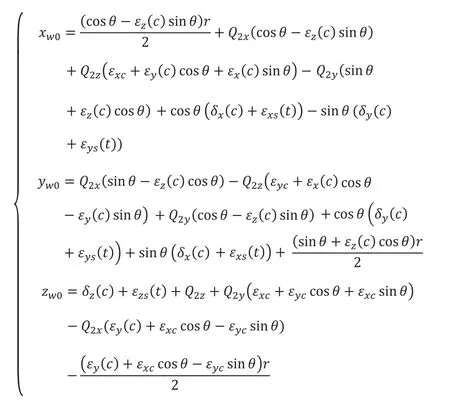
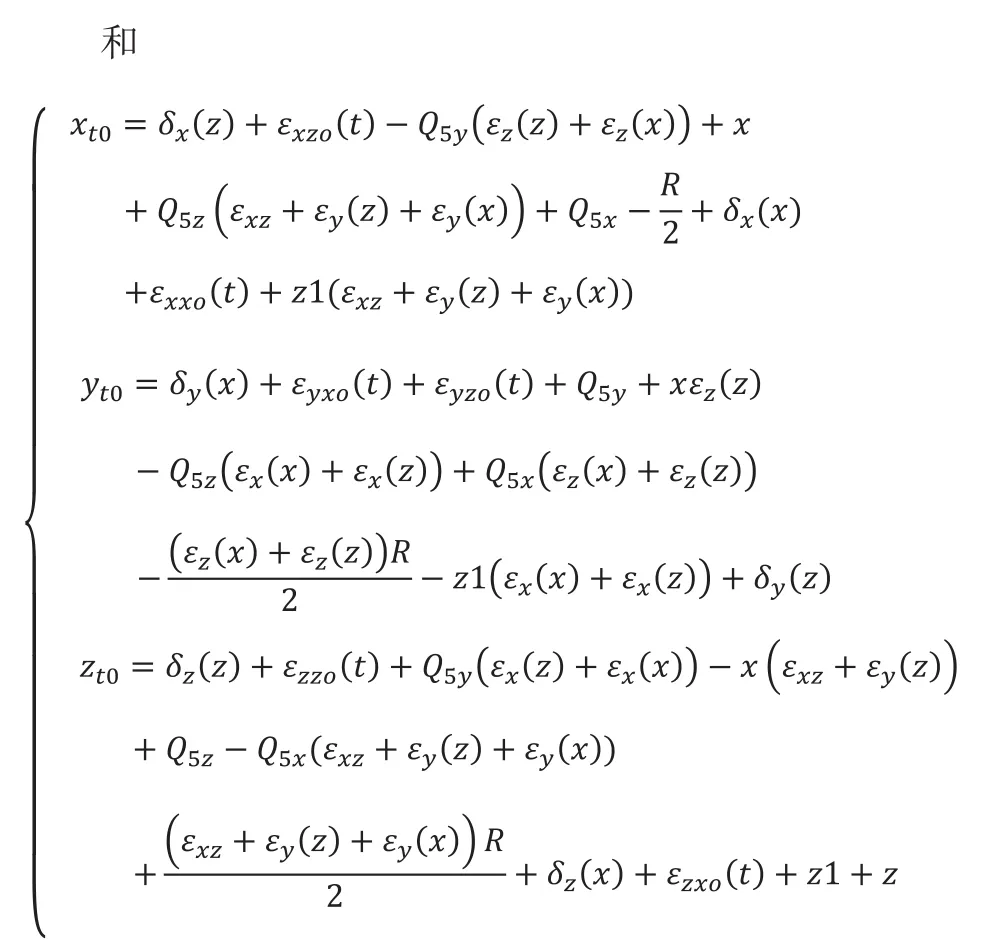
在实际加工过程中，实际刀具中心点应与工件坐标系上的理论刀具中心点在任意时刻重合，这是实现精密加工的必要条件，将上述计算结果带入公式中，即：

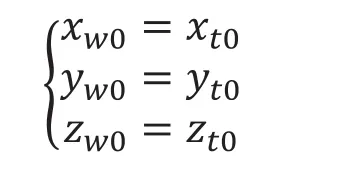
便可求出该数控磨床的精密加工约束方程。在已知精密加工约束方程的情况下，只需对其相关参数进行测量和辨识，包括几何误差和热误差两部分。然后误差参数代入建立的刀具路线和数控指令以及数控指令和实际刀具轨迹之间的映射关系来修正数控指令以达到误差补偿的目的。

5 结论

1）通过对数控内外圆复合磨床进行三维建模，对其进行结构分析，利用多体系统理论对机床结构进行描述，将机床分为两个分支、多个部件，确立每个运动部件的体参考坐标系。

2）通过分析数控磨床运动结构，得出该机床共有21项几何误差和9项热误差（忽略热误差对转角的影响）。

3）在多体系统理论的基础上，推导出该机床各个运动部件间的相对运动坐标变换矩阵，通过分析热误差特性，揭示了热误差和几何误差之间的耦合关系，进一步建立该机床的综合误差数学模型，为后续的误差补偿奠定了基础。