非均匀收敛随机介质模型对浅埋隧道施工引起地表沉降预测研究

王 翀,秦拥军,于广明,高丽燕

(1.新疆大学建筑工程学院,乌鲁木齐 830047； 2.青岛理工大学土木工程学院,青岛 266033)

非均匀收敛随机介质模型对浅埋隧道施工引起地表沉降预测研究

王 翀1,秦拥军1,于广明2,高丽燕2

(1.新疆大学建筑工程学院,乌鲁木齐 830047； 2.青岛理工大学土木工程学院,青岛 266033)

针对软弱土层中的浅埋大跨隧道在施工过程中出现的初支变形、断面底部隆起等现象,通过对原有的断面收敛模式进行修正,提出考虑初支变形与断面底部收敛的统一收敛模式,并以单洞及双洞椭圆隧道为例,推导出该种收敛模式下隧道施工中产生地表沉降的随机介质法预测公式,应用遗传-蚁群混合算法(GA-ACA)解决该预测模型的参数反演计算问题。为验证该模型对浅埋隧道地表变形预测的准确性,以乌鲁木齐地铁1号线三—新区间某典型断面为例,分别使用均匀收敛、底部为0、底部非0以及统一收敛模式等4种收敛模式进行参数反演,并将反演结果与现场监测结果做对比,研究结果表明：统一收敛模式与隧道断面实际变形规律更加吻合,其预测精度要比不考虑初支变形与断面底部收敛时的预测精度更高,即对浅埋、超浅埋隧道而言,初支变形以及底部隆起等现象对地表变形预测结果产生的影响不可忽略。

隧道工程；地表变形；随机介质理论；非均匀收敛；底部隆起；初支变形

随机介质理论最早由波兰学者J.Litwinszyn提出，后经我国学者刘宝琛、阳军生等[1-2]发展应用于地铁隧道施工引发的沉降预测中。刘宝琛等人在考虑隧道产生的地层损失时，假定断面的收敛是均匀的。然而在实际工程中，由于受地层的初始应力、土体的软硬不均以及施工工艺等多种因素影响，其收敛形式并非是均匀的。Loganathan、Lee等[3-4]提出了开挖断面底部土体收敛值为0的非均匀收敛模式，其计算结果表明相较于常用的均匀收敛模式而言，该假定与实际情况更加符合。韩煊[5]将上述非均匀收敛模式首次引入随机介质理论中，并经算例分析验证了该模型计算结果的准确性。伍振志[6]针对隧道开挖后底部土体隆起的情况，通过分别假定断面上下边缘的收敛值的方法来考虑底部隆起的影响，并取得了较好的效果。

在随机介质理论中，隧道断面任何位置出现的地层损失，都会引起地表沉降，并且地表沉降槽的深浅、形状与地层损失的大小以及位置等有着直接关系。对于深埋隧道而言，开挖断面自身的收敛模式对土层变形的计算结果(尤其是地表沉降)影响不大。但是对于埋深较浅的隧道来说，不同的断面收敛模式还是会对计算结果造成明显的影响。尤其是对于软弱土层中的浅埋、超浅埋隧道，隧道施工中断面底部的隆起、初支变形等现象对地表移动变形影响更加不能忽略[7-8]，显然，上述学者提出的开挖断面收敛模式在浅埋、超浅埋隧道的适用性值得探讨。

在总结前人研究的基础上，考虑底部隆起以及初支变形的影响，修正并提出一种适应于浅埋大断面的统一收敛模式，推导单洞及平行双洞椭圆隧道在该模式下的随机介质预测模型计算公式，并以乌市地铁1号线某标段实测数据为基础，使用遗传—蚁群混合算法(GA-ACA)对相应参数进行反演，以证明该收敛模式在浅埋大断面隧道地表变形预测中的优越性。

1 随机介质理论与方法

随机介质理论以概率论为基础，假定地层岩土体为随机的介质，从而可以用叠加方法来计算岩土体位移。假定地表以下Z=η深度任一点(ξ，η)处的微元dξdη开挖并完全坍塌(图1)，则对地表产生的影响为[1]

对于一个埋深为H的隧道，通过一定的收敛边界可以计算出隧道开挖导致的地表沉降值。假定隧道开挖前断面面积为Ω，收缩后断面面积为ω，则整个断面收敛部分面积为Ω-ω，则隧道开挖引起的地表沉降值S(X)可以视为区域Ω-ω全部传递到地表并引起的沉降，即

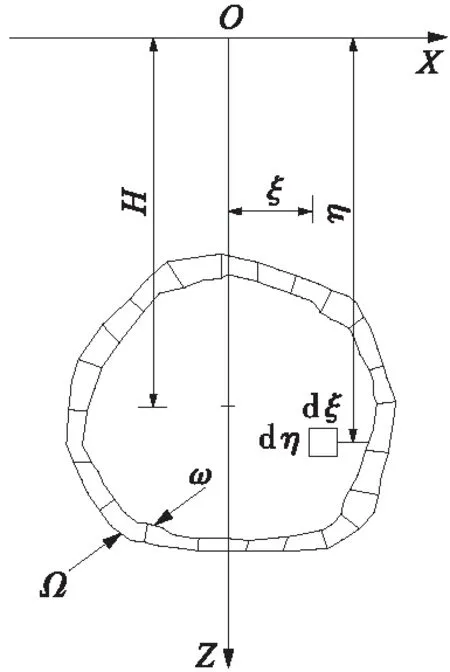
图1 单元及断面开挖示意

其中,β为地层影响角。

对式(2)求导可得出地表倾斜T(X)与地表沉降曲线曲率K(X)的表达式

对式(2)～式(4)进行积分即可得到隧道开挖产生的地表沉降、倾斜度及曲率等变形值。由于上式的被积函数不可积，因此可以使用Legendre-Gauss数值积分法，通过Matlab软件，编写程序进行计算。

2 隧道开挖断面收敛模式的修正

由上文可知，要想对某一隧道上方地表沉降值进行准确预测，必须要确定两个关键的变量：收敛边界Ω-ω与影响角β。而大多数情况下影响角β值的确定，又是通过对地表实测位移依据假定的收敛模式进行反演而得到的，因此隧道开挖沉降预测的准确性取决于断面收敛模式的准确性。

如图2所示，以上几种断面收敛模式均认为断面收敛前后形状相同，即仅考虑断面收敛半径及收敛后断面形心的变化，未考虑初支变形的情况。

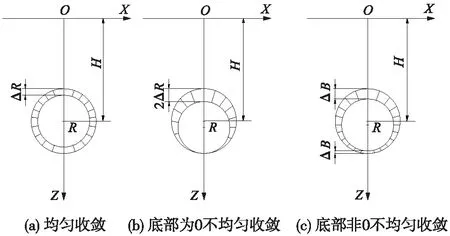
图2 隧道断面不同收敛形式

C Gonzalez，C Sagaseta等[9]人的研究表明，隧道开挖后断面底部土体由于应力释放不但会产生一定程度的隆起现象，且隧道初期支护在上部围岩压力与底部土体的相互作用下会发生椭圆化变形。因此，隧道断面实际的变形过程可以简化为以下3步，如图3所示。

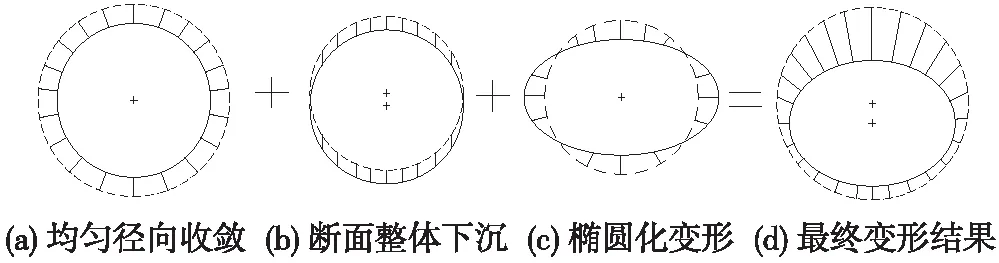
图3 隧道开挖收敛模式示意

然而，必须指出的是，在实际工程中，由于受地层的初始应力、土体的软硬不均以及施工工艺等多种因素影响，隧道断面实际的收敛形式也不尽相同。图3所示的隧道收敛模式也仅仅是理想条件下的假定，并不能完全真实地反映出实际的收敛情况。但与图3所示的几种传统收敛模式相比，该假定无疑更为合理。

3 基于统一收敛模式预测模型的建立

为了使隧道的收敛形式更加接近真实情况、更具有代表性，本文对原有收敛模式进行修正并提出考虑初支椭圆化变形与底部隆起的统一非均匀收敛模式。在该模式中认为，隧道开挖后首先发生断面径向收敛(收敛值为ΔR)，然后整个断面整体下移(断面形心的竖向位移为ΔH，其中0≤ΔH≤ΔR)，最后由于隧道初期支护的受力变形隧道发生椭圆化变形(变形前后面积不变)，如图3所示。

为定量的描述初支断面椭圆化的程度，引入一个新的参数：椭圆化系数α，令

式中,A0为隧道初支变形前断面跨度；A1为隧道初支变形后断面跨度。

在上述假定的基础上，为了更具代表性，以椭圆断面为例(圆可视为椭圆特例)，推导出该模式下的单洞和平行双洞隧道在式(2)～式(4)式中的8个的积分界限，如表1、表2所示(其中：参数a、b、c、d为隧道开挖前原有断面区域积分上下限；e、f、g、h为隧道开挖收敛后的断面区域积分上下限)。

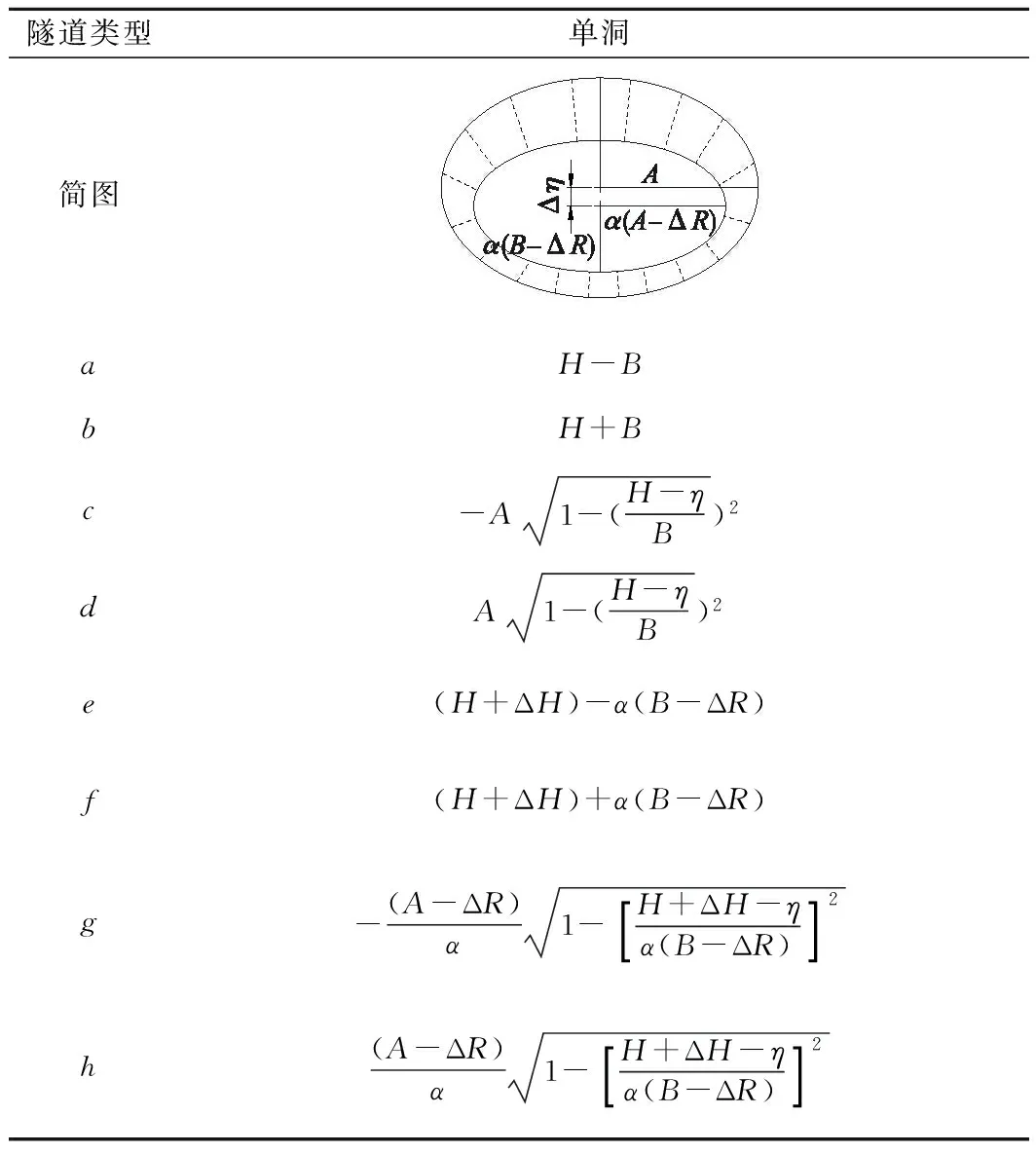
表1 单洞隧道统一收敛模型积分界限

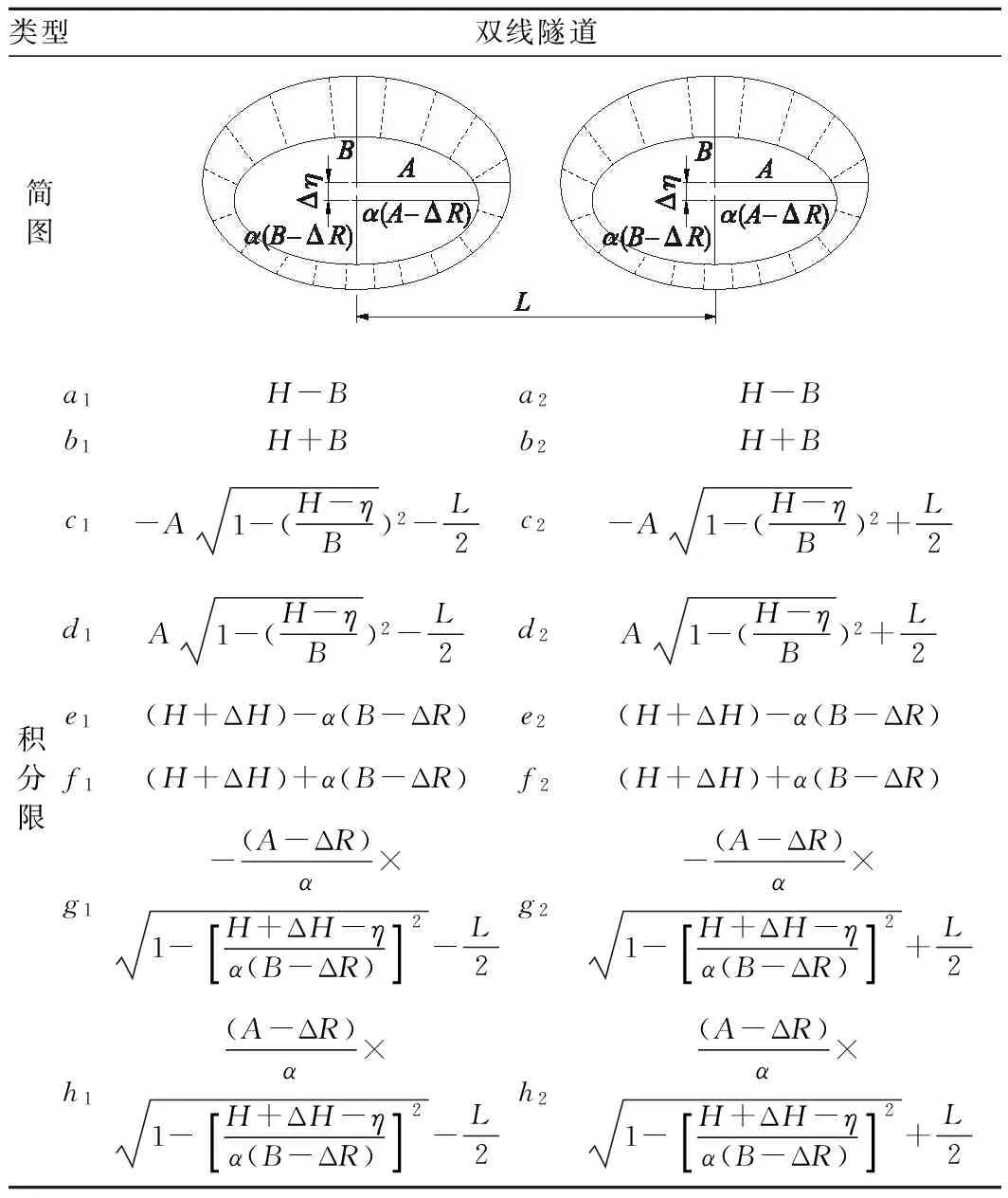
表2 双洞隧道统一收敛模型积分界限

4 基于GA-ACA模型参数反演

基于该种收敛模式的随机介质预测模型进行预测时，需要4个基本参数：ΔR、ΔH、α和tanβ(β为影响角)。为确定预测所需的相关参数，一般以现场实测地表位移为基础，进行参数反演得到。为此，定义目标函数F(x)为

式中m——地表沉降测点数；

Si——理论计算值；

x={ΔR，ΔH，tanβ，α}。

同时式(6)还需符合下列约束条件

参数反演的目的在于寻得一组参数x={ΔR，ΔH，tanβ，α}，在满足约束条件的前提下，使目标函数F(x)达到极小值，实际上可以转化为数学中优化计算问题。由于上述预测模型的参数反演属于复杂的非线性优化问题，普通的优化算法在优化此类问题时易出现收敛过早、陷入局部极值等现象。蚁群算法与遗传算法相结合形成混合算法(GA-ACA)[10],其结合了两种算法的优点，不但拥有遗传算法的随机、全局收敛等特点，还兼顾了蚁群算法求精效率高等优点，在计算复杂的多参非线性优化问题时，展现出极佳的适应性。

4.1 GA-ACA算法描述

GA-ACA算法在进行优化计算时，首先利用遗传算法对目标问题的初始信息要素进行全局搜索；然后在求出初始信息要素分布的前提下，利用蚁群算法求精解、效率高等特点来求解。具体步骤如图4所示。

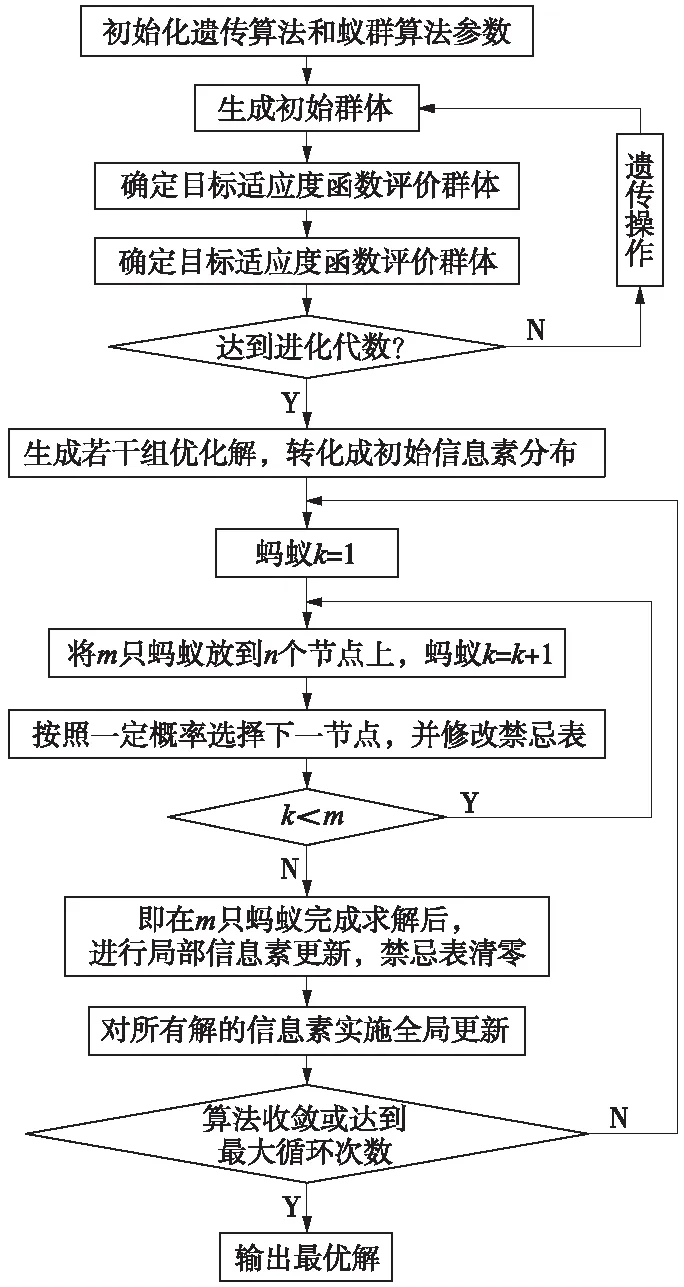
图4 GA-ACA算法流程

4.2 GA-ACA算法要素的确定

(1)解空间的确定。为避免遗漏最优解，应将参数的空间范围尽可能取大，所以取β∈[10°，80°]，ΔR∈[0，R/2]，ΔH≤ΔR，其中R为隧道开挖半径。

(2)适应度函数的构建。为将上述参数反演模型中求目标函数最小值的问题变换为遗传算法求适应度函数最大值的问题，需构建相应的适应度函数

其中,x={ΔR，ΔH，tanβ，α};F(x)为式(6)中的目标函数。

(3)各种参数的选择。目前遗传算法与蚁群算法的参数大都是根据经验确定，根据已有的计算经验，结合相关文献[11-13]取的参数如下：遗传算法基本参数，种群规模n=100，最大进化代数T=200，交叉概率Pc=1.0，变异概率Pm=0.01；蚁群算法参数，蚁群规模N=20，信息素控制参数α=0.8，能见度控制参数γ=0.9，常数Q=10，信息素的保留系数ρ=0.6。

依据遗传-蚁群算法原理及上文推导的地表变形预测公式，采用Matlab编制相应参数反演程序，以隧道开挖过程中的地表沉降实测值为基础，可对该收敛模式下的预测参数进行反演。

5 算例分析

乌市地铁1号线三屯碑站—新疆大学站区间全长738.412 m，覆土厚度5～15 m，由南向北逐渐加深。其中小线间距段暗挖区间为单洞双线隧道，长224.751 m，隧道开挖断面宽12.78 m，高9.2 m。表3所示为三新区间小线间距段暗挖隧道某断面地表沉降实测值(该断面埋深约8.1 m，相对埋深0.986)。

表3 某典型断面地表沉降实测值

注：S—地表各测点沉降实测值；X—测点与隧道轴线的水平距离。

为验证上述统一收敛模型在浅埋大断面隧道开挖变形预测中的科学性和合理性，采用编写的参数反演程序对均匀收敛、底部为0收敛模式、底部非0收敛模式、统一收敛模式下的预测参数进行反分析，其结果如表4所示，不同收敛模式下的预测沉降槽曲线与沉降实测值如图5所示。

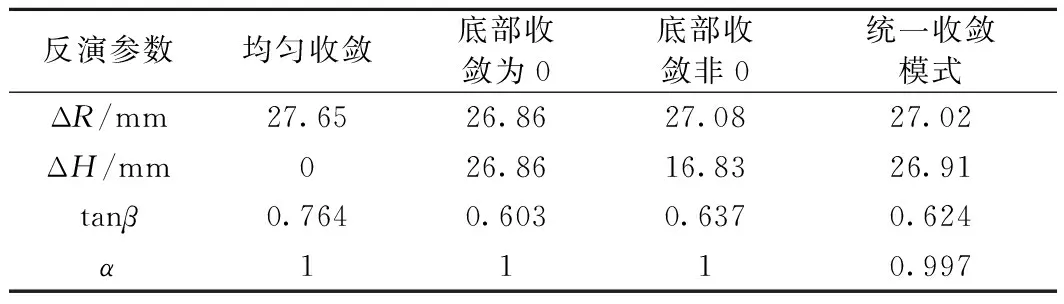
表4 不同收敛模式下的反演参数值

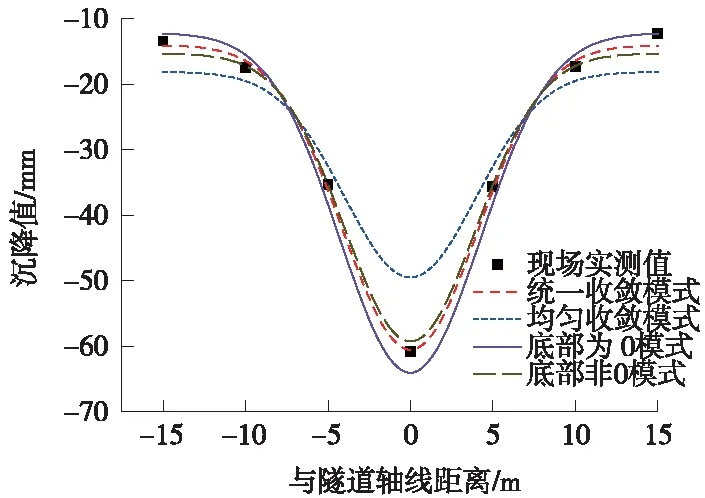
图5 不同收敛模式下地表沉降预测曲线与实测值

韩煊等研究表明[5-7]，不同隧道断面收敛形式对地表变形预测结果的差异，与隧道的埋深有着直接关系，且隧道埋深越浅，计算结果之间的差异就越明显。而当隧道的相对埋深小于1.3时(即：H0/A<1.3时)，不同收敛形式之间的最大差异可达20%左右。

由图5可知，对于浅埋隧道而言(该断面相对埋深0.986)，考虑底部隆起的统一收敛模式预测精度要明显高于均匀收敛模式及底部为0收敛模式，与考虑底部土体隆起的底部非0收敛模式相比也与真实值更加吻合。其中在靠近隧道中心轴线处4种收敛模式的差异最大，各收敛模式下预测值与实测值的最大差值分别为：0.95 mm，-1.64 mm，4.26 mm，-13.58 mm。

为进一步定量分析上述不同收敛模式下预测模型的精度，采用灰关联度分析法对不同模型的预测值进行分析，其具体的计算步骤如下[14]。

设置参考序列：x0={x0(k)}(k=1，2，…，m)；比较序列：xi={xi(k)}(k=1，2，…，m；i=1，2，3)，其中m为地表沉降测点数。定义关联系数λ0i(k)与关联度r0i如下

式中，ρ为分辨系数；ρ∈(0，1)，取ρ=0.5。

定义关联度

分析结果表明：统一收敛模式、底部非0收敛模式、底部为0收敛模式和均匀收敛模式等4种收敛模式下沉降预测曲线的非关联度分别为0.893，0.857，0.786和0.634，即考虑底部隆起和初支变形的统一收敛模式预测精度更高，同时也表明在浅埋大断面隧道的地表变形预测中，底部隆起等现象对地表变形预测结果产生的影响不可忽略。

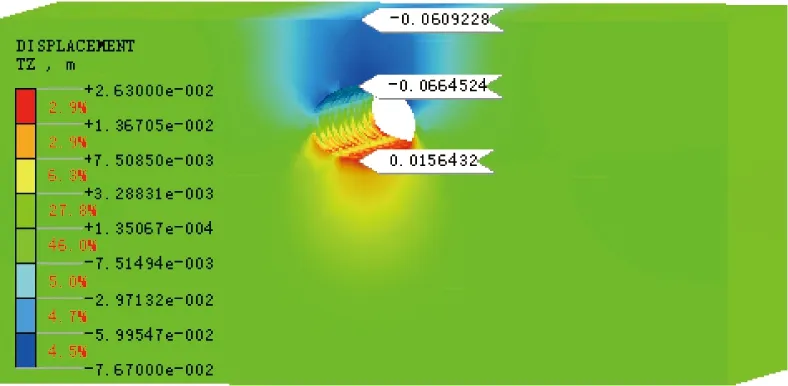
图6 开挖断面竖向位移云图

同时，由开挖断面的竖向位移场云图(图6)可知，隧道拱顶的下沉值约为66 mm，隧道仰拱部位出现了约15 mm的隆起，这与本文统一收敛模式的反演值较吻合。由此可见：考虑底部隆起和初支变形的统一收敛模式与隧道断面的实际收敛情况更加吻合。其中：各收敛模式下开挖断面关键位置反演值与模拟结果对比如表5所示。

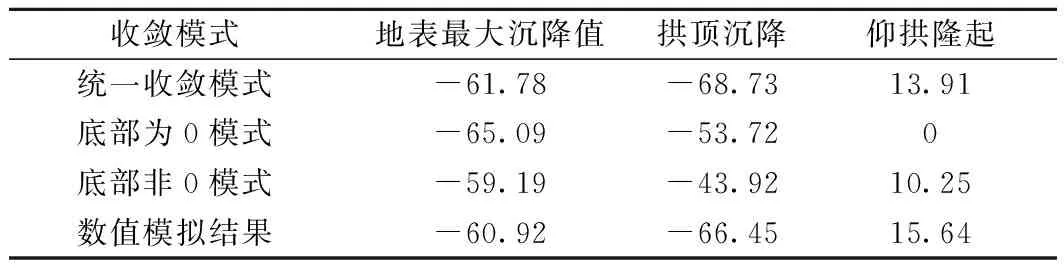
表5 各收敛模式下开挖断面关键位置反演值与模拟结果对比 mm

6 结论

(1)为充分考虑隧道开挖产生的初支变形和底部土体隆起等现象的影响，引入断面收敛前后形心竖向位移ΔH以及初支椭圆化变形系数α两个新的参数，建立了考虑底部土体隆起的统一收敛模型，并推导出该统一收敛模式下，单洞及平行双洞椭圆隧道的随机介质法公式，使随机介质法更加合理，适用性更强。

(2)针对该统一收敛模式下随机介质预测模型参数求解工程中的多参反演问题，采用遗传—蚁群算法(GA-ACA)对该模型的参数进行优化计算，经实例计算表明，该种算法具有优秀的收敛性及稳定性。

(3)经实例验证表明，统一收敛模式与隧道断面实际变形规律更加吻合，其预测精度比传统的收敛模式下的预测精度更高。即对浅埋、超浅埋隧道而言，施工中产生的初支变形以及底部隆起等现象对地表变形预测结果产生的影响不可忽略。

[1] 刘宝琛，张家生.近地表开挖引起的地表沉降的随机介质方法[J].岩石力学与工程学报，1995，14(4)：289-296.

[2] 阳军生，刘宝琛.城市隧道施工引起的地表移动及变形[M].北京：中国铁道出版社，2002：15-25.

[3] Loganathan N，Poulos H G. Analytical prediction for tunneling-induced ground movements in clays[J]. Journal of Geotechnical and Geo-environmental Engineering，1998，124(9)：846-856.

[4] Lee K M， Rowe R K， Lo K Y. Subsidence owing to tunneling Iestimating the gap parameter[J]. Canadian Geotechnical Journal， 1992，29(6):929-940.

[5] 韩煊，李宁.隧道开挖不均匀收敛引起地层位移的预测模型[J].岩土工程学报，2007，29(3)：347-352.

[6] 伍振志.基于非均匀收敛模式的隧道地表变形的随机介质预测模型[J].中南大学学报(自然科学版)，2010，41(5)：2005-2010.

[7] 韩煊.隧道施工引起的地层位移及建筑物变形预测的实用方法研究[D].西安：西安理工大学，2006.

[8] 张海波，殷宗泽，朱俊高.地铁隧道盾构法施工过程中地层变位的三维有限元模拟[J].岩石力学与工程学报，2005，24(5):755-760.

[9] Gonzalez C， SagaSe C. Patterns of soil deformation around tunnels. Application to the extensin of Madrid Meteo. Computers& Geotec-hnics，2001，28:445-468.

[10] 武交峰.应用遗传算法提高蚁群算法性能的研究[D].太原：太原理工大学，2007.

[11] 李守巨，刘迎曦，孙伟.智能计算与参数反演[M].北京：科学出版社，2008.

[12] 查剑锋，冯文凯，朱晓峻.基于遗传算法的概率积分法预计参数反演[J].采矿与安全工程学报，2011，28(4)：655-659.

[13] 贾新果.基于蚁群算法的开采沉陷计算参数反演[J].工矿自动化，2015，41(6):10-13.

[14] 刘思峰，党耀国，方志耕，等.灰色系统理论及其应用[M].北京：科学出版社，2010.

Study on Prediction of Ground Surface Settlement Caused by Construction of Shallow Buried Tunnel based on Non-uniform Random Medium Model

WANG Chong1, QIN Yong-jun1, YU Guang-ming2, GAO Li-yan2

(1. College of Architecture Engineering, Xinjiang University, Urumqi 830046, China; 2. Civil Engineering College, Qingdao Technological University, Qingdao 266033, China)

Aiming at the phenomenon of the initial support deformation and the uplift in the bottom of the shallow buried large-span tunnel in soft soil, a unified convergence model considering initial support deformation and the bottom of the cross section is proposed based on the modification of the original section convergence model. With reference to single-hole tunnel and double-hole elliptical tunnel, the formula for ground settlement prediction in stochastic medium method is derived based on the convergence mode in the tunnel construction, and the genetic and colony algorithm (GA-ACA) are used to solve the problem of parameter inversion in the prediction model. In order to verify the accuracy of the model, this paper refers to Urumqi Metro Line 1 in SAN-XIN district and uses 4 kinds of different convergence mode parameter inversions such as uniform convergence, the bottom 0, the bottom not 0 and a unified convergence mode. The inversion results and the measured values are compared, and the results show that the uniform convergence model is more consistent with the actual deformation law of tunnel section, and the prediction accuracy is higher than that without considering the deformation of the primary support and the convergence of the bottom section. As far as the shallow buried tunnel and ultra shallow buried tunnel are concerned, the effects of the initial deformation and the bottom heave on the surface deformation prediction should not be ignored.

Tunnel engineering; Surface deformation; Stochastic medium theory; Non-uniform convergence; Bottom heave; Initial deformation

1004-2954(2018)01-0104-05

2017-03-06；

2017-04-17

国家自然科学基金资助项目(51374135)

王 翀(1990—)，男，2017年毕业于新疆大学，工程硕士，E-mail：923707616@qq.com。

U457

A

10.13238/j.issn.1004-2954.201703060002