基于应变能密度的P92钢蠕变-疲劳寿命可靠性模型研究

纪冬梅, 郭恒超, 任建兴, 孙 权, 戴 晨， 朱全军

(1. 上海电力学院 能源与机械工程学院， 上海 200090； 2. 全球能源互联网研究院， 北京 102211)

P92钢作为主蒸汽管道用钢时，在服役过程中其微观组织和沉淀强化相逐步发展演化，马氏体条带宽度增加，位错密度减小，并逐步出现M23C6碳化物和MX碳氮化物的聚集、粗化及析出Laves相[1-2]。M23C6中W含量降低，且消耗了基体的W和Mo，造成固溶强化作用下降；Laves相的粗化速度较快，随着时效时间的延长，颗粒会出现明显的聚集和粗化，当长大到一定尺寸时容易诱发形成蠕变孔洞[3]。机组参与调峰运行时，启停频繁，负荷变化幅度大，主蒸汽管道承受剧烈的温度变化和交变热应力，从而产生严重的低周疲劳损伤。

材料局部产生的疲劳裂纹为疲劳损伤，是一种由表及里的断裂过程，材料内部形成晶界孔洞则是蠕变损伤。研究表明，在高温、介质环境条件下，当穿晶疲劳裂纹与晶界孔洞相遇时，金属材料内部存在蠕变-疲劳交互作用[4-8]，即疲劳裂纹与蠕变孔洞相互促进、相互发展[9]或相互抑制[10-11]，形成交互作用。就火电机组高温部件的工作条件而言，随着工作温度不断提高，这2种损伤的交互作用越来越明显；氧化现象对蠕变损伤和疲劳损伤存在促进与钝化作用的竞争与耦合[12]。

蠕变-疲劳交互作用的存在给蠕变-疲劳寿命预测带来一定的难度。目前，代表性的蠕变-疲劳寿命预测方法主要有线性累积损伤法[13]、延性耗损模型[14-15]、应变范围和应变能划分法[16]、连续损伤力学模型等[17]，这些模型均具有特定的应用条件，需确定较多的材料常数或进行大量试验等，出现工程适用性不佳等问题。此外，关于在应力控制下适合蠕变-疲劳寿命预测的方法未达成共识，因此采用应力加载模式进行材料蠕变-疲劳交互作用的试验研究在工程应用上具有重要意义。

基于此，笔者在600 ℃下对P92钢进行了应力控制的蠕变-疲劳试验，并基于适用于应力控制的蠕变-疲劳寿命预测模型，将实际工况下的应力和应变能密度作为随机变量，分析了P92钢在不同工况下蠕变-疲劳寿命的可靠度和不同可靠度下的蠕变-疲劳寿命。

1 基于应变能密度的蠕变-疲劳寿命可靠性模型

在不同荷载作用下，构件的失效过程实质是一个复杂的能量转化耗散过程。外荷载对构件所做的功使构件产生不同性质的宏观变形，即外加的机械功转化为相应的应变能，其中只有造成塑性变形和蠕变变形等不可恢复的非弹性应变能，才能对构件造成损伤，这些损伤在外力不断作用下累积，最终导致构件失效断裂。因此，在一定程度上外荷载所做的功转化成引起材料损伤的应变能，从而导致构件失效。研究发现，拉伸荷载与压缩荷载均会对材料造成损伤，降低材料的疲劳寿命。与拉伸状态相比，压缩保载作用下的疲劳寿命减幅更为明显[7, 18-19]。

1.1 基于应变能密度的蠕变-疲劳寿命预测模型

(b) σtmin<0图1 应力控制的蠕变-疲劳试验的应力-应变曲线Fig.1 Stress-strain curves obtained by load-controlled creep-fatigue tests

(1)

式中：Δup为每一循环的应变能密度；εt为真实应变；σt为真实应力。

利用函数在坐标轴上的积分进一步计算σtmin≥0和σtmin<0时的应变能密度，详见文献[20] 。

(2)

应变能密度与蠕变-疲劳寿命的关系可表示为：

(3)

式中：Nf为蠕变-疲劳的荷载循环次数，即疲劳寿命；A和m均为材料参数，与材料和温度有关。

1.2 P-Δup-Nf曲线

在蠕变-疲劳试验过程中，耐热钢每一循环的应变能密度呈三阶段特征，即急剧减小、稳定和快速增加[20]。在稳定阶段，应变能密度Δup变化较小，但在实际服役过程中，即使负荷相同，高温承压部件所受荷载为随机荷载，承压部件的寿命也是随机变量，服从某一分布。

对式(3)两边求对数，可得：

lgNf=lgA-mlg Δup

(4)

由于材料承载能力和服役环境的随机性，应变能密度与寿命之间存在一定的不确定性。根据实际服役条件，其应变能密度分别为Δup1、Δup2、…、Δupn，相应的疲劳寿命分别为Nf1、Nf2、…、Nfn。假设材料参数lgA和m服从正态分布或Gaussian分布，式(4)中lgA和m为随机变量lgA和m的中值，可由试验数据拟合得到。

对于随机变量m，其方差为：

(5)

式中：sm为材料参数m的标准差；slg Nf为对数寿命lgNf的标准差。

(6)

在不同可靠度下lgA为：

(7)

式中：μP为可靠度P对应的标准正态分布函数。P=50%时，μP=0；P=97.72%时,μP=-2；P=99.87%时，μP=-3。

将式(7)代入式(4)，得到不同可靠度下的蠕变-疲劳寿命。

图2 lg A的概率密度函数示意图Fig.2 Sketch of probability density function of lg A

(8)

由式(8)可以得到不同可靠度下应变能密度与蠕变-疲劳寿命之间的关系曲线，即Δup-Nf曲线，将式(8)定义为P-Δup-Nf曲线。

1.3 基于P-Δup-Nf曲线的蠕变-疲劳寿命可靠性模型

1.3.1 蠕变-疲劳寿命的概率分布函数

根据定义的P-Δup-Nf曲线，可计算出在确定应变能密度Δup下不同可靠度对应的蠕变-疲劳寿命Nf，从而通过统计的方法获得其服从的分布。由于承压部件的应变能密度Δup不可能是确定值，所以采用式(8)计算Nf时，应把Δup作为随机变量；又因为Nf服从的分布与Δup有关，所以计算lgNf时不需把Δup作为具体数值，而是直接用lg Δup来表示lgNf。一般情况下，认为寿命服从对数正态分布，可根据一组lgNi进行估计。

(9)

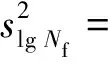
(10)

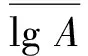
(11)

1.3.2 疲劳寿命的可靠度模型

基于P-Δup-Nf曲线，考虑应变能密度的不确定性影响，推导出疲劳寿命可靠度的计算模型。

图3以双对数坐标给出了P-Δup-Nf曲线和疲劳寿命的概率密度函数。其中：Na为某一Δup下失效寿命的中值；N0表示极限疲劳寿命；f(Δup)表示应变能密度Δup的概率密度函数；f(Nf|Δupi)表示某一确定机械功密度下疲劳寿命的概率密度函数；阴影面积表示寿命为Ni时的可靠度。

图3 P-Δup-Nf曲线与Nf的概率分布函数Fig.3 Curve and probability density function of Nf

当应变能密度在Δupi～(Δupi+dΔup)内取值时，Nf>Na的概率为：

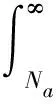
(12)

应变能密度Δup落入Δupi～(Δupi+dΔup)区间的概率为：

P(Δupi≤Δup≤(Δupi+dΔup))=g(Δup)dΔup

(13)

应变能密度Δup落入Δupi～(Δupi+dΔup)区间与寿命(Nf>Na|Δup)是2个相互独立的事件，同时发生的概率为：

P(Δupi≤Δup≤(Δupi+dΔup))P(N>Na|Δupi)=

(14)

由于Δup是任意取定的，将Δup所有可能取值的概率加起来，即为所求的可靠度。

R(Na)=P(Nf>Na|Δup)=

(15)

当应变能密度Δup服从的分布已知，可根据式(15)计算疲劳寿命的可靠度。反之，已知在某工况下承压部件应变能密度Δup所服从的分布及其期望疲劳寿命的可靠度，可由式(15)计算出承压部件期望可靠度下的疲劳寿命。

2 P92钢的蠕变-疲劳试验

2.1 试验材料

P92钢管产自Wyman-Gorden公司，其内径为914 mm、壁厚为50 mm，热处理工艺为正火1 065 ℃/1.25 h，风冷，回火776.7 ℃/2.5 h，空冷，金相组织为回火马氏体结构，晶粒度为7.5级。材料的化学成分见表1。

表1 P92钢的化学成分Tab.1 Chemical composition of P92 steel %

2.2 蠕变-疲劳交互试验与试样

根据GB/T 2039—1997 《金属拉伸蠕变及持久试验方法》，进行蠕变-疲劳交互试验时采用圆形横截面标准蠕变试样，其直径D0=10 mm，原始计算长度L0=100 mm，详细尺寸见图4(a)。在GWT-2504电子高温蠕变持久试验机上进行高温蠕变-疲劳交互试验，加载波形为梯形波，利用应力控制加载，加载速率为3 MPa/s，如图4(b)所示，其中Tht为荷载高位保载时间，Thc为荷载低位保载时间。试验过程中指示温度与指定的试验温度相差不能超过±3 K，温度梯度不超过3 K，采用引伸计测量轴向变形。

(a) 圆形横截面试样(b) 加载波形

图4 蠕变-疲劳试验的圆形横截面试样及其加载波形

Fig.4 Loading wave for creep-fatigue tests with cylindrical specimens

2.3 蠕变-疲劳交互试验结果

表2给出了P92钢在600 ℃不同试验条件下蠕变-疲劳试验的结果。其中：CF 表示蠕变-疲劳试验;σmax为最大应力；f为加载频率；Nf,exp为疲劳寿命的试验值；Tc为蠕变-疲劳时间。

3 P92钢的蠕变-疲劳寿命可靠性模型

3.1 P92钢的蠕变-疲劳寿命模型

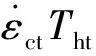
表2 P92钢在600 ℃不同试验条件下的蠕变-疲劳试验结果Tab.2 Creep-fatigue test results for P92 steel at 600 ℃under different experimental conditions

表3 P92钢600 ℃下蠕变-疲劳半寿命时的应变能密度Tab.3 Strain energy densities at half-life of creep-fatigue tests for P92 steel at 600 ℃

将表3的试验数据分成2组，第1组保载时间小于1.5 h，即CF01、CF02、CF03、CF05、CF06和 CF07，第2组保载时间为1.5 h，即CF04、CF08和CF09。利用第1组数据，根据式(3)拟合出应变能密度与蠕变-疲劳寿命的关系，如图5所示。将第1组蠕变-疲劳寿命的相关数据与式(16)的预测寿命进行比较，结果见图6中圆形数据点。

(16)

由图6可知，P92钢蠕变-疲劳寿命预测值与试验值的比值为0.706 44～1.347 10。

将第2组应变能密度的相关数据代入式(16)，预测在该试验条件下的蠕变-疲劳寿命，并与试验数据进行比较，结果见图6中矩形数据点，两者比值近似于1，预测效果较好。由此可知，对于P92钢，能够利用保载时间较短工况下的蠕变-疲劳寿命预测保载时间相对较长工况下的蠕变-疲劳寿命。

3.2 P92钢蠕变-疲劳寿命的P-Δup-Nf曲线

由式(16)可知，P92钢蠕变-疲劳寿命预测模型中A=2.694×107，m=1.082，将m设为定值，由式(4)计算不同试验条件下的lgAi，结果见表4。

图6 P92钢蠕变-疲劳寿命的试验值与预测值的比较Fig.6 Comparison of creep-fatigue life between experimental data and predicted values for P92 steel

表4 不同试验条件下的 lg AiTab.4 Values of lg Ai under different test conditions

随机变量lgA的标准差为：

(17)

因此，P92钢的P-Δup-Nf曲线为：

(18)

3.3 P92钢的蠕变-疲劳寿命可靠性模型

3.3.1 应变能密度的概率密度函数

假设在蠕变-疲劳试验过程中P92钢真实应力的最大值服从正态分布，即

(19)

由式(2)可知，应变能密度也服从正态分布。

(20)

可利用连续型随机变量函数的期望和方差推导计算式(20)中应变能密度的均值与方差：

(21)

(22)

将表3中的数据代入式(21)和式(22)，可以得到不同工况下P92钢应变能密度的概率密度函数，如图7所示。不同试验条件下应变能密度的均值与标准方差见表5。

3.3.2 蠕变-疲劳寿命的概率密度函数

基于P92钢的P-Δup-Nf曲线，根据式(9)和式(10)，lgNf的均值与方差为：

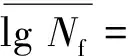
(23)

图7 P92钢在不同试验条件下的应变能概率密度函数Fig.7 Probability density functions of strain energy density for P92 steel under different test conditions

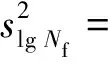
0.2×(i-1)]2=0.022 000

(24)

式中：μPi的取值范围为[-3,3]，为了确保样本数据足够多，等间距取31个值。

P92钢蠕变-疲劳寿命的概率密度函数为：

(25)

根据前文不同试验条件下P92钢应变能密度的均值，结合式(25)，P92钢在不同试验条件下蠕变-疲劳寿命的概率密度函数曲线如图8所示，其均值见表5。将由蠕变-疲劳寿命预测模型得到的疲劳寿命均值与P92钢试样在不同试验条件下的疲劳寿命相比，预测精度为[0.7,1.4]，随着保载时间的增加，预测精度约为95%。

表5 P92钢的蠕变-疲劳寿命可靠性分析Tab.5 Reliability analysis of creep-fatigue life for P92 steel

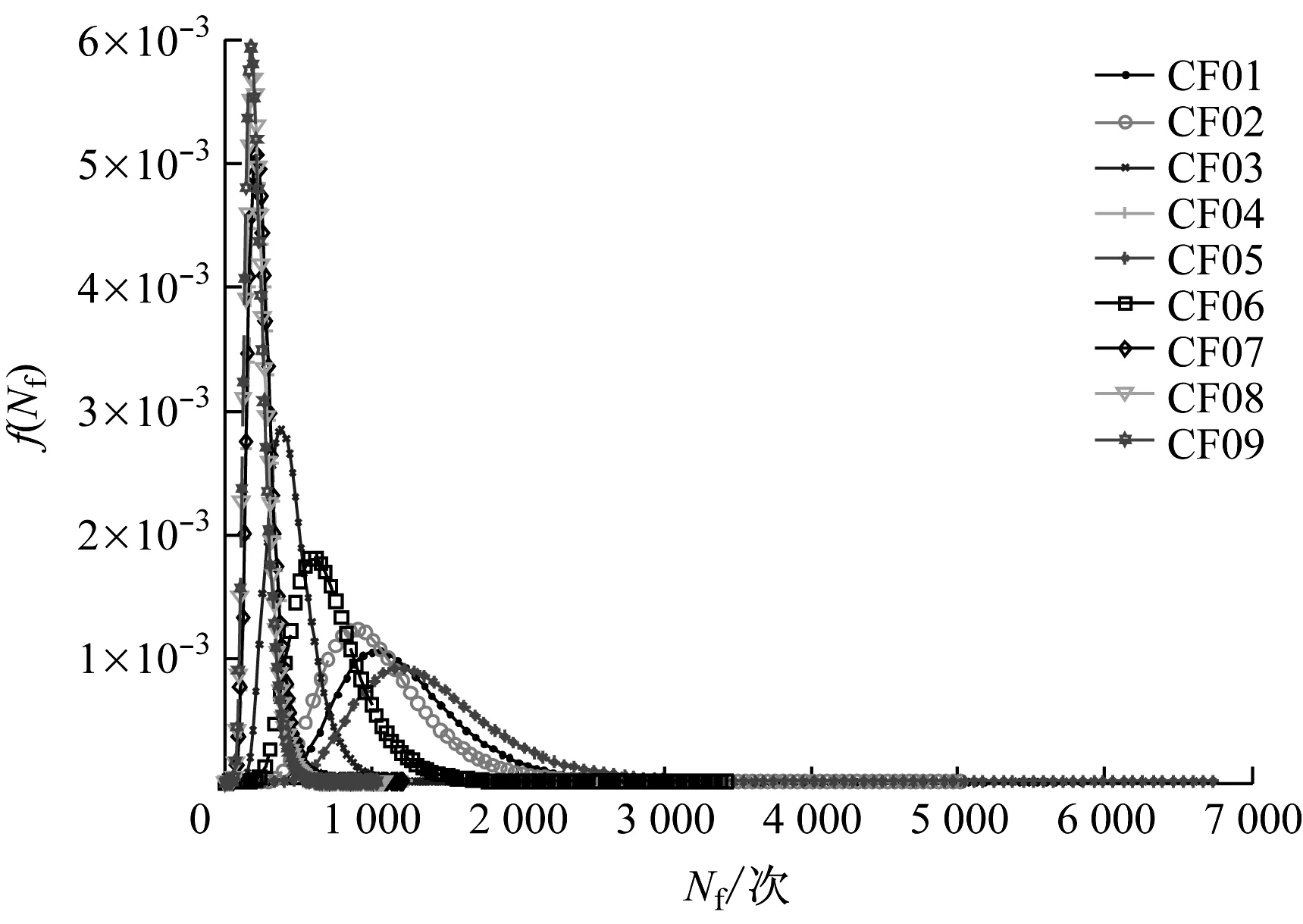
图8 P92钢在不同试验条件下蠕变-疲劳寿命的概率密度函数Fig.8 Probability density functions of creep-fatigue life for P92 steel under different test conditions

3.3.3 蠕变-疲劳寿命的可靠性分析模型

将P92钢的蠕变-疲劳寿命和应变能密度的概率密度函数代入式(15)，得到其蠕变-疲劳寿命可靠性分析模型。

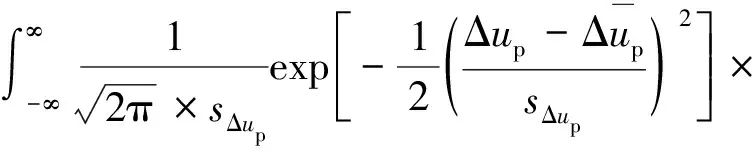
(26)

根据该可靠性模型计算P92钢蠕变-疲劳寿命为均值时的可靠度，结果均近似0.5，从而验证了该可靠性模型的合理性。

基于此模型，可以分析P92钢在某蠕变-疲劳寿命时的可靠度，以及在某可靠度下的蠕变-疲劳寿命。利用该模型分析了可靠度为99%时不同试验条件下P92钢的蠕变-疲劳寿命，此时寿命约为蠕变-疲劳寿命均值的43%。

4 结 论

(1) 提出了不同可靠度下应变能密度与蠕变-疲劳寿命的关系曲线(P-Δup-Nf曲线)，并基于P-Δup-Nf曲线推导出蠕变-疲劳寿命的可靠性分析模型。

(2) 开展了P92钢在600 ℃下的蠕变-疲劳试验，并分析了半寿命处的蠕变应变和加卸载弹性模量等。

(3) 基于试验数据及结果，研究了基于应变能密度的P92钢蠕变-疲劳寿命模型及P-Δup-Nf曲线，推导并验证了P92钢蠕变-疲劳寿命可靠性分析模型，可用于分析P92钢在某蠕变-疲劳寿命时的可靠度以及某可靠度下的蠕变-疲劳寿命。

(4) P92钢蠕变-疲劳寿命可靠性模型的疲劳寿命预测精度为[0.7,1.4]，且随着保载时间的增加，预测精度约95%；可靠度为99%时疲劳寿命约为其平均寿命的43%。