应用于气动弹性剪裁的大型风力机叶片弯扭耦合性能研究

刘宇航， 王渊博， 李 春， 孙 瑞， 郝文星

(上海理工大学 能源与动力工程学院， 上海 200093)

随着传统化石能源枯竭及其引发的环境污染问题愈发严重，风能作为可再生绿色能源逐渐得到青睐[1]。在逐步开发海上风场的大环境下，为提高风能转化效率、捕获更多风能和降低度电成本，风力机的大型化已成为风电发展的必然趋势[2]。然而，叶片大型化必然会使叶片质量增加，导致疲劳载荷和惯性载荷增加，使得变桨控制更加困难，并会缩短机组寿命[3]。随着叶片沿展向和弦向尺寸的增加，会导致叶片刚度降低，工作期间挠度提高，增大叶片与塔架发生碰撞的可能性[4]。由于风电由陆地逐渐向海上发展，气动载荷、重力载荷、波浪载荷和惯性载荷等相互耦合作用，复杂多变的海上风力机在役环境导致叶片结构的安全性需要进一步提高[5]。新型风力机叶片具有弯扭耦合性能，其原理是利用叶片大型化引起的柔性减小叶片内部载荷密度，提高叶片抗疲劳性能，可以随风速变化而改变叶片扭转角，合理的扭转增大了机组的工作风速范围，提高了获能效率[6]。

国内外学者对弯扭耦合叶片开展了初步研究。Zayas等[7]设计并加工出9 m的弯扭耦合叶片，叶片在外载荷作用下产生的扭转变形可起到卸载能量的效果。Ashwill[8]设计了长为27 m的弯扭耦合叶片，与普通叶片相比，在相同工况下弯扭耦合叶片可提高12%的能量输出。周邢银等[9]将风力机叶片简化为对称非均匀铺层层合板梁，研究了耦合区域对叶片弯扭效应的影响。胡国玉等[10]通过FAST软件计算并实现了5 MW风力机叶片表面气动载荷的加载，分析了静态下弯扭耦合对叶片性能的影响。

考虑到上述研究未将铺层参数、叶片结构和气动载荷三者耦合，笔者以5 MW风力机叶片为研究对象，采用参数化建模方法，建立叶片全尺寸三维有限元壳模型，基于AnsysWorkbench平台，通过改变铺层结构实现叶片气动弹性剪裁(即改变叶片铺层控制结构的弹性变形)，并采用CFD方法加载气动力，分析叶片扭转变形的物理机制，探究铺层结构对叶片弯扭性能的影响。

1 叶片弯扭耦合效应及复合材料铺层

在风力机运行过程中，叶片受气动载荷作用发生挥舞弯曲，且弯曲幅度随风速的增大而增大。在极端风况下，如果叶片仍未达到失速状态，增大升力和攻角会使叶片所受气动载荷剧增，甚至大于失速时的气动载荷，故易出现破坏性冲击。弯扭耦合效应是指叶片发生弯曲变形的同时沿叶片展向环向发生扭转变形，如图1所示，进而改变叶片攻角[11]。根据叶素动量理论，攻角变化直接影响叶片运行过程中的合速度。叶片在达到顺桨状态的过程中，弯扭耦合效应可降低叶片所受载荷，延长机组寿命，扩大风力机的工作风速范围，增加机组获能。

复合材料因其比强度高、耐疲劳和设计性强等优点，近年来被广泛用于风力机叶片。为保证强度和刚度需求，常规叶片复合材料大多沿弦线面交叉对称进行铺设[12]。为实现弯扭耦合效应，基于气动弹性剪裁[13]将叶片纤维按偏轴镜像对称方式进行铺设，纤维铺设方向为S，如图1(a)所示。将叶片蒙皮沿弦线面分为2个部分，吸力面和压力面蒙皮纤维方向与叶片展向(z轴正方向)夹角为θ，且以弦线面呈镜像对称。叶片在气动载荷作用下发生变形，在叶片展向产生弯曲变形，弯曲角为ω，如图1(b)所示。沿叶片展向，由于铺层为偏轴镜像对称，叶片具有弯扭耦合性能，发生弯曲的同时出现扭转变形，扭转角为φ，如图1(c)所示。

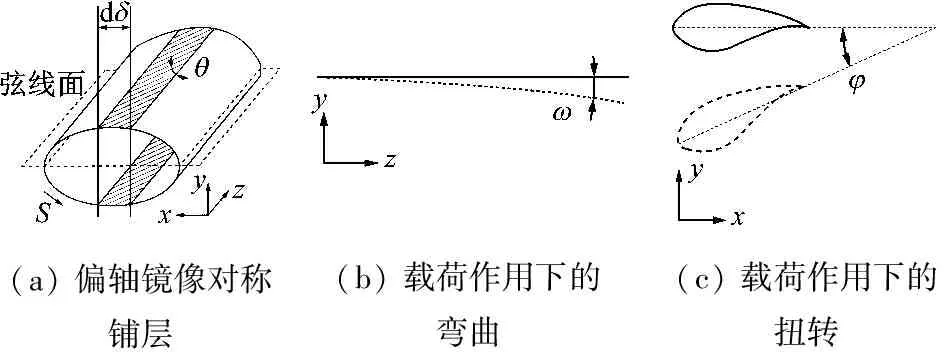
(a) 偏轴镜像对称铺层(b) 载荷作用下的弯曲(c) 载荷作用下的扭转

图1 弯扭耦合叶片示意图

Fig.1 Schematic diagram of the bend-twist coupling blade

为描述叶片弯扭耦合程度，Walsh[14]提出耦合系数ε为：

ε=φtip/ωtip

(1)

式中：φtip为叶尖扭转角；ωtip为叶尖角度。

通常采用截面刚度法和节点位移法[15]计算耦合系数。截面刚度法是将叶片简化为悬臂梁模型，通过弯曲刚度矩阵和扭转刚度矩阵求解耦合系数。由于大型风力机叶片是一种多翼型复杂曲面薄壁结构，截面刚度法难以精确求解，甚至无法求解出设计叶片的耦合系数。节点位移法可通过建立三维叶片复合材料有限元模型，求解成型叶片在载荷作用下的节点位移，进而得到耦合系数。节点位移法对叶片耦合系数的描述不仅考虑了各截面刚性位移和自身变形，还考虑到叶片的长度和截面耦合。随着计算机性能的提高，运算速度和计算精度可以满足设计误差的要求，故笔者采用节点位移法。

2 叶片模型

2.1 叶片建模

由美国可再生能源实验室(NREL)的公开数据建立NREL 5 MW风力机叶片模型[16]。叶片沿展向分为叶根区域、过渡区域和气动区域，为兼顾气动和结构性能，分别采用荷兰DU系列翼型和美国NA64翼型，如图2所示。叶片总长为61.5 m，最大弦长为4.7 m，额定转速为12.1 r/min，额定风速为11.4 m/s。图2给出了5 MW风力机叶片壳模型。在叶根位置施加固定端约束，采用SHELL99单元划分叶片网格后，网格单元数为62 164，节点数为62 468，如图3所示。

图2 叶片壳模型Fig.2 Model of the blade shell

图3 叶片网格划分Fig.3 Meshing of the blade

为使叶片工作时达到最佳攻角，获得最佳风能效率，参考文献[17]将叶片设计为预扭叶片。如图4所示，在气动区域前，翼型扭转角为13.308°，此后沿叶片展向扭转角逐渐减小，在叶尖处扭转角为0°；叶根弦长为3.542 m，由叶根向叶尖方向弦长先增大后减小，在截面相对位置约0.23处达到最大值，在叶尖处为最小值。

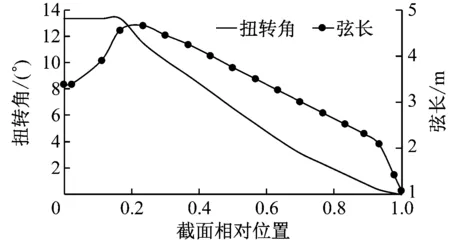
图4 叶片扭转角和弦长分布Fig.4 Chord schedule and twist angle distribution of the blade

2.2 叶片材料及铺层结构

借鉴文献[16]中叶片的铺层和材料参数，设计的5 MW叶片截面铺层结构由5个区域组成，分别为前缘夹心区域a、后缘加强区域b、后缘夹心区域c、梁帽区域d和腹板区域e，如图5所示。

胶衣提供光滑的外表面，减少因加工过程而产生的粗糙度，并且可保护结构层材料不被外环境介质侵蚀。单向布由玻璃纤维组成，用于加强梁帽区域d和后缘加强区域b。双向布由±45°的玻璃纤维组成，用于腹板区域e的外层铺设。三轴向布由0°和±45°铺层的玻璃纤维构成，用于蒙皮和叶根铺层。前缘、后缘和腹板采用三明治夹心结构，夹心材料为各向同性的泡沫，以提高叶片在该区域的抗失稳性。铺层材料力学参数[18]如表1所示，其中Ex为纵向弹性模量，Ey为横向弹性模量，v为泊松比，Gxy为剪切模量。

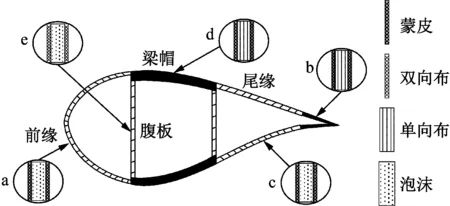
图5 叶片截面及铺层Fig.5 Cross section and laminated structure of the blade

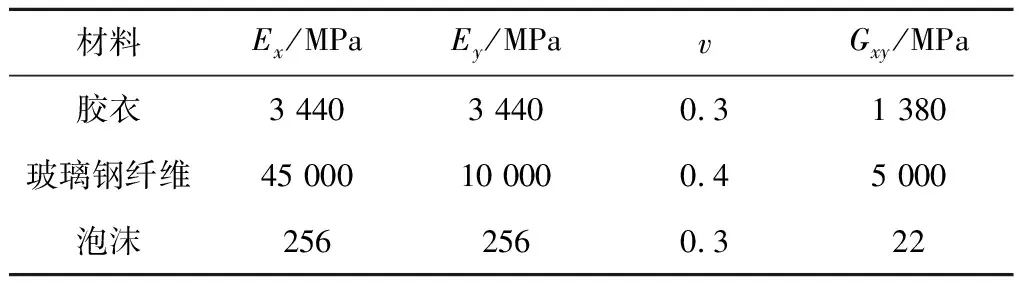
表1 铺层材料力学参数Tab.1 Mechanical properties of ply materials

2.3 叶片模型验证

为研究蒙皮偏轴夹角θ对叶片整体弯扭性能的影响，以15°为间隔，θ由0°增大至90°，可实现叶片的弹性剪裁。通过FAST前处理软件Precomp计算弯扭耦合叶片的挥舞刚度和摆振刚度，结果如表2和表3所示。沿叶片展向，越靠近叶尖，叶片挥舞刚度和摆振刚度均越低。这是因为叶片为悬臂梁结构，靠近叶根位置处受到的载荷较大，铺层厚度较大，靠近叶尖位置铺层厚度较小。同一叶片截面处，随着θ的增大，挥舞刚度明显降低，摆振刚度略降低，这是因为复合材料具有显著的各向异性，沿纤维方向的弹性模量远大于其他方向的弹性模量。当θ增大时，叶片刚度降低，挥舞刚度和摆振刚度均降低。将Precomp计算结果与文献[16]中技术文件提供的数据进行对比，发现数值吻合，表明所设计的叶片复合材料铺层三维模型精度较高，符合数值模拟要求。

3 气动载荷

利用CFD方法求解叶片气动载荷，针对NREL5 MW三叶片风力机轴对称的特点，计算域选取实际区域的1/3，可使网格单元数和计算量大幅减少。计算域如图6所示，以叶片长度R为基准，叶片距计算域入口为2R，距离出口为5R，计算域半径为5R。计算域入口边界条件为速度进口，其值为NREL 5 MW风力机的额定风速11.4 m/s；出口为压力出口，其值为1个标准大气压；上方弧面设为零梯度边界条件；叶片表面设为壁面边界条件；剩余2个矩形面设为周期边界条件，两侧网格节点一一对应，紧贴周期边界一侧计算域外“镜像单元”的信息由紧贴另一侧周期边界计算域内的单元提供。网格划分参照文献[19]，流场计算域网格如图7所示。

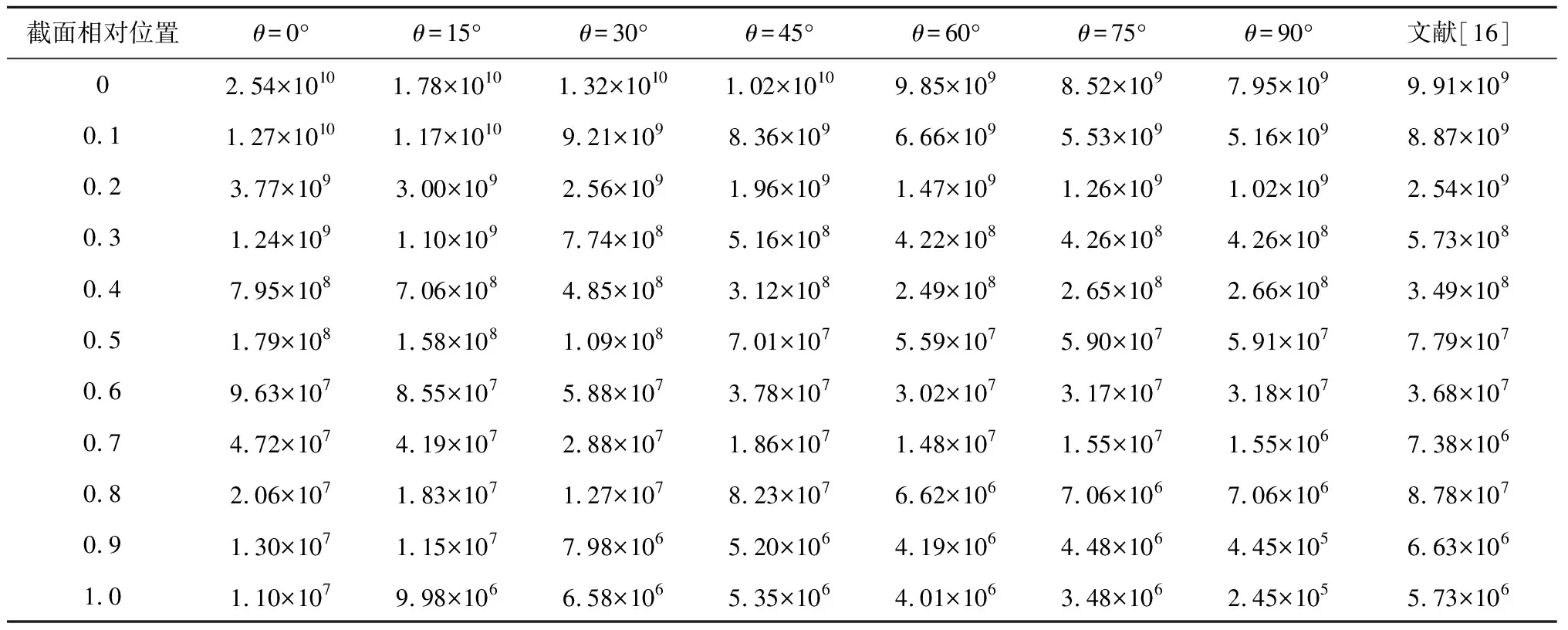
表2 叶片挥舞刚度Tab.2 Flapwise stiffness of the blade

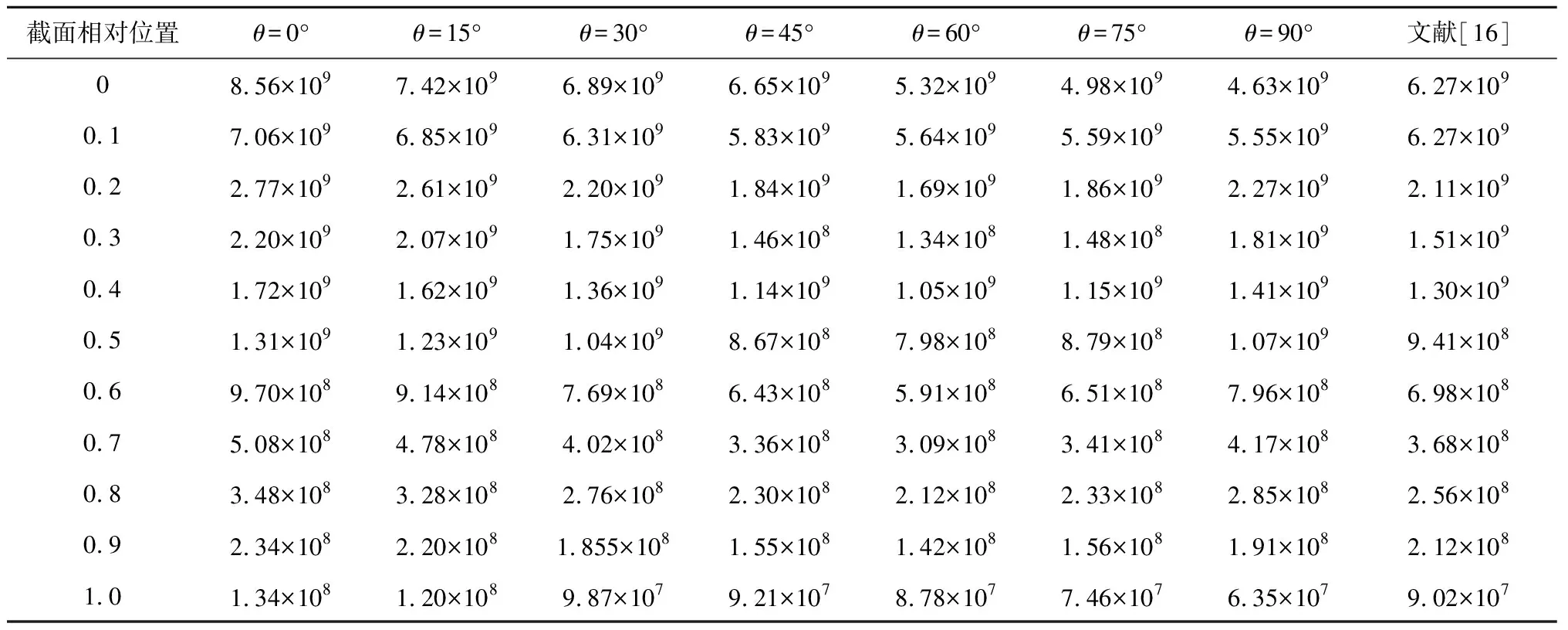
表3 叶片摆振刚度Tab.3 Edgewise stiffness of the blade

对于多数大升力的问题，S-A湍流模型和SSTk-ω湍流模型针对气动性能的模拟均与实验值较接近[20]，但SSTk-ω湍流模型能更好地预测由压力引起的翼型流动分离，因此使用SSTk-ω湍流模型来模拟叶片具有更高的精确性。

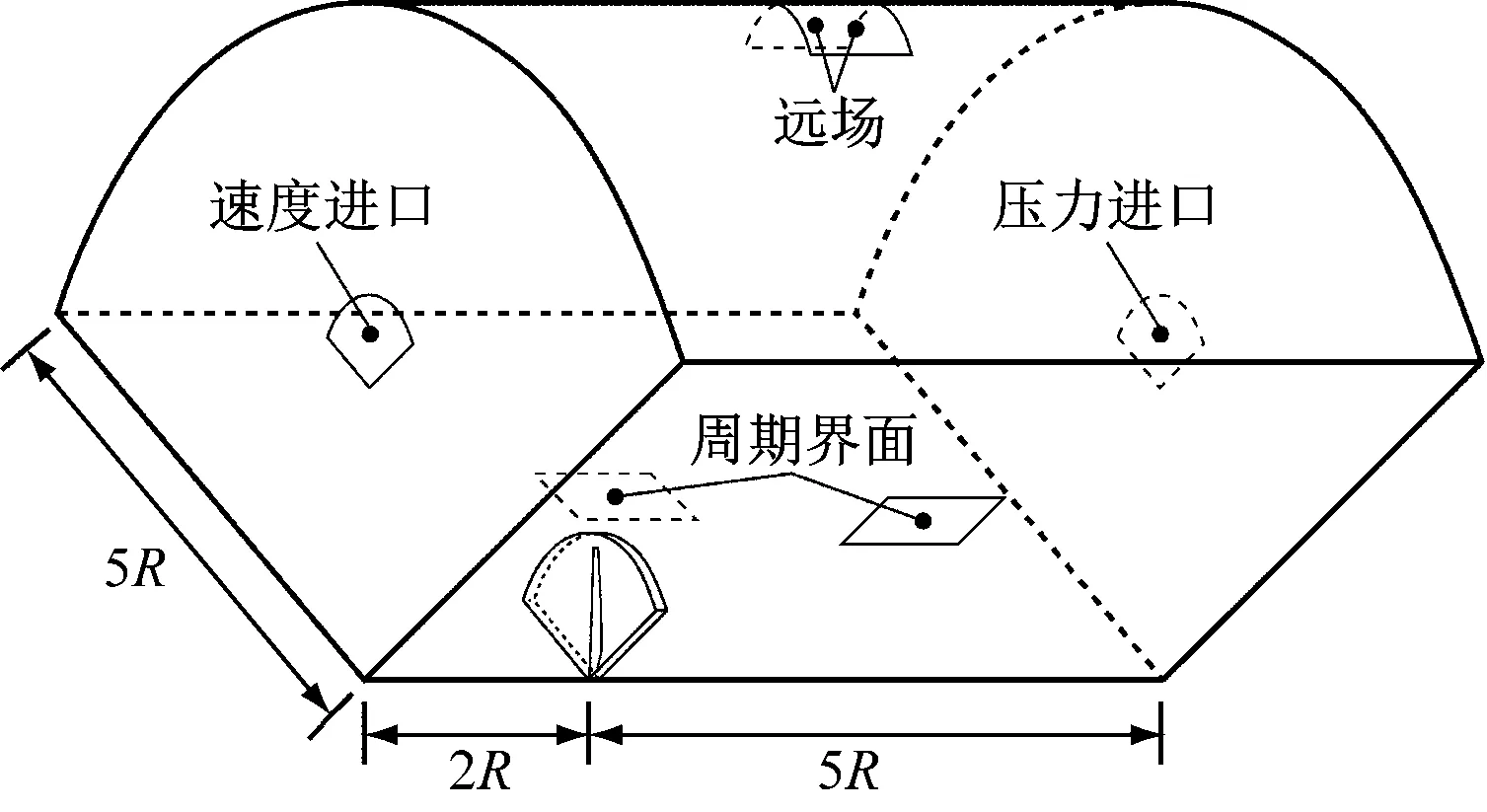
图6 流场计算域及边界设置Fig.6 Setting of the flow field calculation domain and boundary

流场计算结果如图8所示。同一截面处叶片前缘和尾缘压力较大，梁帽处压力较小。沿叶片展向，叶片前缘位置载荷逐渐增大，而梁帽位置载荷逐渐减小。叶片吸力面受到的载荷大于压力面，两者差值导致形成叶片升力，也造成叶片发生弯曲和扭转变形。

(a) 外流场网格(b) 内流场网格

图7 流场计算域网格

Fig.7 Meshing of the fluid domain

(a) 压力面

(b) 吸力面图8 额定工况下叶片表面的气动载荷Fig.8 Aerodynamic load on the blade surface under rated condition

4 弯扭耦合特性分析

将额定工况下叶片表面的气动载荷加载到设计的三维壳有限元模型叶片上，改变蒙皮偏轴夹角，采用节点位移法，计算得到不同弯扭耦合叶片的弯曲角和扭转角，如图9所示。

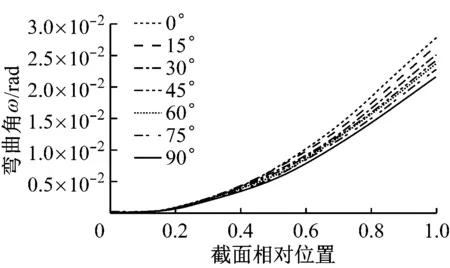
(a) 弯曲角

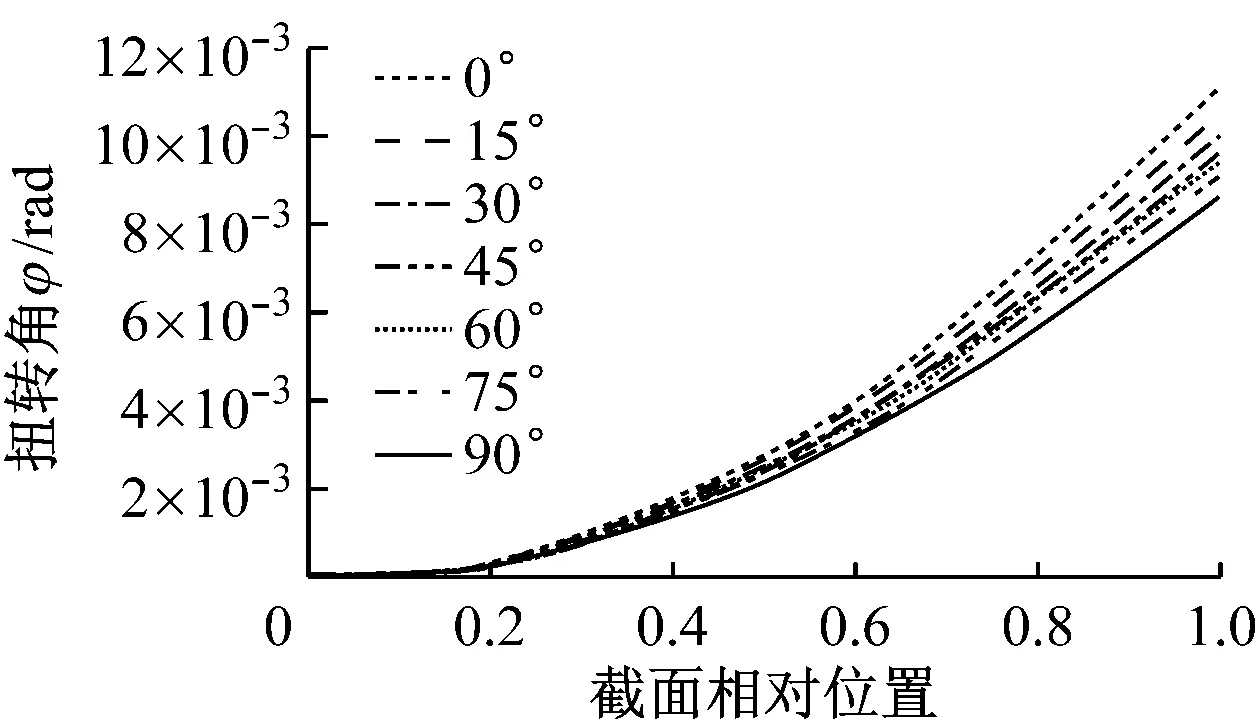
(b) 扭转角图9 弯扭耦合叶片弯曲扭转变形Fig.9 Deformation of bend-twist coupling blades

由图9(a)可知，叶片根部几乎不发生变形，叶尖处变形最大。弯曲变形量沿叶片展向逐渐增加，与蒙皮偏轴夹角θ无关。弯曲变形量与截面相对位置为非线性相关，在截面相对位置0.3～1之间，叶片弯曲角度与距叶根的相对位置呈非线性相关。相同截面相对位置处，弯曲变形量随蒙皮偏轴夹角θ的增大而增大，当蒙皮偏轴夹角与叶片展向垂直时，弯曲角度达到最大。由图9(b)可知，叶根部位几乎不发生扭转，叶尖部位扭转最为明显。沿叶根向叶尖方向扭转角增大，相同截面相对位置处蒙皮偏轴夹角θ越大，扭转变形越大，叶尖扭转角达到1.5×103rad。

蒙皮纤维镜像对称铺设，导致叶片具有弯扭耦合性能。铺层厚度沿叶片展向逐渐减小，叶片截面挥舞刚度和摆振刚度降低，故靠近叶尖处弯扭变形越明显。蒙皮偏轴夹角由0°变化到90°时，在弹性剪裁作用下叶片展向等效刚度降低，弦线方向等效刚度提高，因此相同截面处弯曲角和扭转角均减小。

由弯扭耦合系数的定义计算出各设计叶片叶尖处的耦合系数，如图10所示。

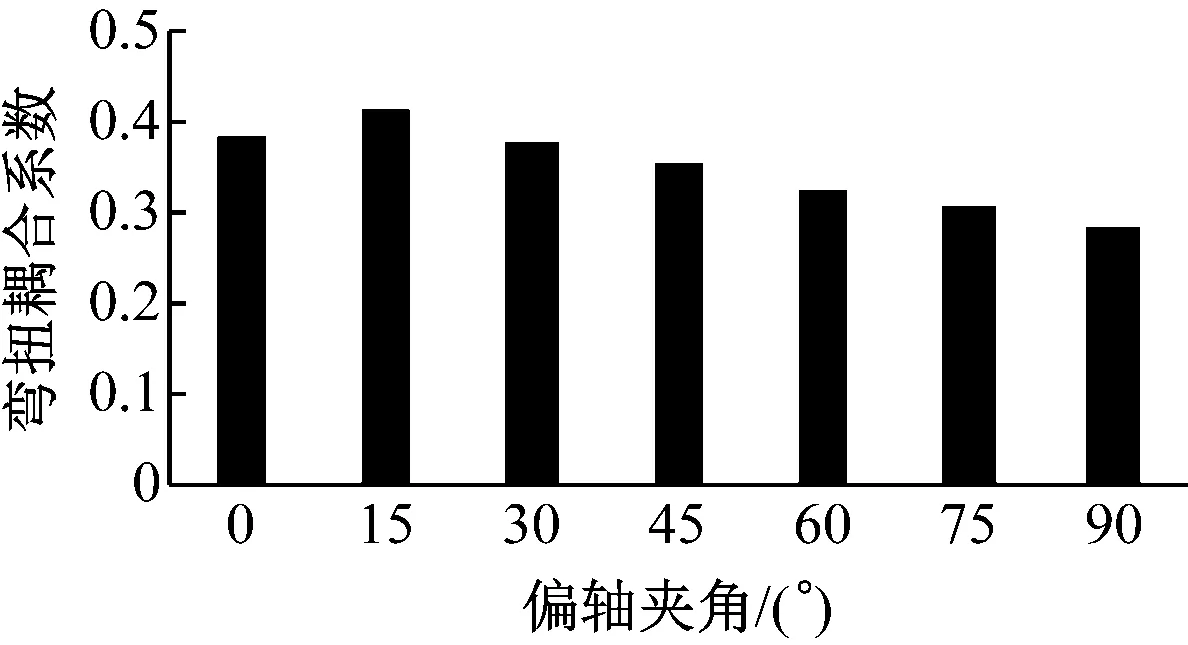
图10 不同弯扭耦合叶片的弯扭耦合系数Fig.10 Bend-twist coupling coefficients of different blades

由图10可知，不同弯扭耦合叶片的弯扭耦合系数不同，且差异显著。随着偏轴夹角的增大，弯扭耦合系数先增大后减小，偏轴夹角为15°时弯扭耦合系数最大，其值为0.426；偏轴夹角为90°时弯扭耦合系数最小，其值为0.291。由于蒙皮纤维镜像对称布置，叶片吸力面与压力面均发生弯扭耦合效应，且扭转方向相同，在外载荷作用下叶片同时发生弯曲变形和扭转变形。随着蒙皮偏轴夹角(<15°时)的增大，叶片扭转刚度的变化量大于弯曲刚度的变化量，弯扭耦合系数增大；继续增大蒙皮偏轴夹角(≥15°时)，叶片弯曲刚度的变化量大于扭转刚度的变化量，弯扭耦合系数减小。

5 结 论

(1) Ansys复合材料模块可实现复杂的大型风力机叶片结构铺层，建立的叶片模型精度高、误差小。通过CFD方法获得的叶片气动载荷能细致描述叶片表面的受力情况，可提高数值模拟精度。

(2) 随着蒙皮偏轴夹角的增大，叶片弯扭耦合系数先增大后减小，蒙皮偏轴夹角为15°时叶片具有足够的挥舞刚度和摆振刚度，且弯扭耦合性能最佳，弯扭耦合系数达0.426。