集装箱公铁联运定价策略的博弈分析

张 桐，毛保华*,b，曾 玮，麻存瑞，张思佳

(北京交通大学a.城市交通复杂系统理论与技术教育部重点实验室；b.中国综合交通研究中心，北京100044)

0 引言

“一带一路”战略的提出为我国多式联运发展带来了历史性的契机与挑战，集装箱公铁联运作为海铁联运向内陆延伸的重要运输方式，一直以来发展缓慢.近年来，国家出台了系列宏观政策以推动多式联运发展.其中，《“十三五”铁路集装箱多式联运发展规划》中提出以健全运价调节机制，通过不断优化运价方案，来实现企业收益最大化.为充分发挥公铁联运运输优势，集装箱公铁联运运价调节需要充分结合市场供求关系与竞争形势变化，以实现企业自身利益最大化.

国外对于多式联运策略的研究较多，并开发了诸如 NODUS[1]、LAMBIT[2]、SIMBA[3]、Macro-scan[4]等工具对制定策略进行了效果评估.关于定价策略的制定，Labbe等[5]考虑定价策略对托运人的影响构建了双层规划模型，上层为承运人收益最大化模型，下层为托运人运输方式选择模型，并在此基础上设计了基于网络的多式联运定价模型.国内关于多式联运定价策略的研究较少，张戎等[6]在搜集整理2000年以后46篇文献研究的基础上，分析了托运人货运服务选择影响因素，并构建了托运人货运服务选择非集计模型；唐继孟[7]通过刻画集装箱公铁联运与公路直达运输作业流程建立了基于全过程的公铁联运广义费用函数，并采用MNL模型构建了公铁联运竞争力模型；冯芳玲等[8]基于Hoteling模型分析了公路货运和铁路货运在运价及服务竞争方面长期反复的博弈关系；张小强等[9]考虑了客户的广义费用和铁路运营企业收益，构建了竞争环境下的铁路快捷货运定价模型.

国内外对于集装箱公铁联运定价策略的研究较少，多数研究围绕铁路与公路货物运输服务竞争关系构建定价模型.因此，本文在前人研究的基础上，从集装箱货物运输作业全过程角度出发分析托运人运输方式选择的影响因素，并基于博弈论思想研究单一起讫点集装箱公铁联运的定价策略.

1 运输方式选择影响因素分析

在集装箱运输方式选择方面，影响托运人运输方式选择的因素主要包括两个：一是运输全过程所消耗的运输时间，二是运输全过程需要支付的运输费用.根据运输方式效用理论，托运人将选择运输方式所付出“综合代价”更小的运输方式进行货物运输[6-7].

1.1 集装箱全过程运输时间分析

(1)集装箱公路直达运输时间.

集装箱公路直达运输全过程包括发送端运输时间、干线运输时间、到达端运输时间.发送端运输时间包括订单处理时间、空箱配送时间、货物装箱时间th1，以及发送端市区运输时间；到达端运输时间包括到达端市区运输时间、集装箱掏箱时间th2；干线运输时间.集装箱公路直达运输时间为[7,10]

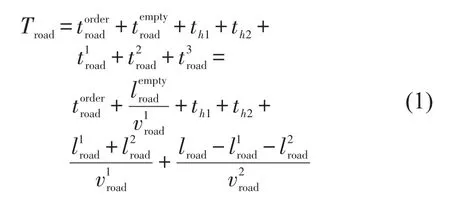
(2)集装箱公铁联运时间.

集装箱公铁联运运输全过程包括前期运输时间、铁路内部运输时间、后期运输时间.前期运输时间包括订单处理时间，空箱配送时间，货物装箱时间th1，重箱运回时间，重箱进站手续办理时间tp；铁路内部运输时间由公铁联运组织模式决定，主要包括3类运输时间，即短途小运转列车运输时间、中长途普通集装箱班列运输时间和长途集装箱班列运输时间；后期时间包括重箱配送时间及货物掏箱时间th2.集装箱公铁联运全过程运输时间为[7,10]

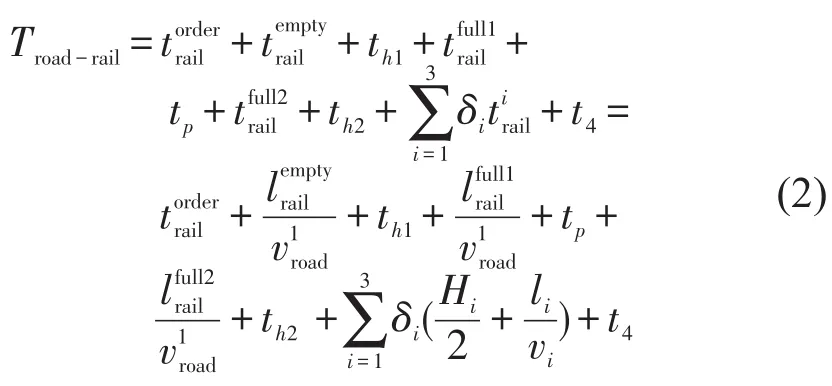
1.2 集装箱运输费用分析

(1)集装箱公路直达运输费用.

集装箱公路直达运输总费用Croad由基本运费croad、装掏箱费用ch，以及车辆过桥、过收费公路所产生的额外费用组成.集装箱公路直达总运费为

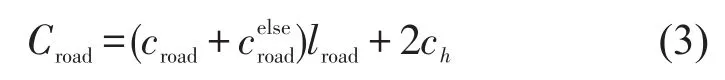
(2)集装箱公铁联运运输费用.

集装箱公铁联运总运费由接取送达费用、铁路站间运输费用，以及装掏箱费用组成.集装箱公铁联运总费用为

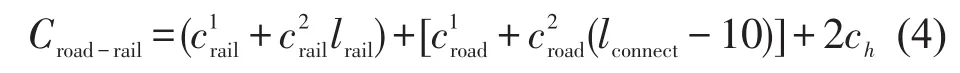
式中：Croad-rail为集装箱公铁联运总费用(元/(TEU⋅km))；为集装箱铁路发到基价(元/TEU)；为集装箱铁路运行基价(元/(TEU⋅km))；lrail为集装箱铁路运输里程(km)；为公路接驳运输起码里程费用(元/TEU)；为公路接驳运输超过起码里程运输费率(元/(TEU⋅km))；lconnect为公路接驳运输距离(km).

2 定价博弈模型构建

2.1 竞争力模型构建

以随机效用最大化理论为基础，随机效用值由确定效用Vm及随机效用εm组成，假设随机效用εm服从Gumbel分布，则托运人运输方式选择概率MNL模型为

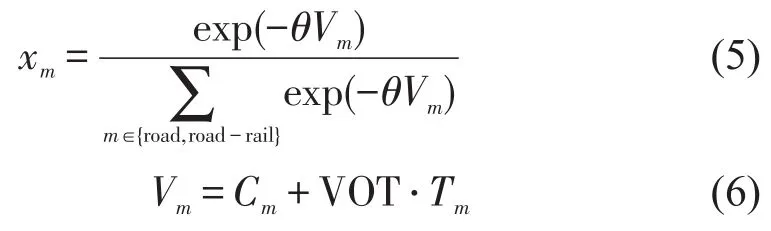
式中：θ为需要标定的参数，可理解为托运人感知误差；Cm为第m种运输方式托运人需要支付费用(元/TEU)；Tm为第m种运输方式运输时间(h)；VOT为集装箱货物时间价值(元/(TEU⋅h)).

2.2 运输方式收益计算

在市场经济条件下，可将公路直达运输承运公司、短途物流企业及铁路运输企业看成3个独立企业进行分析，不考虑其他收入与支出，每种运输方式收益由集装箱箱数及运输费率共同决定.

集装箱公路直达运输由长途物流企业承运，其收益为

集装箱公铁联运由短途物流企业及铁路运输企业共同承担.其中，短途物流企业收益为

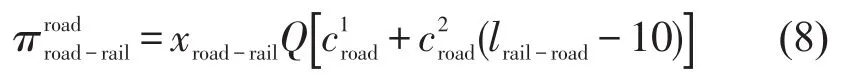
铁路运输企业收益为

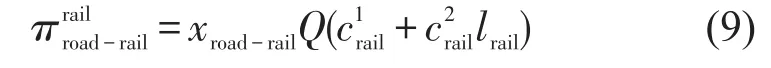
式中：Q为起讫点间集装箱需求总量(TEU)；πroad为公路直达运输收益(万元)；为公铁联运模式铁路运输企业收益(万元)；为公铁联运模式短途接驳运输收益(万元).

2.3 纳什博弈模型

集装箱公路直达运输基本运价、公铁联运中接驳费率及铁路运价的调整均会影响托运人运输方式选择.本文假设以铁路运价调整作为公铁联运定价的主体策略，铁路运输收益最大化模型为

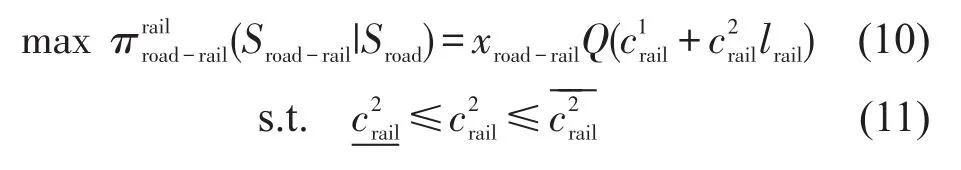
式(10)最大化了公铁联运铁路运输收益，式(11)定义了集装箱铁路运行基价范围.

若存在策略使得其他运输企业均不能通过改变运费来提升收益，该策略为满足主体策略的纳什均衡点.为便于模型描述，Sroad(croad)、分别表示公路直达运输定价策略及公铁联运定价策略.

式(12)和式(13)分别最大化了公路直达运输与短途物流运输收益，式(14)和式(15)分别定义了公路直达运输与公路接驳运输运费范围.

3 博弈模型求解

本文借鉴双矩阵博弈纳什均衡划线法求解思路，设计模型求解过程如下.

Step 1构建定价策略集合.

将公路直达运输基价变量以0.1为步长构建公路直达运输离散定价策略集合；同理，构建公路接驳运输费率离散定价策略集合；构建铁路运行基价离散定价策略集合.

Step 2构建双矩阵博弈模型.

设置初始值i=1，构建的双矩阵博弈模型为

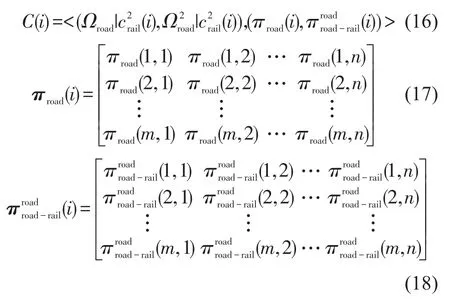
Step 3纯策略纳什均衡求解.

分别标记πroad(i)集合中每列元素中的最大值，集合中每行元素中的最大值.若存在1≤k0≤m，1≤j0≤n，使得式(19)成立，则双矩阵博弈模型C(i)存在纯策略纳什均衡解；若存在纯策略纳什均衡解且i＜r，则i=i+1，转至Step2；若不存在纯策略纳什均衡解，转至Step4.

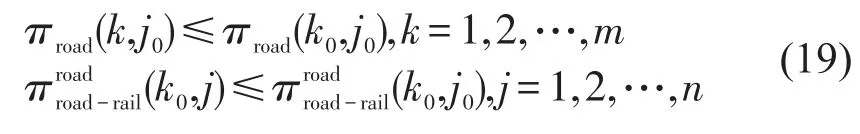
Step 4近似纳什均衡求解.

在不允许混合策略均衡的情况下，很多问题是没有均衡解的.因此，当不存在纯策略纳什均衡解时，采用近似纳什均衡的方法予以求解[11-12].

定义ε＞0，若存在1≤k0≤m，1≤j0≤n，使得式(20)成立，标记最小ε所对应的矩阵元素，则最小ε所对应的解即为近似纳什均衡解；若i＜r，则令i=i+1，转至Step2.

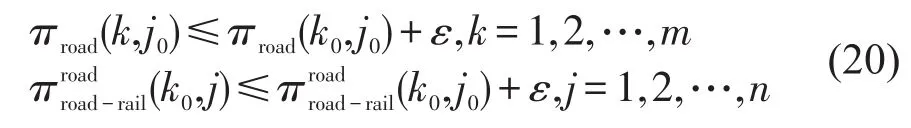
Step 5生成最优策略.

通过Step1～Step4的反复迭代，标记均衡解集合中使得铁路运输收益最大的定价策略，该策略即为通过数值模拟所得到的定价策略.

4 案例分析

4.1 案例背景

本文以A港至B地的集装箱运输作为案例进行分析.由于A港至B地运输距离较短，大部分集装箱运输为公路直达运输，公铁联运所占比例仅为8.3%.集装箱公路及公铁联运组织模式如图1所示[7].本文参考文献[7]所提供的公铁联运参数列表，标定竞争力模型参数θ为0.002.

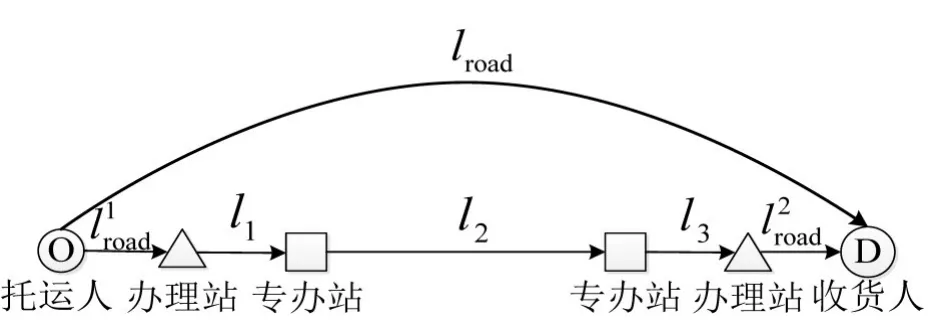
图1 集装箱运输组织模式示意图Fig.1 Schematic diagram of container transport organization mode

4.2 均衡结果分析

由于集装箱公铁联运主要由公路接驳运输与铁路干线运输两部分组成，因此公铁联运定价由短途物流企业及铁路运输企业共同决定，本文设计2种情景分析公铁联运定价策略.

情景A铁路运输企业近期不调整运价，短途物流企业通过调整运价提升运输收益.

情景B铁路企业制定运价调整策略，短途物流企业通过调整运价提升运输收益.

数值模拟计算中，公路直达运价croad在区间[4,10]取值，公铁接驳费率在区间[15,30]取值，铁路运价在区间[1,6]取值，均以0.1作为步长，根据设计算法进行求解，得到两种情景下的纳什均衡解，如表1所示.

表1 集装箱公路直达运输与公铁联运运输均衡定价及收益比较Table 1 Equilibrium pricing and earning comparison between road-only transport and RRIT

情景A铁路企业近期不调整运价.

当铁路运输企业保持原运输价格时，通过模型求得的公铁联运接驳费率为18.3元，公路直达运输运价为7.3元.从与现状的对比结果可以看出，通过价格调整公铁联运分担率增加了11.4%，公路直达运输收益增加了6.54%，公路接驳运输收益增加了1.18倍，铁路运输收益增加了1.37倍.

情景B铁路企业制定最优定价策略.

当短途物流企业间竞争日趋激烈时，铁路运输企业的定价策略将有所转变，此时铁路运输企业通过制定定价策略以获取最大收益.根据模型求解得到铁路运价为4.7元，公铁联运接驳费率为15元，公路直达运输运价为10元.从与情景A的对比结果可以看出，通过价格调整公铁联运分担率虽然有所下降，但铁路运输收益增加了38.4%.

4.3 货运距离对均衡解的影响

货运距离的变化会对运输方式的广义费用值产生影响，从而影响托运人货运方式的选择.因此，为进一步分析货运距离对定价策略的影响，以100 km为步长，选取100～1 000 km不同的货运距离用以对比分析，不考虑绕行系数及运输能力变化对结果的影响，假设其他参数不变，得到不同货运距离下的定价策略如表2所示.

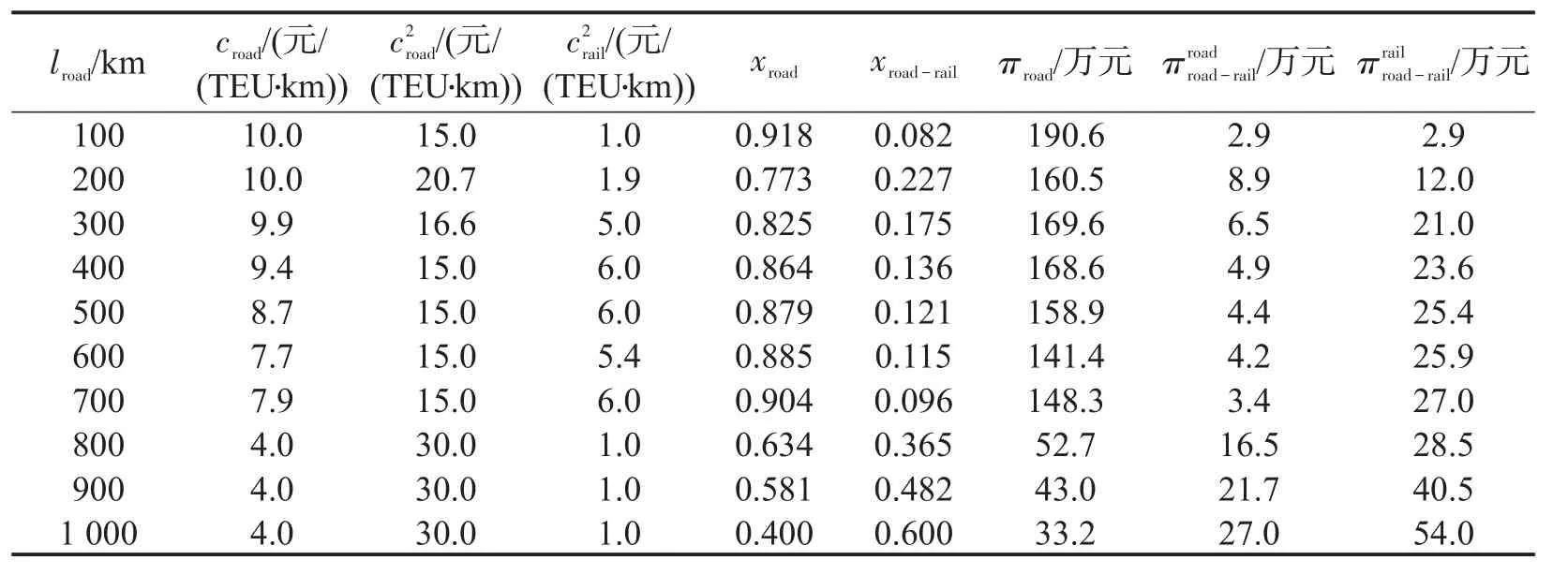
表2 不同货运距离下的定价策略Table 2 Pricing strategy under different shipping distances

由图2～图4可以看出，货运距离的变化对定价策略、货运分担率及企业运营收益均产生了一定影响.依据距离变化对三者的影响效果，可将货运距离分成3个区段，即短途(100～200 km)、中长途(200～700 km)和远途(700～1 000 km).

短途货运距离下，相较于公路直达运输而言，铁路集装箱运输不具备竞争优势，此时铁路集装箱运行基价在2.0元以下，在不考虑行业内部竞争的情况下，公路直达运输可以采用最大运价提供货运服务以获取最大收益.

中长途货运距离下，铁路集装箱运行基价在5.0～6.0元范围波动，公路接驳费率则以接近最低运价15.0元作为最优定价策略，公路直达运输基价则随着货运距离的增长而不断下降.由图3和图4可以看出，中长途货运距离下的公路直达运输仍具备明显优势，但由于定价策略的调整其运输收益随着距离的增长而呈现下降趋势；相反，铁路运输收益则呈现稳定上升趋势.

远途货运距离下，铁路集装箱运输优势明显，此时铁路企业可采用集装箱运行最小基价作为最优定价策略，公路直达运输企业则需采用最低运输基价以获取企业最大收益.由图3和图4可以看出，当货运距离超过700 km时，公路直达运输分担率及运输收益呈明显下降趋势；相反，集装箱公铁联运分担率及运输收益呈现显著上升趋势.

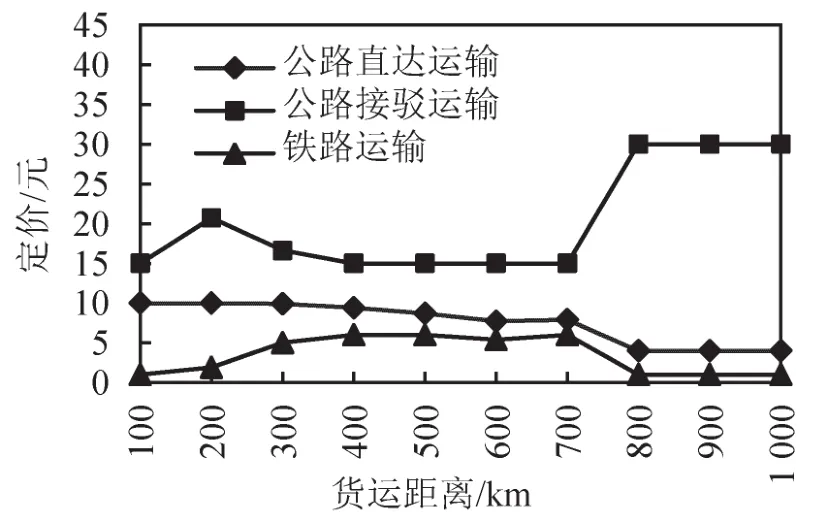
图2 不同货运距离下的最优定价Fig.2 Optimal pricing with different freight distances

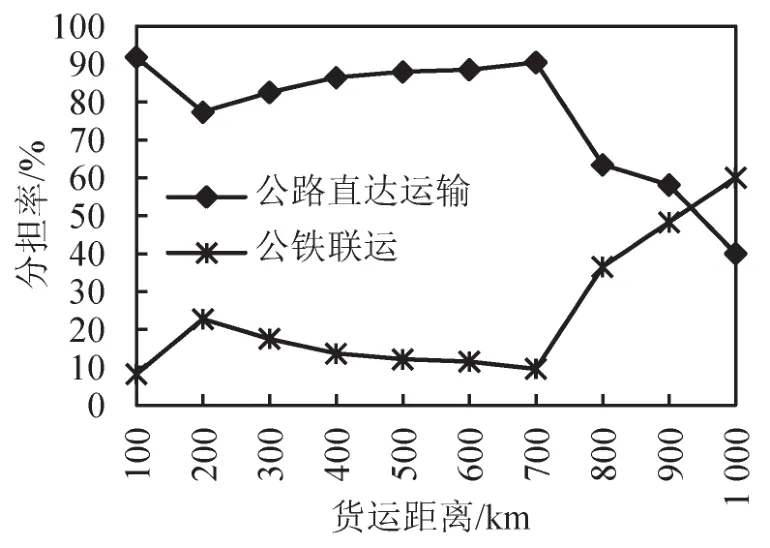
图3 不同货运距离下的货运分担率Fig.3 Freight ratios with different freight distances

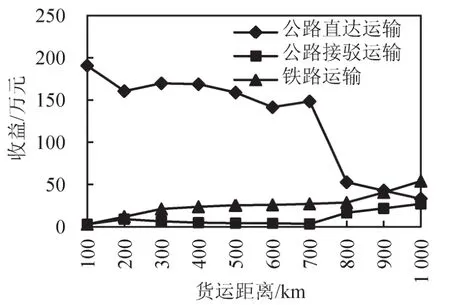
图4 不同货运距离下的收益Fig.4 Transportation revenue with different freight distances

5 结 论

本文基于博弈论思想对集装箱货物运输单一起讫点间公铁联运与公路直达运输定价策略进行了分析，得到如下主要研究结论：

(1)集装箱公铁联运运营初期，若铁路运价不进行调整，公路直达运输企业和短途物流企业可分别通过提升公路直达运价及降低接驳费率来提升企业收益.

(2)当短途物流企业间竞争日趋激烈时，即当公铁联运接驳运输条件可以充分满足时，铁路运输企业可通过制定定价策略以获取最大收益，短途物流企业则需根据铁路运输企业所制定的定价策略调整接驳运输费率，以提升自身收益.

(3)货运距离会对托运人运输方式的选择产生影响.货运距离在200 km以下时，铁路运输不具备运输优势，公路运输优势明显；货运距离在200～700 km范围时，铁路运输收益随着运输距离的增长而逐渐上升；货运距离在700 km以上时，铁路集装箱运输优势凸显，铁路企业可采用最小运行基价作为定价策略.