面向多用户类的拥堵和排放收费方案研究

席好宁，张 一，何 流，张 毅*，3

(1.清华大学清华—伯克利深圳学院，广东深圳518055；2.深圳市城市交通规划设计研究中心，广东深圳518057；3.清华大学自动化系，北京100084)

0 引 言

交通拥堵是各大城市普遍面临的社会问题.交通拥堵致使机动车加减速次数和怠速行驶状态不断增加，最终导致机动车尾气排放的增多.随着机动车保有量的迅速增加，机动车的尾气排放已经成为城市大气污染的主要来源.根据美国调查报告，机动车排放的HC占30%～50%，NOx占40%～60%，CO占80%～90%，我国调查报告显示80%以上的CO均源于机动车尾气排放[1]，因此本文选择CO的排放量作为排放的研究指标.

面向多用户类的道路拥堵收费研究可以分为两类：具有不同时间价值的用户(多时间价值用户)和拥有不同车型的用户(多车型用户).Leurent[2]，Marcotte[3]和 Mayet等[4]，Nagurney[5]等最早研究了多时间价值用户的均衡条件和系统总成本最优的问题.Dial[6]，Yang等[7]进一步证明了存在面向不同时间价值用户的匿名道路收费方案.Yang等[8]研究了基于系统总成本和系统总时间的双目标问题，并证明非负的路段拥堵收费方案可以使系统总成本实现最优；Guo等[9]进一步研究上述双目标问题，并证明非负的道路收费方案可以使帕累托有效流达到用户均衡状态.现有的面向多用户类的研究中，大部分以系统总成本和系统总时间为准则，很少以系统总时间和系统总排放为准则.Szeto等[10]通过仿真实验说明实施拥堵收费可能会造成排放增加，Nagurney A.[11]证明缓解拥堵和减少排放这两个目标有时无法同时实现.

不同车型具有不同的平均速度和排放量，因此欧洲国家分别针对大型客车、小型商用汽车、大型货车、公交车和小轿车等具有不同排放指标的车辆制定了不同的收费标准.针对不同车型收取不同的费用是一项长期行之有效的道路收费策略.Kawakami[12]最早提出基于车型的出行时间函数，Toint[13]和Marcotte[14]进一步研究了多车型用户的交通分配问题.Chen等[15]基于不同排放函数研究了基于道路收费方案使用户的帕累托有效流达到用户均衡状态的充分必要条件，但该研究未考虑多用户类因素.本文面向多时间价值用户和多车型的用户，研究是否存在有效的道路收费方案，以达到同时缓解拥堵和减少排放的目标.

1 符号与概念定义

1.1 符号定义

本文符号及其定义如表1所示.

表1 变量定义Table 1 Variable definition

1.2 帕累托有效流

本文通过式(1)描述的双目标优化问题来解释帕累托有效流.

显然，任何流量集合v对应的系统总排放E(v)和系统总出行时间T(v)不可能同时比帕累托最优流v*对应的系统总排放E(v*)和系统总出行时间T(v*)小，则流量集合v*∈Ωv被定义为帕累托有效流[15].分别以系统总出行时间最小(SO)和系统总排放最小(ME)为目标的两个解集恰好是帕累托前端的两个端点A和B，如图1所示.

2 服务于多时间价值用户的道路收费方案

2.1 多时间价值用户收费模型的条件

基于以下假设与条件研究多时间价值用户的收费方案.

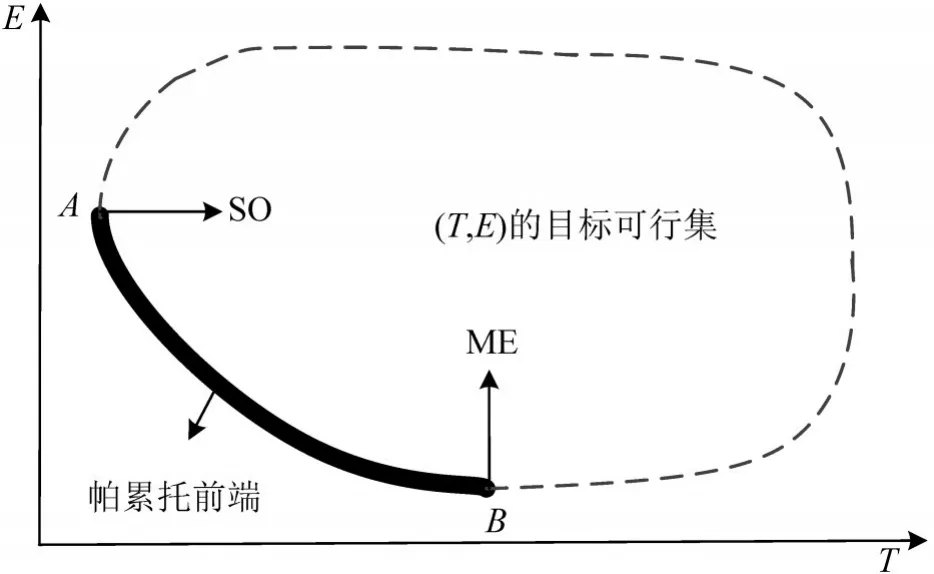
图1 双目标问题的帕累托前端Fig.1 Pareto frontier of bi-objective problem

假设OD对w∈W间第m类用户的出行量是固定的，路段出行时间函数和排放函数仅与该路段流量相关，与其他路段流量无关；CO的排放函数为凸函数，且随路段流量单调递增[9].

路段a上所有用户的路段流量集合用Φv表示为

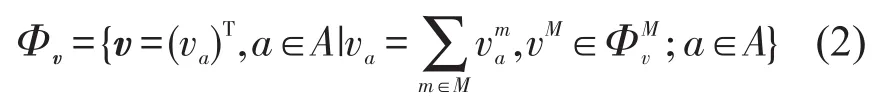
如果没有实施道路收费方案τa，第m类用户的成本为；如果实施收费方案τa，第m类用户的时间成本为.

如果第m类用户在OD对w之间选择路径r，则该用户在路径r上的费用成本为

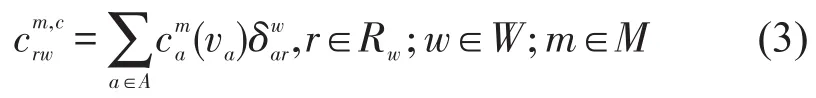
2.2 多时间价值用户的均衡条件

多时间用户分别基于时间成本准则和费用成本准则选择路径的均衡条件如下.

(1)多时间价值用户基于时间成本准则选择路径的均衡条件为

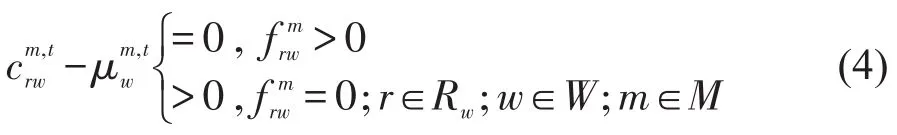
(2)多时间价值用户基于费用成本准则选择路径的均衡条件为

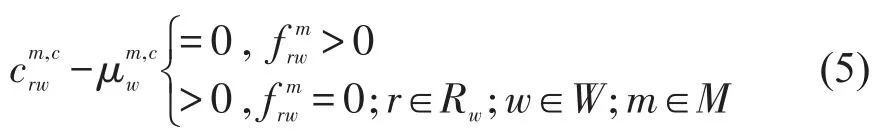
式(6)代表对多用户类实施匿名道路收费方案τa后的用户均衡问题的目标函数.

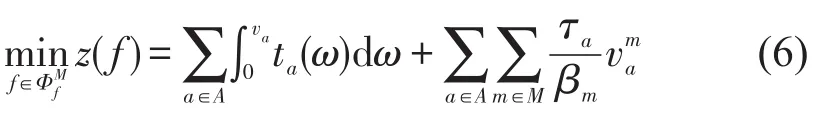
目标函数式(6)是关于路段a上所有用户的流量va单调递增的凸函数，va的值是唯一的，但不同时间价值用户的流量是不唯一的.同时，Guo等已经证明对同一路段上的多时间价值用户实施匿名收费可以得到唯一的系统总出行时间T和系统总成本C[9].

2.3 多时间价值用户均衡状态的实现

基于面向多时间价值用户的道路收费方案，本文分别考虑两个双目标优化问题，第1个双目标优化问题以系统总出行时间和系统总排放为优化目标，即

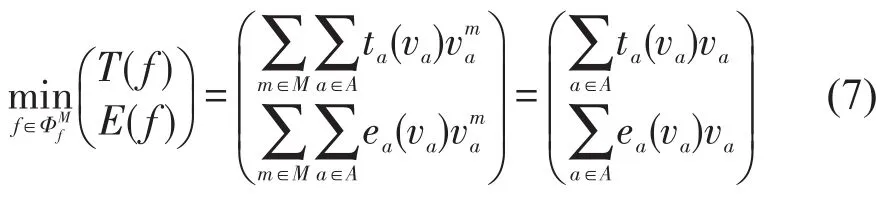
第2个双目标优化问题以系统总成本和系统总排放为优化目标，即

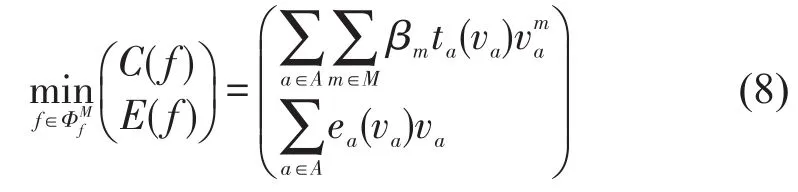
定理1对多时间价值用户而言，任意帕累托有效流都可以通过实施非负的匿名道路收费方案τa(a∈A)达到多用户类均衡状态.

证明设是路段出行时间函数，考虑下列LP问题：

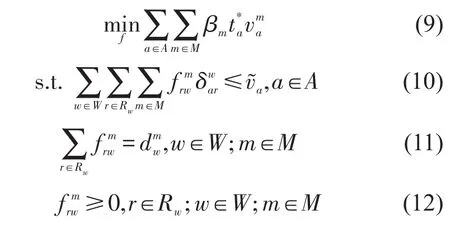
其对偶问题可以表示为

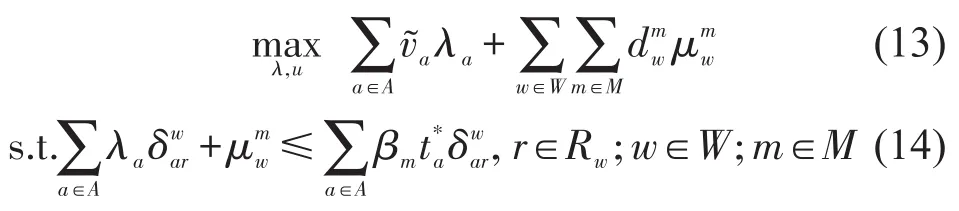
在原始问题和对偶问题的最优解处，根据互补松弛条件可以得到

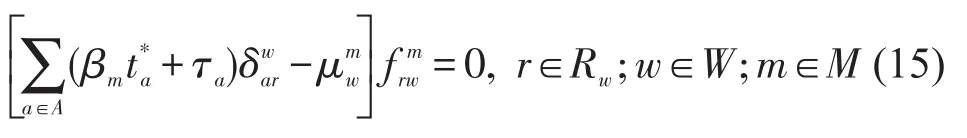
Yang等[8]已经证明等式(15)可等效为多用户类均衡条件式(5)，即通过匿名收费方案τa可以使多时间用户达到均衡状态.下面分别证明双目标优化问题式(7)对应的帕累托流和双目标优化问题式(8)对应的帕累托流是 LP 问题式(9)～式(12)的最优解.

假设v*不是该LP问题的最优解，是最优解，并且满足.由于是该LP问题的最优解，所以满 足，并且至少有一个b∈A满足；因为ea(va)单调递增，所以e,∀a∈A，结合上述条件可得到

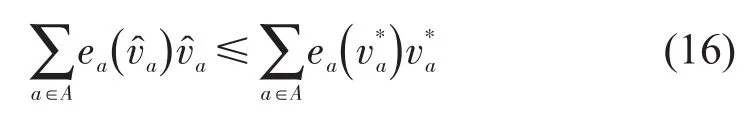
由于ta(va)单调递增，所以，并且至少有一个b∈A满足，结合上述条件可得到

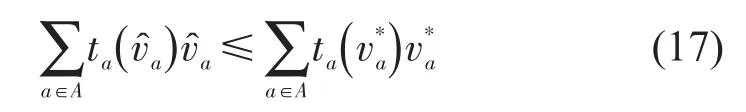
同理，假设不是该LP问题的最优解，是最优解，并且有.由于是该LP 问题的最优解，所以满足,∀a∈A，并且至少有一个b∈A满足，因为ea(va)单调递增,∀a∈A，结合上述条件可得到

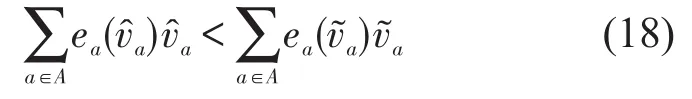
因为ta(va)单调递增，，，考虑不同类型用 户的时间价值βm(m∈M)，并对所有多用户类求和可以得到

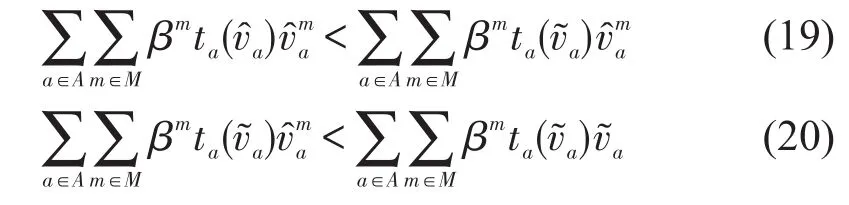
合并不等式(19)和式(20)可以得到

不等式(18)和式(21)与双目标优化问题式(8)中帕累托有效流的定义矛盾，因此原命题假设不成立，说明是LP问题的最优解.基于上述证明过程可以得到定理1.

进一步，同时考虑系统总出行时间、系统总成本和系统总排放的多目标优化问题的目标函数可表述为

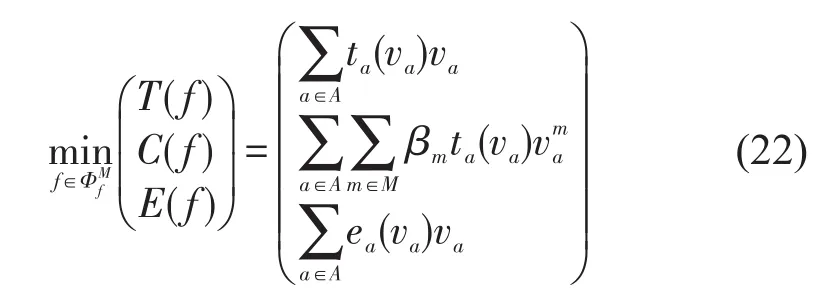
多目标问题式(22)的解集构成一个三维的平面，如图2所示.曲面上的每个点都代表一个帕累托有效解.同理可以证明出满足多目标优化问题式(22)的帕累托有效流也可以通过实施非负的路段收费τa达到多用户类均衡状态.

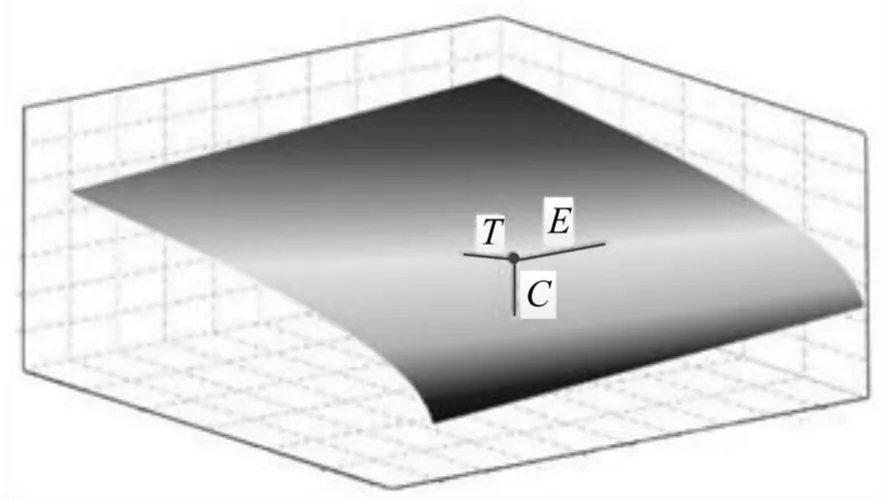
图2 多目标优化问题的帕累托最优平面Fig.2 Pareto optimal surface of multi-objective problem

3 服务于多车型用户的道路收费方案

对多时间价值用户而言，用户的出行时间函数和排放函数仅与该路段的流量相关，与其他路段的流量无关.然而对多车型用户而言，一方面需要考虑同一路段上不同车型间的相互影响，例如小轿车的增加可能轻微改变在某条道路上运行车辆的平均速度，但大货车的增加会严重影响该路段上运行车辆的平均速度；另一方面需要考虑在双向道路、或在没有信号灯的交叉路口等交通场景下，不同路段间的流量会互相影响.本文考虑路段流量间的互相影响，建立通用的模型来研究多车型用户的道路收费方案.

3.1 多车型用户收费模型的条件

基于以下假设与条件研究多车型用户的收费方案.

假设任意OD对w∈W间p车型用户的出行量是固定的；路段出行时间函数关于任意路段上的任意车型的用户流量都单调递增，q∈P,b∈A,p∈P,a∈A；路段排放函数为凸函数，且关于任意路段上任意车型的流量都单调递增；假设多车型用户的时间价值相同.

假设v代表多车型用户流量的集合，.基于多车型用户的路段出行时间函数的向量为对应的雅可比矩阵是(|A||P|)×(|A||P|)维的方阵，m=|P|,n=|A|,p1,p2,…,pm∈P,a1,a2,…,an∈A.是路段a上不同车型的排放函数，

3.2 多车型用户的均衡条件

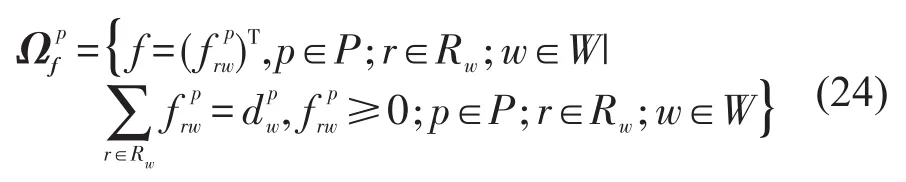
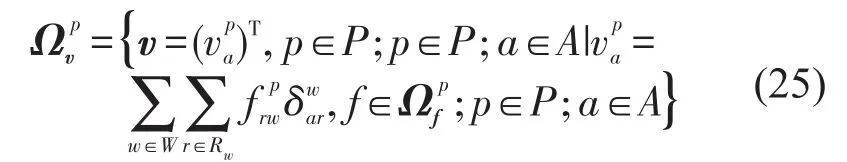
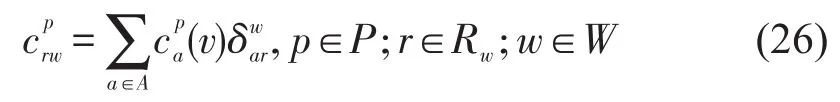
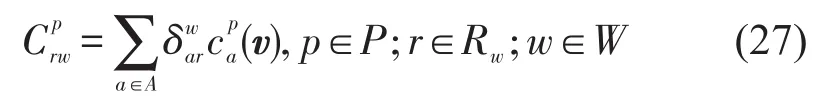
考虑不同路段间流量相互影响的多用户类均衡问题旨在找到路径流量和OD对间的成本向量，使得每一类车型的用户p∈P,w∈W,r∈Rw，都满足多车型用户均衡条件式(28).

当路段流量间的相互影响不对称时，无法通过求解数学规划问题得到用户均衡状态下的路段流量集合，因此使用变分不等式表示多车型用户的均衡条件.于是可有如下定理：

定理2对多车型用户而言，只要路段流量集合满足变分不等式(29)，就可以达到多用户类均衡状态.

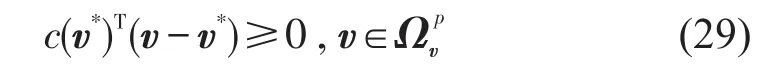
证明如果，由多车型用户均衡条件式(28)可知，.如果，由于，可以得到.由于，说明所有f*∈Ωfp都满足不等式(30).

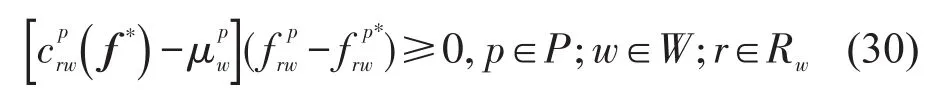
对每OD对w，每条路径r和每种车型p的流量求和可以得到

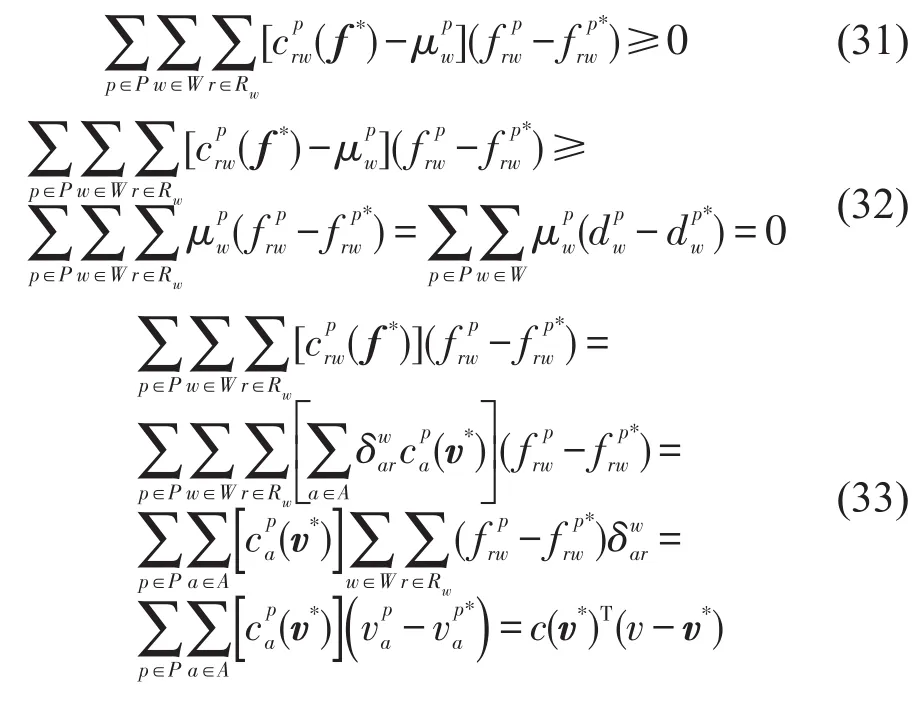
下面证明变分不等式(29)的解满足多车型用户的均衡条件式(28).由变分不等式(29)和等式(33)可以得到

不等式表示为

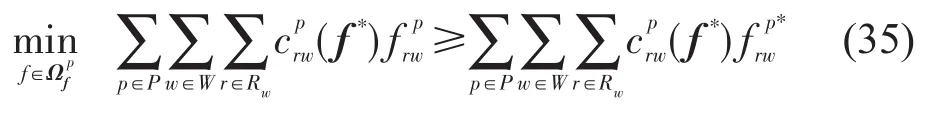
由于不等式(35)的右侧是一个常量，左侧是一个LP问题，f*是LP问题的最优解，式(36)～式(39)是该LP问题的KKT条件.

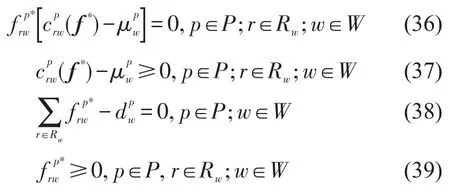
由于c(v)是连续函数，所以变分不等式(29)总是有解，下面给出其唯一解存在的定理.

定理3如果多车型用户的路段成本函数c(v)严格单调递增，即满足式(40)，那么变分不等式(29)存在唯一解，即存在唯一的路段流量集合.

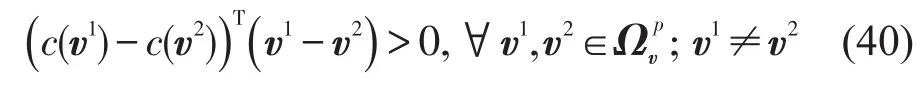
证明假设v1,v2是两个状态下的多车型用户均衡流，分别代入变分不等式(29)可得

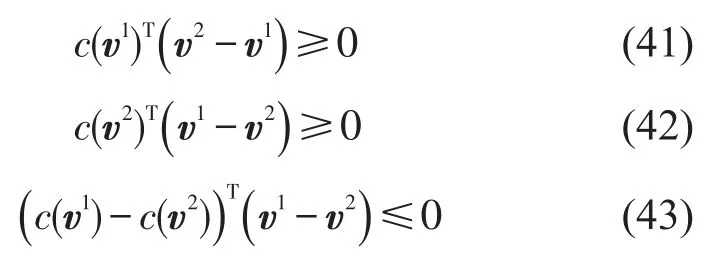
因为c(v)严格单调递增，所以v1=v2.

3.3 多车型用户均衡状态的实现

面向多车型用户的系统总出行时间和系统总排放的双目标优化问题表示为

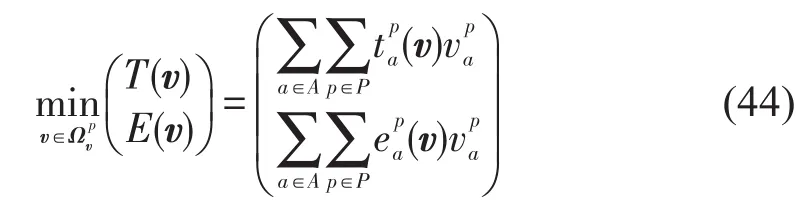
定理4对多车型用户而言，任意帕累托有效流可以通过实施非负的道路收费方案达到唯一的多用户类均衡状态.

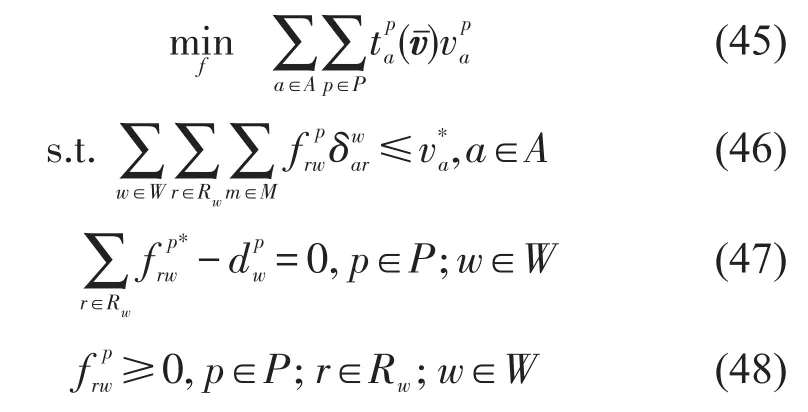
在原问题和对偶问题的最优值处，根据互补松弛条件得到

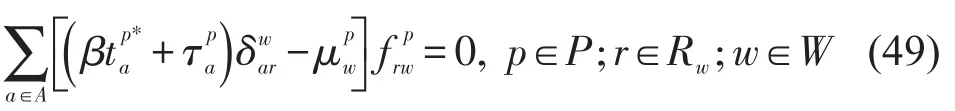
Yang等[8]已经证明不等式(49)可以等效为多时间价值用户均衡条件式(28)，即通过收费方案可使多车型用户达到均衡状态.下面用类似的方法证明满足双目标优化问题式(44)对应的帕累托有效流是LP问题的最优解.

由于不等式(50)和式(51)与双目标优化问题式(44)对应的帕累托有效流的定义矛盾，所以假设不成立，是LP问题的最优解.上述证明说明实施非负的收费方案可使多车型用户的帕累托有效流达到用户均衡状态.因为t(v)严格单调递增，由定理3可知，用户均衡状态下的流量集合是唯一的，因此得到定理4.

4 算例说明

考虑只有一个OD对的简单路网，OD对间有两条平行路段a和b，如图3所示，第m类用户和第n类用户的出行量相等：dm=dn=4，单位出行量为1 000 veh/h，时间价值分别为βm=1.0，βn=2.0.为便于说明多车型用户，假设所有大货车都在路段1上行驶，路段时间函数为t1=2v1+6；假设所有小轿车都在路段2上行驶，路段出行时间函数为t2=v2+8，路段排放函数为e(va)=0.2∙ta(va)∙ exp(1/ta(va)).

图3 算例示意图Fig.3 Example diagram

任选一个同时满足双目标问题式(8)和式(44)的帕累托有效流.

实施非负的路段收费方案τa后，如果第m类用户和第n类用户在费用决策准则下选择出行路径，从而实现用户均衡的状态，则系统的总成本C表示为

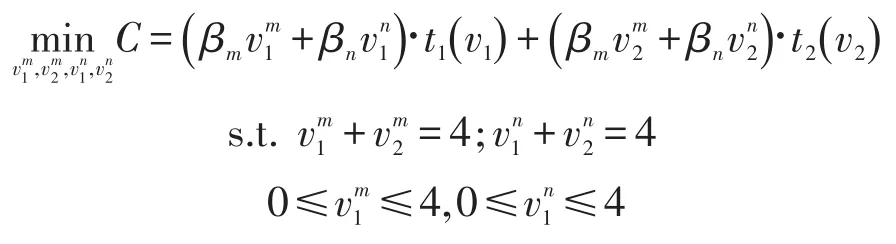
第m类用户在路段1上的流量，第n类用户在路段1上的流量和系统总成本C的关系如图4所示，实施收费方案(τ1,τ2)后达成的用户均衡流为，由图5可知，此时对应的系统总成本C=149.3，系统总排放E=2 136.

定理1和定理4说明通过实施非负的道路收费方案可使帕累托有效流达到用户均衡状态，根据用户均衡条件可以得到

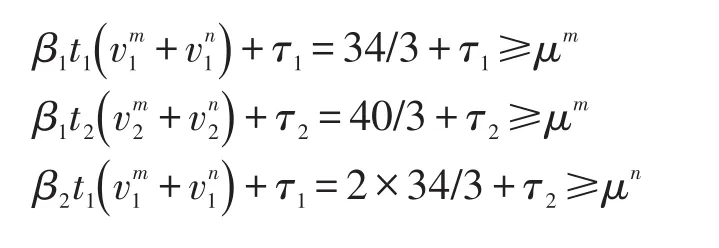
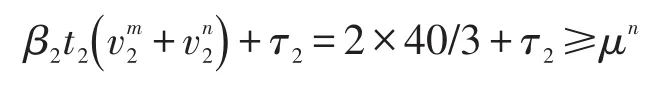
进一步简化路段收费集合的关系得到

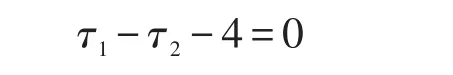
式中：μm和μn分别代表OD对间第m类用户和第n类用户的最小成本；τ1和τ2分别代表路段1和路段2的道路收费.

该算例说明通过对多时间价值用户和多车型用户实施相应的道路收费方案(τ1,τ2)，可以使任意帕累托有效流都达到多用户类均衡状态.

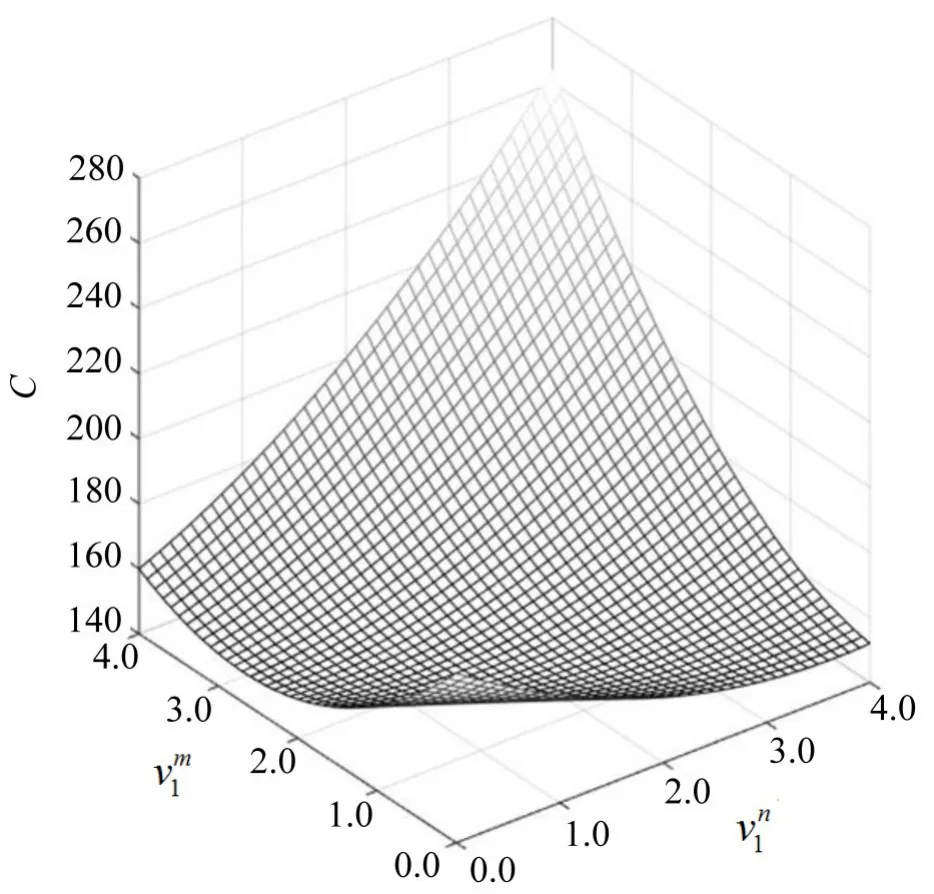
图4 目标函数的曲线图Fig.4 Curve surface graph of the objective function

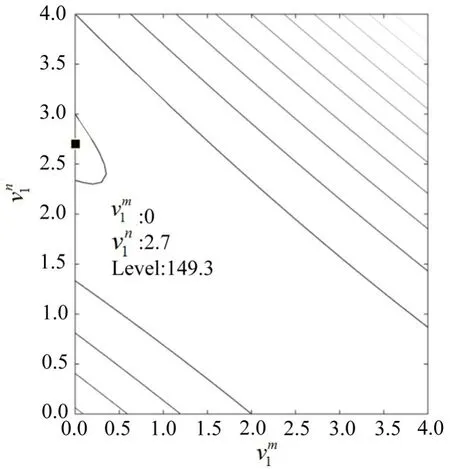
图5 目标函数的等值线Fig.5 Contours of the objective function

5 结论

本文首先面向多时间价值用户，分别建立了基于系统总排放和系统总出行时间与系统总排放和系统总出行成本的双目标优化模型，并证明任意帕累托有效流都可以通过非负的匿名道路收费方案达到多用户类均衡状态.然后面向有路段流量交互的多车型用户，分别给出使任意流量达到多用户类均衡状态和路段流量集合唯一的充分条件，并证明任意帕累托有效流都可以通过非负的道路收费方案达到均衡状态.最后通过算例验证了上述定理的合理有效性.