不是“押宝”，而是“构造”*——浅析2018全国Ⅰ(文)第17题的考生应答及教学思考

江西省九江市第七中学 (332000)

张明星

今年6月，笔者参加了2018年普通高等学校招生全国统一考试的监考工作，随后作为阅卷教师，又参加了文科数学全国Ⅰ卷第17题的改卷工作.回顾考场上考生的表现与试卷上考生的作答，现谈几点针对本题考生暴露出的问题及教学应对策略.

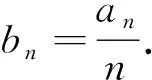
(1)求b1，b2，b3;

(2)判断数列{bn}是否为等比数列，并说明理由；

(3)求{an}的通项公式.

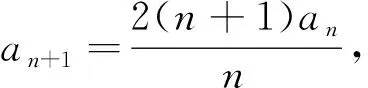
这一问主要考查数列递推公式的应用，逻辑上由a1⟹a2⟹a3，再由a1⟹b1，由a2⟹b2，由a3⟹b3.从考卷上考生的答题过程可以看到，本题的答题区域内，第(1)问实际空白的，寥寥无几，说明考生大多都掌握了“由数列的递推公式结合首项，依次递推出后一项”的方法，而数列{bn}与{an}的关系又比较明显，易得第(1)问答案.这一问主要的作答错误在于少数考生计算出错；也有极少数考生不能理解“nan+1=2(n+1)an”这个递推公式的意义，从而无从动笔.

针对第(1)问考生的作答表现，我认为在解答题第一道题，设计难度系数较低的第(1)问，有利于考生静下心来开始解答题的作答，这一问的设计，使得整道题呈现出合理的难度梯度，考查了数列的递推公式，结合后面两问，使得考查数列的知识点覆盖面更广；从考生丢分的情况分析，在平时的教学中，“逐个将n赋值代入到递推公式中，从而求得数列中的前几项”，是“求数列中的指定项，特别是数列前几项值”的重要方法，能够培养学生的“逻辑推理”、“运算能力”的核心素养，我们在教学时，不能因为“简单”而忽视，尤其要让学生体会“数列递推公式的涵义与作用”.

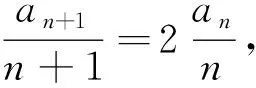
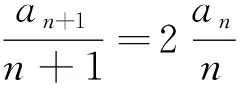
值得注意的是，第(2)问有考生在判断{bn}是否为等比数列之前，还作了{an}是否为特殊数列的判断；“由第(1)问中求出的a1=1，a2=4，a3=12，得出{an}为等差或等比这样的谬误”，想由{an}的“特殊性”得出{an}乃至{bn}的通项；也有考生写到“由b1=1，b2=2，b3=4，就匆忙下结论说“{bn}为等比数列甚至有说是等差数列”.这两类错误不是个例，必须引起我们警觉：有些同学在学习完《数列》章节之后，形成了“一个数列不是等差数列，就是等比数列”的思维定势，因此当他们在做本道题时，就像在“等差”与“等比”之间“押宝”，哪怕得到的结论牵强甚至是错误，也无力纠正.因此如何在平时的《数列》教学中让学生形成“辨证思维”的数学思想，而不是简单的“非此即彼”的狭隘思维模式，任重道远.但至少我们可以跟学生说清楚：并不是所有的数列都那么地“有规律”，例如：将周一集会升旗时，队伍中某一列学生的视力值排成一列，构成一个数列，该数列很可能既不等差，也不等比，“有规律”的数列是我们研究的一个重点，但不是我们研究的全部.

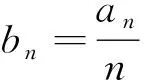
纵观本题的三个问题，显然第二问“判断数列{bn}是否为等比数列”，进而“根据等比数列的通项公式求出{bn}的通项”，是本道解答题的难点，平时我们讲到的可以构造出等比数列的情境有很多，重点是让学生明白构造的“新数列是否符合等比数列的定义(即从第二项起，后一项与前一项的比是否为一个与n无关的常数，或者用‘等比中项法’)”，大致按“观察、变形、下结论”这样的三部曲.

本道题数列{an}“不特殊”——既不是等差数列，也不是等比数列，但与{an}相关的另一个数列{bn}“特殊”(等比)，借助于这样一个“特殊”数列{bn}的通项公式，来求得这样一个“非特殊”数列{an}的通项，这就是第(3)问的解题思想.可以说“思想支配着我们的行动”，前面的“变形、构造等比数列”的方法、技巧，是在数学思想的支配下“动起来”的；只不过，在本题的“三问”设计之下，这种间接求得“非特殊”数列的难度降低了.