运用Matlab实现数值积分的教学研究

刘 冲

(安庆师范大学数学与计算科学学院，安徽安庆246133)

在很多积分问题中，古典的求解积分方法无论在理论上还是在解决实际问题中都起了很大的作用，但由于积分函数的复杂性，古典积分公式并不能完全解决定积分的计算问题。由此可见，通过原函数来计算积分有它的局限性。随着计算机和相应计算软件的飞速发展，积分数值计算方法[1-2]已成为很多应用专业的重要学习内容之一，也是数学和计算机等计算方向的大学本科生必学的内容。像Newton-Cotes公式、高斯公式、龙贝格公式是数值积分课程教学的重点，而方法原理及公式推导通常繁琐复杂，若结合图形和实例演示则能达到事半功倍的效果。对于图形计算演示，Matlab软件[3-4]具有很强的实用性，它能快捷处理数学计算问题，其强大的绘图功能和现成的数学计算函数库。在数值积分教学中有重要应用。

本文主要运用Matlab软件辅助数值积分解法原理、数值积分方法的教学，以达到更好的教学效果。

1 回归定义——机械求积

函数积分有很多常用的积分公式，但实际绝大数积分问题都不能用现成的积分公式精确求解，所以要寻求一些近似方法。这里根据积分思想，阐述积分公式计算的难点，由积分定义式引出数值积分思想，结合实例，运用Matlab推演简单的数值积分过程，这样学生很容易理解数值积分概念。

若一元函数f(x)在区间[a,b]上连续且其原函数为F(x)，可用Newton-Leibnitz公式

求定积分的值，而F(x)很难得到，这可回归到积分的原始定义：

其中N=(b-a)/Δx。由(1)式的极限形式可知，函数f(x)在区间[a,b]上的积分实际上可认为将区间化成无数小区间Δx，求函数f(x)覆盖每个小区间的矩形面积之和，则极限体现为区间足够小。从数值计算角度而言，极限可看成近似达到预期点的思想，即满足一定的精度要求，结果就认为到达极限。

根据(1)式，利用Matlab编程，对划分不同大小区间所得积分值如表1，并通过图形演示积分原理如图1～4。

由图1～4可知，当区间长度为0.02时，积分值基本上和原积分值相等，相应误差如表1所示。

表1 不同区间长度积分值比较（真实积分值为）

表1 不同区间长度积分值比较（真实积分值为）

项目数值积分值误差n=10 1.515 9 0.054 9 n=50 1.559 5 0.011 3 n=100 1.565 1 0.005 7 n=1 000 1.570 7 0.000 1

图2 10个区间积分覆盖面积

图3 50个区间积分覆盖面积

图4 100个区间积分覆盖面积

从表1可看出，当区间步长Δx足够小时，(1)式这种机械型积分基本上接近真实值，那是不是说只要区间步长Δx足够小，所有的积分通过(1)式都可近似计算出来？这显然不行，因为在实际问题中可能积分函数f(x)的数学形式不存在，仅知道几个测试点的函数值，或者积分函数很复杂，这样就很难用(1)式达到计算积分的目的，我们必须运用其他数值积分方法，其中插值型积分就是一个很好的方法。

2 对比分析——插值型积分

插值型积分是指用一近似函数φ(x)来代替原函数f(x)进行积分。在区间[a,b]上，近似函数φ(x)构造方法很多，不同的构造函数对应不同的积分方法。这里通过几类积分方法对比分析，让学生掌握插值型积分公式的构造原理，同时也帮助学生对插值理论知识进行巩固。

插值求积公式思想：设已知f(x)在区间[a,b]上对应的节点xi(i=0,1,…,n)有函数值f(xi)，构造n次拉格朗日插值多项式

分别利用上述4种方法对例1在区间[-1,2]进行求积，运用Matlab绘图演示每种方法构造思想，对比计算结果，分析计算误差。

图5为原积分覆盖面，图6为梯形公式方法的结果，利用插值方法构造一条近似直线代替函数曲线积分，用梯形覆盖面积作为原积分面积，很明显误差较大；图7为辛普森公式方法的结果是利用插值方法构造一条二次多项式函数代替函数积分，精度比线性的好，由于高次插值函数震荡的局限性，一般仅用低次插值函数近似；图8～10是将积分区间复化成很多小区间，然后再在每个小区间上利用梯形公式，可见细化区间也能达到提高精度的目的。龙贝格方法是根据图8和图9或图9和图10构造误差补偿，缩减复化区间数，从而减少计算量。几类方法相应误差如表2所示。

图5 原积分覆盖面

图6 梯形公式积分覆盖面

图7 辛普森公式积分覆盖面

图8 n=3复化梯形公式积分覆盖面

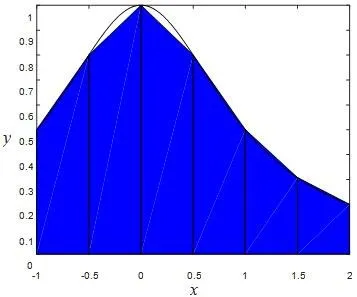
图9 n=6复化梯形公式积分覆盖面

图10 n=12复化梯形公式积分覆盖面

表2 不同方法积分值比较（真实值1.892 5）

通过实例，对比不同方法计算结果和误差，能让学生明白，梯形和辛普森公式计算简单，精度不高，复化形式梯形公式和龙贝格公式计算精度高，但计算量比较大，所以对于积分方法而言，没有绝对的好方法和差方法，只有针对具体问题谈论某些方法合不合适。

3 深入运用——差分变步长积分

从表2几种方法的对比结果可知，只要积分精度达到要求，方法的运用是越简单越好，但往往很多问题都需要高精度的计算结果，因此更多的时候需要进行积分方法改进。改进的方法通常体现在积分方法构造和积分步长的选取两方面。这里针对复杂的积分函数提出差分变步长的思想。

定义1 设函数f(x)在区间[a,b]上的等距节点为 xi∈[a,b],i=0,1,…,n，则函数f(x)在等距节点上的值为y0,y1,…,yn，称Δyi=yi-yi-1为函数f(x)在[xi-1,xi]上的差分。

定义2 函数f(x)在[xi-1,xi+1]上的差分为Δyi,Δyi+1，则称

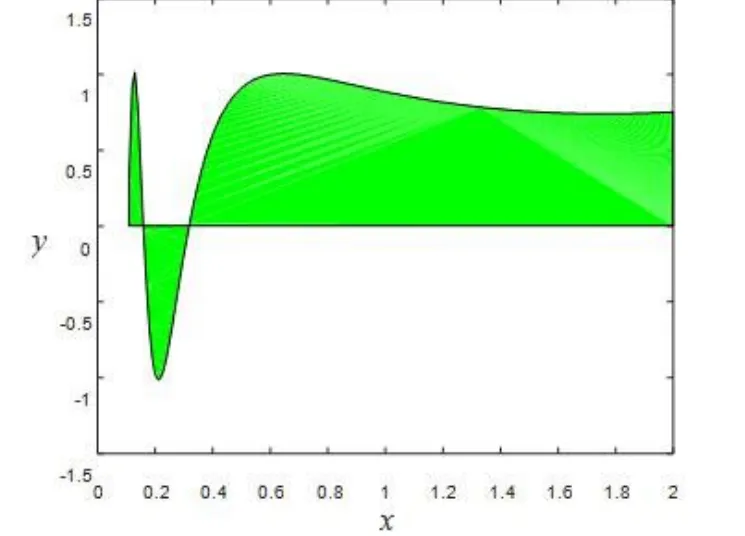
图11 原积分面积

为函数在区间[xi-1,xi+1]上的差分比。

根据函数f(x)在区间[a,b]上的差分比σi可知，若函数变化幅度不是很大，差分比σi近似为1；反之，差分比σi的绝对值远大于或小于1，则f(x)在区间[xi-1,xi+1]上积分需要进一步细化以获得高精度。下面以具体实例分析差分变步长积分方法。

通过Matlab绘图可知，积分函数在区间[0.11,0.3]上变化很大，采用10等分常规等距变步长的方法，误差较大，则通过计算区间[0.11,2]上相邻两小区间的差分比可知，在区间[0.11,0.389]上的差分比较大，因此可仅对区间[0.11,0.389]作进一步10倍细化即可。该方法对比文献[1-2]中出现的梯形公式、辛普森公式、复化梯形、龙贝格等方法面积覆盖图形如图11～16所示，几类方法计算结果和误差如表3表示。

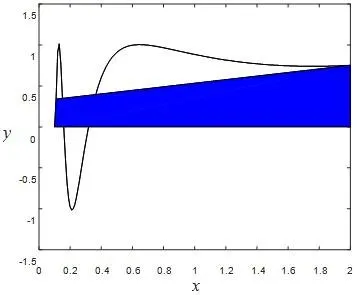
图12 梯形积分面积

图13 辛普森公式积分面积

图14 n=15复化梯形公式积分面积

图15 n=30复化梯形公式积分面积

图16 n=30差分变步长积分面积

表3 差分变步长方法与不同方法积分值比较（真实值1.297 5）

差分变步长方法主要是利用差分比的变化幅度来判断细化的区间，由图11～16可知，特别对于函数在区间变化幅度很大时，相同的计算量，差分变步长方法积分误差明显小很多。

4 结束语

本文主要应用Matlab软件编程计算和图像处理功能演示数值积分思想，运用实例对比分析不同插值积分方法的构造思路，并利用差分变步长的思想对积分方法作了进一步改进，使得知识点的讲解更加直观。通过图形直观地呈现解题原理，把Matlab软件处理数学问题强大能力和数学方法原理相结合，能让学生更容易理解积分概念，掌握数值积分方法的实现和运用，提高学生分析问题和解决问题的能力，更好地达到学以致用的目的。