两面多框可构视图的位置特征构形

张春艳，张顺利

(蚌埠学院机械与车辆工程学院，安徽蚌埠233030)

两面多框可构视图[1]智力构形的关键在于将多框视图分解或转化成子形体的视图，并确定子形体间的切割、叠加或综合方式及其交线特征。传统的形体分析法和线面分析法比较笼统，这导致在“二求三”智力构形实践中虽有充分的自由想象空间，但缺少系统的构形分析依据和设计方法。特征视图是视图中存在的一种客观现象[2]，一般最能清晰地表达形体上线面形状、性质和相对位置，且并非集中于同一视图。所以，当经过截切、叠加或综合方式生成组合体的形状特征视图和位置特征视图完整给出时，就确定了其表面的类属形状及其对投影面的相对位置。如果表达组合体表面的形状对投影面的相对位置特征，以及子形体之间的位置关系给得不齐全或视图选择不当，则组合体的结构形状具有可构性。因此，针对两面多框可构视图中存在的线框内接、线框包容和线框外接的图示特征与组合体叠加、切割关系的规律，在形体分析法和线面分析法的基础上，着眼于清晰易懂、操作性强的组合体构形思维方法更值得系统分析和归纳。

1 截切位置特征构形

1.1 截平面的性质构形

截平面相对投影面的位置确定了截交线或相贯线的投影特性，子图框可能对应虚体表面或截断面的实形、类似形或积聚投影。图1所示主、俯视图的外轮廓为矩形，即均由平线（与投影轴平行或垂直，下同）组成，主视图中的3个矩形子图框a'、b'、c'之间的交线均是侧垂线，与含有一虚线的俯视图对应，则各子图框的空间表面形状均为四边形且上下、左右位置特征确定，但前后表面性质不确定；平线1'（4'）2'（3'）对应矩形图框1234，表示水平面且为定形投影。因此，图框a'、b'、c'含有空间四边形的实形、类似形或积聚投影，如图1（a）含有两个水平面和一个正平面的截交线，图1（b）含有一个侧垂面和两个平行面（正平面和水平面）的截交线，图1（c）含有两个处于侧垂面的截交线，图1（d）含有3个侧垂面的截交线，图1（e）含有两个侧垂面和一个水平面的截交线。

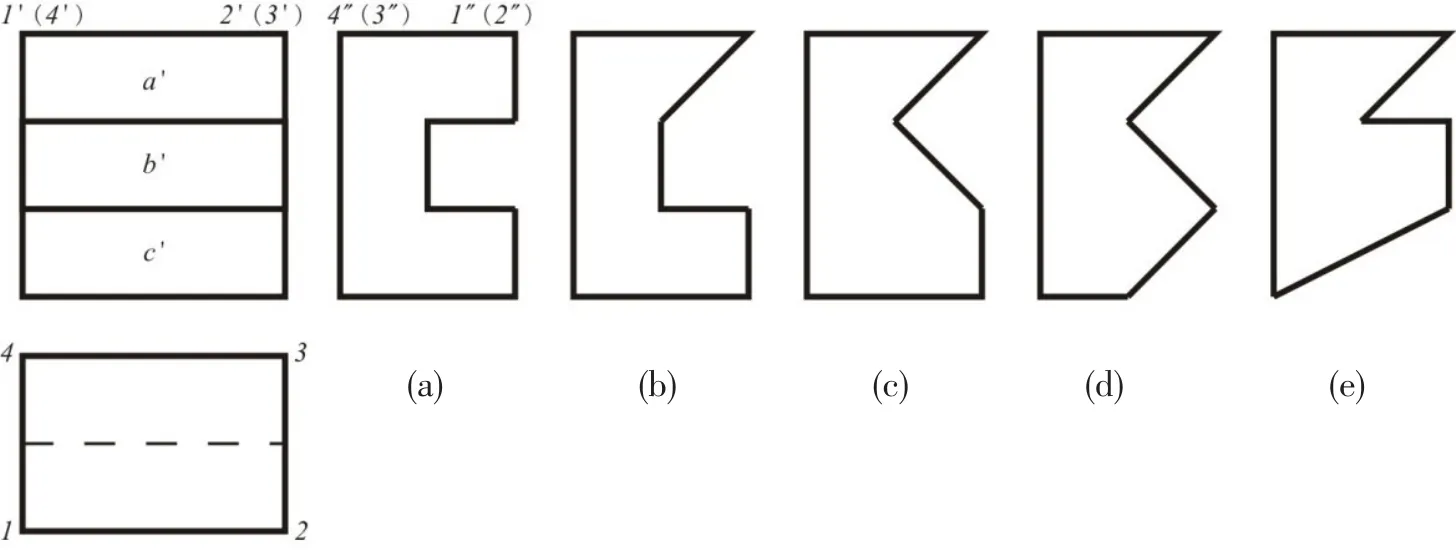
图1 截交线为平线对应截平面的性质构形

在两面多框纯矩形组合的空间构形中，当内图线与含有同面点集[3]的外图框分别垂直相交时，其空间构形一般先以同面点集对应的空间二维几何形状（投影面平行面）为一系列形状特征端面，再沿着该形状特征端面垂直的方向拉伸，可构造出不同结构形状的柱体。因此，图1的空间构形也可以将同面点集对应侧平面的二维多边形作为柱体的形状特征端面，即形状特征视图1（a）～（e），并沿着前后（宽度）方向拉伸该特征端面进行构形。

图2所示主、左视图[4]中的外轮廓为正方形，其空间最大公共点集域[5]为正方体；正方形的对角线即斜线可能是一般位置直线的类似形、投影面垂直面的积聚投影或投影面平行线的实形3种情况。若斜线作为一般位置直线的投影时，对应处于一个正垂面和一个侧垂面的截交线或处于一个正垂面和一个铅垂面的截交线，则该主、左视图是由两个处于垂直面的同类形[6]彼此互相补充构成的，如图2（a）和（c）；若斜线作为切割体表面上正平线和侧平线的投影时，对应两个处于一般位置的截交线（三角形），如图2（b）。

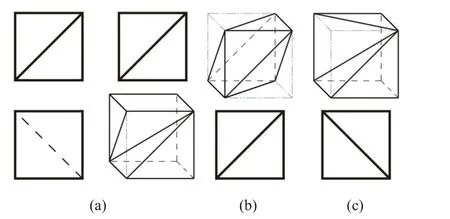
图2 截交线为斜线对应截平面的性质构形

1.2 截平面的个数构形

当给出子图框对应空间表面的实形、类似形、积聚投影及其组合时，就已经决定了多框视图中截平面或截交线的个数。图1（a）、（b）、（d）和（e）中分别含有3个截平面，图1（c）中则含有两个截交线。此外，重影和积聚在平面立体的截交线表达方面经常出现不定形多解。图3（a）～（f）在图2（a）、（c）的基础上主要通过新增1～2个截交线的重影所致；图3（g）在图2（b）的基础上大多是截交线兼有重影和积聚而产生的。可见，它们的共同点都是在同面点集范围内进行截交线中的端点和轮廓线构形，由于投影位置重合和积聚，产生了可构三视图[7]。

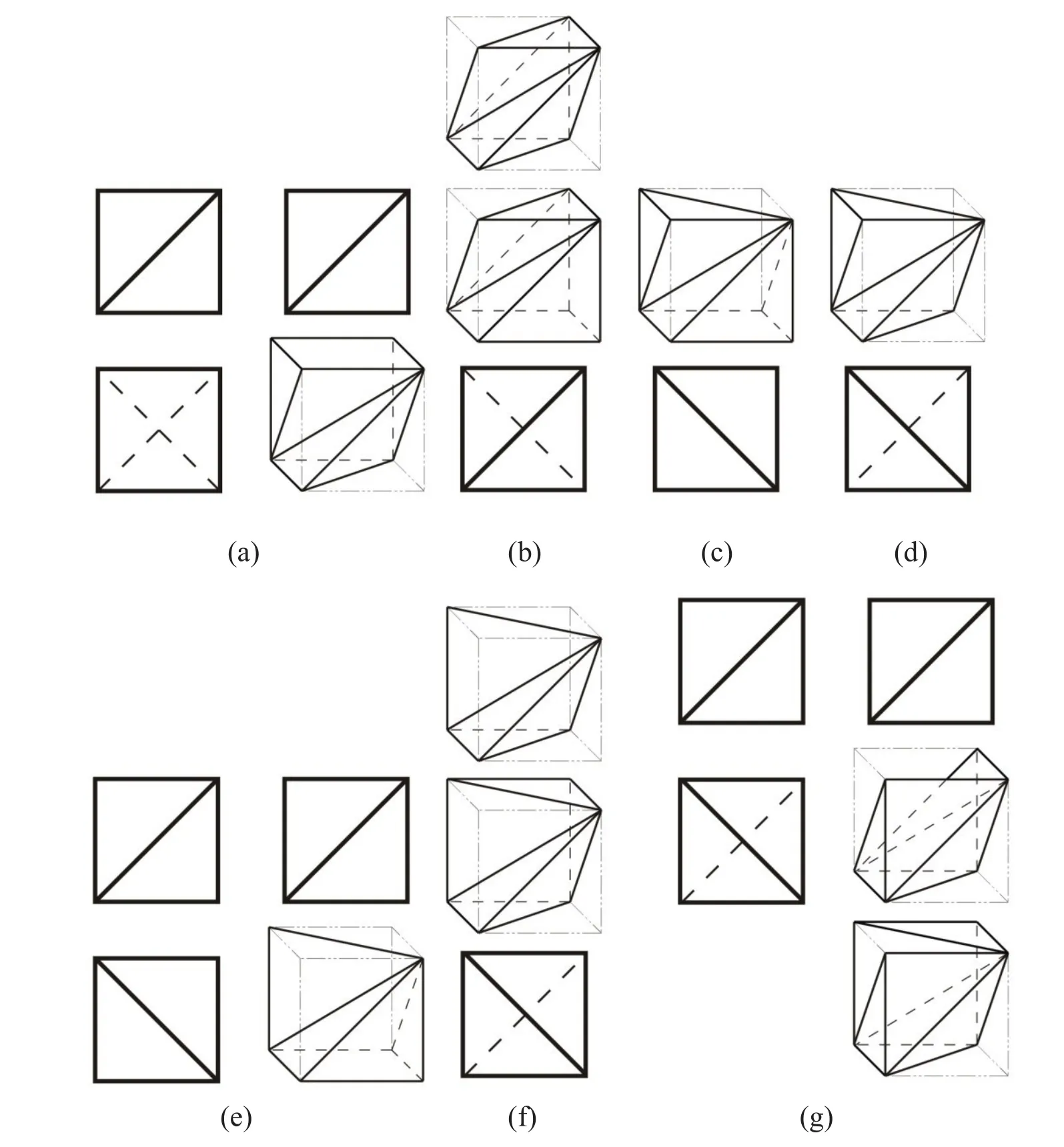
图3 截交线的重影和积聚构形

1.3 截切面的范围构形

截切面的范围构形即正斜、平曲、凹凸及其综合等方式变化，是在同面点集范围内截交线中的投影面平行线、垂直线进行凹、凸曲线变换，即针对截交线的空间平曲、凹凸形状特征进行构形，并在同面点集所在的实形视图中图示变换的汇交特征。直线过渡、尖点过渡和相切过渡是常见的3种汇交特征形式[8]。图1（a）截平面互相垂直相交为直线过渡，图1（c）～（d）、图2和图3中的截平面倾斜相交成为尖点过渡，图1（b）、（e）兼有直线过渡和尖点过渡。

图2中均含有两个截交线，在同面点集范围内存在投影面平行线且具有凹、凸曲线可构性，可形成尖点过渡，对应截交线由平面转换为曲面如图4（a）～（e）。其中，图2（a）和（c）中两个处于垂直投影面的截交线，但在同面点集范围内截交线中垂直线具有可逆性，只有平行线具有可构性；根据截交线的个数构形，可在同面点集范围内对其外表面进行曲面截切，可构造尖点过渡如图4（c）～（d），以及在尖点过渡范围内进行变量相切过渡如图4（e）。

图4 在同面点集范围内进行汇交特征构形

2 叠加位置特征构形

2.1 子形体间的空间位置构形

在保持已知题设条件不变的情况下，由给定形状的多个子形体及其表面按不同的相对位置组合在一起的构形，称为子形体间的空间位置构形。构形结果既反映子图框的形状和大小，又能组成一个整体，亦称为组合构形[9]。图1所示主、俯视图中的子图框在上下、前后方向上相邻并各自独立，左右齐平形成主、俯视图中的子图框间的关系为线框内接或外接，由于各图框对应明确，因此待构形的立体也可视为3个子形体的叠加体。

图5给出主、左视图的外轮廓为正方形，内部的3对平线分别与同面点集平行且垂直相交，对应有3个子形体。子形体的形状均可为长方体、三棱柱及其含有曲面或圆角的柱体中的一种或多种，其形状、位置组合变化丰富，部分组合体如图5（a）～（e）。其中，图5（a）、（b）和（c）均由同一组长方体、三棱柱和凹形柱体经过上、中、下位置的不同排列组合而成，均满足题设条件。

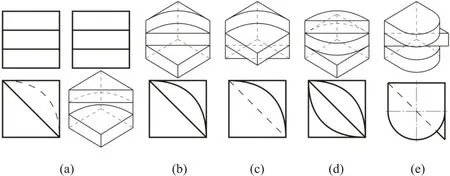
图5 子形体间的上、中、下位置组合构形

2.2 子形体本身的空间尺寸及其组合构形

子形体间的视图存在尺寸重合，引起的子形体本身的空间尺寸不确定及其组合间的位置、虚实关系具有可构性。图6所示主视图中的图框a'、b'、c'的形状特征视图确定，且与俯视图无类似形图框对应，必对应平线11、22、33，即3个封闭图框均表示正平面。由于图框a'、b'、c'左右长度相同，形体有前后宽度，因此面A、B、C前、中、后方向的尺寸位置就有多种可能性：（1）设图框c'在前且占前、中、后3层，图框b'居中且占中、后两层，图框a'在后且与图框b'、c'后平齐，如图6（a）；（2）在图6（a）的基础上，在后层切割去与图框c'形状相同的形体，即图框c'在前且占前、中两层，如图6（b）；（3）图框a'居中层，图框b'在前且占前、中两层，图框c'在后且占中、后两层，如图6（c）；（4）图框a'居中层，图框b'在前且占前、中、后3层，图框c'在后且占中、后两层，如图6（d）；（5）在图6（d）的基础上，在后层切割去与图框c'形状相同的形体，如图6（e）。兼顾图框b'、c'的左右两边线含有同面点集，对应侧平面的形状特征可构，其组合变化也就更多。

图6 子形体间在前、中、后方向的空间尺寸组合构形

3 综合截切、叠加位置特征构形

3.1 多重投影对应关系构形

当两个或多个子形体在某视图中的投影线共线时，它们的相对位置、虚实关系具有可构性。图7所示主视图中的图框a'、b'、c'与外图框之间形成相贯线，且与俯视图中的图框d、e投影线共线，其位置特征可构。圆形图框a'对应矩形图框，形状特征确定，但存在实圆柱和虚圆柱2种情况；若将图框b'、c'看作三棱柱、四棱柱的投影，其虚实位置组合的部分形体及其位置特征视图如图7（a）～（e）。再加上图框b'、c'的左右两边线含有同面点集，对应侧平面的形状特征可构，则在图框a'、b'、c'前后虚实位置组合变化的基础上，待构造立体的组合变化也就更加丰富。

图7 虚实位置组合变化及其位置特征视图

3.2 特征交线构形

特征交线是指子形体间的截交、相贯、相切等情况下的交线形状,用以反映子形体间的表面连接关系，及其子形体表面的结构形状。图7中的图框a'对应相贯线的形状特征完全确定，只有虚实关系具有可构性；图框b'、c'的形状特征交线在左视图，其形状特征和虚实关系均具有可构性。此外，当图框不易确定交线的性质时，可通过与相邻图框的交线进行判断[10]。图8所示主、左视图中的图框c'和c"成对应同类形且含有两对同面点集，应具有可构性，但根据可逆性图框的关联性却具有不可构性。三角形图框b'、b1'分别对应斜线b"、b1"，则面B、B1均为侧垂面具有可逆性；面C存在两条铅垂线且与面B、B1公用，则C框一定是铅垂平面，同时决定了与面A、A1的交线的性质与位置，它们的交线一定是铅垂平面，具有可逆性。因此，根据矩形图框a'、a"，a1'、a1"成对应同类形，以及视图外轮廓中含有同面点集对应的几何形状特征构形，可形成尖点过渡、相切过渡，如图8（a）～（e）。

图8 特征交线间的关联构形

4 位置特征的综合构形应用

图9所示主、俯视图的外轮廓为矩形，其空间最大点集域是长方体；内部各有5个子图框分别与外轮廓形成线框内接关系，反映了待构形的组合体一般为切割体。按照“上、中、下”和“后、中、前”的位置投影对应关系，可确定各子图框的投影对应关系及其可构性：一对同类形矩形图框d、d'，属于不定形；一对含有两个侧垂线的梯形图框e、e'，左右位置相同且方向相同，但e'框含有虚线，所以它们表示两个不同的面，即图框e、e'分别对应水平面（前）和侧垂面（后）；3对三角形图框：a、a',b、b',c、c'，均含有同面点集，具有可构性。在外轮廓对应空间最大点集域内，通过截切面的性质、个数的变化可得到图9（a）～（d）的部分平面切割体，形体整体和局部含有同面点集对应二维几何形状的凹凸变化后的部分切割体如图9（e）～（h）。

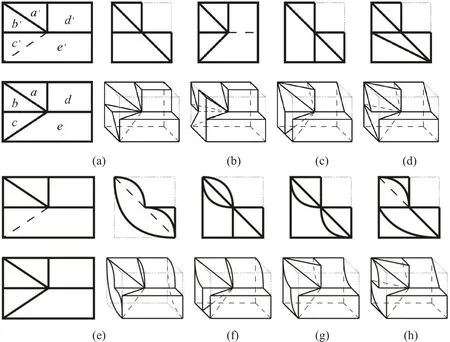
图9截切面的位置、个数和范围构形

图10 所示主、左视图[11]中，主视图中的4个图框 a'、b'、c'、d'在上下、左右方向上相邻并各自独立，形成线框外接，左视图中的3个图框a"、b"、e"为线框内接和包容，且子图框投影对应明确，则待构形的组合体为3个子形体按叠加方式而成的叠加体。主视图中的矩形图框c'、d'与左视图无类似形图框对应，必对应平线1"1"、2"2"，即两个封闭图框均为正平面，且具有可逆性；左视图中的多边形图框e"与平线3'3'对应，为侧平面亦具有可逆性；含有两对同面点集的同类形矩形图框a'、a"和梯形图框 b'、b"的形状特征和位置特征均具有可构性。因此，从平面立体的角度出发，3个子形体的组合情况为：图框a'、a"对应四棱台和三棱台（位置特征可构）；图框b'、b"对应四棱柱和三棱柱（位置特征可构）；图框e"与图框c'、d'共同组成“L”形棱柱体。按照上述子形体进行空间位置及其排列组合变化，构成的部分平面体如图10（a）～（i）。同理，在同面点集范围内改变截切面位置特征，可截切成一系列由平面和曲面组成的形体如图10（j）～（l）。

图10子形体间的叠加位置特征构形

图11 （a）[12]所示主视图中的4个子图框存在线框外接，俯视图中的5个子图框为线框外接且分别与外轮廓形成线框内接，则待构形的形体是以叠加方式为主的组合体。以分离面形状简单、数量最少,并且所获得的子形体数量最少为原则[13]，分离出2个子形体如图11（b）～（c），则它们的交线为图框d+e。

图11（b）中子图框间的关系为主视图线框外接，俯视图为线框外接和内接，可按切割或叠加方式形成立体。矩形图框a在主视图上没有对应的类似形，则对应平线2'2'，表达水平面A，位于b框的上方且具有可逆性；同理，图框d+e为水平面且具有可逆性；同类形梯形图框c'、c均可见、方向相同，且含有两条侧垂线，则面C为侧垂面且具有可逆性，斜线1'1'、2'2'对应一般位置直线或垂直面；图框b'、b含有一条侧垂线，且与面C公用斜线，因为面B、C不能共面，所以图框b'、b可能表达两个面（图框b'是正平面、图框b是正垂直面），或表达一个侧垂曲面。此外，图框b'、b的左边线和图框c、c'中的右边线，以及视图外轮廓中的左右边线含有同面点集。因此对应的平曲、凹凸变化得到的立体如图11（d）～（g）。图11（c）中矩形图框d'、d和e'、e的交线均与同面点集垂直相交，可看成切割体或叠加体，其空间构形应以同面点集对应的二维几何形状为特征端面并沿其垂直方向拉伸而成的柱体。综合上述两个子形体的结构形状可得出部分叠加体如图11（h）～（k）。

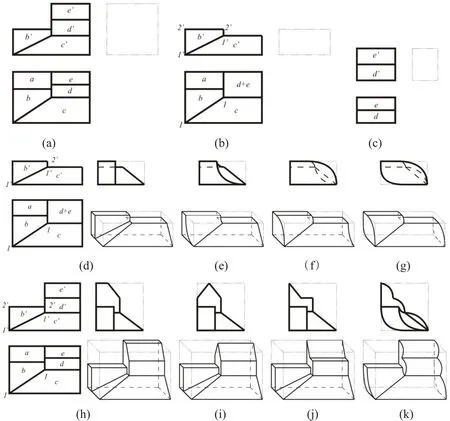
图11 综合截切和叠加位置特征构形

组合体是工业产品或工程形体的模型化[14]。因此，构成一个组合体所使用的子形体的形状、大小、构成方式、相对位置和虚实关系应尽可能多样、新颖、独特、完整，如图9（a）～（d）、图10（a）～（i）和图11（h）～（j）所示的构形方案均是由平面构成的，显得单调；图9（e）～（h）、图10（j）～（l）和图11（k）中含有两个及以上的曲面，结构形状较活泼。在此基础上应考虑强度、刚度、制造、装配以及经济性等问题，如图9（b）、（d）和（h）所示的结构形状较复杂，不易加工成型；图9（b）、图10（f）～（g）中的子形体I与子形体III、图10（h）中的子形体II与子形体III均含有线连接，不易构成一个整体；此外，图10（c）、（e）、（f）和（g）中子形体分布的情况，动感增强但平衡与稳定性较差。

5 结束语

综上所述，两面多框可构视图的位置特征构形是在同面点集范围内，“以位为主，形位结合”的思路，通过改变同面点集对应空间二维几何形状中轮廓线的位置特征和形状特征（不包括曲率变化以及轮廓线包围区的曲面），对应组合体表面的空间形状和位置变化来确定构形结果，构形结果包括平面体和含有曲面的形体，体现较高的发散度、变通度和新异度。

（1）截切位置特征构形是由于截切面与基本体共有点的位置、组成、个数和截切方式的变化而引起截交线的性质（位置）、个数、正斜、平曲、凹凸形状和汇交特征变化进行的结构形状构形。

（2）叠加位置特征构形主要是在子形体本身的结构形状、尺寸及其子形体间的位置、虚实变化时进行的，构形既反映子形体的结构形状和大小，又能表达整体的结构形状，以及子形体和整体之间的表面连接关系。

（3）当视图中存在多重投影对应时，子形体间的虚实关系具有可构性；当子形体间的交线形状为平面曲线或平面折线对应与投影轴平线时，截交线或相贯线的位置确定；根据图框具有的性质及其之间的关联性，可使含有同面点集的同类形图框可构自由度减少甚至具有可逆性。

对于两面多框可构视图中满足功能所需的结构形状、结构简单且紧凑、符合美学原理以及工艺要求等方面的综合构形设计将在后续项目中进一步探讨。