赋权分数布朗运动驱动的混合期权定价模型

杜姗姗,朱凤鸣,李芹影,王 浩,周芷薇

（蚌埠学院理学院，安徽 蚌埠 233030）

一、引言

有关期权定价问题的研究，Black-Scholes[1]于1973年在假设资产收益服从几何布朗运动的情形下，建立了欧式期权定价公式，二人也因此获得了1997年的诺贝尔经济学奖。在其后的四十年多年中，国内外的学者对其进行了深入的研究与推广。实证分析表明资本市场具有长程记忆性，因此一些学者使用具有长程相依性的分数布朗运动替代布朗运动改进经典的Black-Scholes期权定价模型，如文献[2]-[4]等。

作为分数布朗运动的扩张，Bojdecki等[5]首次建立并研究了一类更广泛的不具有平稳增量但具有分数布朗运动一些主要性质的自相似高斯过程，它来自于具有泊松初始条件的分支粒子的占位时，称为赋权分数布朗运动 (weighted fractional Brownian motion)。所谓赋权分数布朗运动是指协方差函数为

的中心化高斯过程，其中

a＞ -1,|b|＜ 1,|b|＜a+1。

当a＝0时，在相差一个常数倍数的意义下，赋权分数布朗运动退化为Hurs指数为的分数布朗运动。赋权分数布朗运动具有许多类似分数布朗运动的性质，如自相似性、轨道连续性、既不是马尔科夫过程又不是半鞅。更多此随机过程的知识请参考文献[6]-[7]。Sun Yan[8]首次研究了赋权分数布朗运动驱动的欧式期权定价公式，在上述文献的基础上，本文我们研究赋权分数布朗运动驱动的混合期权定价赋权分数布朗运动环境下的混合交换期权定价问题。在标的资产服从几何赋权分数布朗运动的情况下，利用保险精算的方法推导出了期权的定价公式。

本文的组织结构如下,第一部分给出了赋权分数布朗运动的定义及其驱动的期权定价公式模型；第二部分得出了混合交换期权定价公式；第三部分对本文进行总结。

二、赋权分数布朗运动驱动的期权定价模型

假设在金融市场存在着两种资产,一种是债券,另外一种是股票。假设债券在t时刻的无风险利率为 r；股票在 t时刻的价格设 S（t），且股票价格过程（t）满足

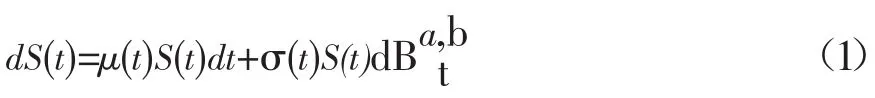
其中μ(t)表示期望收益率、σ(t)表示波动率和无风险利率表示赋权分数布朗运动。

现在考虑时间区间为[0,T2]，令{S(t):t≥0}表示完备概率空间(Ω,F,P)上的随机过程{Ft:t≥0},表示S(t)生成的σ-代数,而S(0)＝S是大于零的常数。

定义1 令t∈[0,T]，价格过程S(t)的期望收益率μ定义为，债券的价格P(t)满足方程d P（t）＝P(t)rdt，且 P(0)＝ 1,其中 r为 t时刻的瞬时利息率。

定义2 期权的保险精算定价等于股票到期日价格按期望收益率折现的现值与执行价(债券)按无风险利率折现的现值的差,在股票实际分布的概率测度下的数学期望值。

三、赋权分数布朗运动环境下的混合期权的保险精算定价

众所周知，混合期权是以期权为标的资产的期权,主要有以下4种:①买权的买权；②买权的卖权；③卖权的买权；④卖权的卖权.本文主要介绍①买权的买权,其它几种混合期权的公式读者可以类似推导。

买权的买权就是以买权为标的的买权,其到期时现金流量为：

CCT1＝max[0,C(S(T1),T1)-K]，

其中标的买权的标的资产S(t)表示基本标的资产t时的价格,t∈[0,T]；记标的买权的执行价格为K；标的买权的到期时为T2；标的买权在时的价格为C(S(t),t)；混合买权的执行价格为K(即买权的买权执行价格)；T1为混合买权的到期时0＜T1＜T2，即混合买权的到期时在标的买权的到期时之前).

定义3 当期权被执行时,混合期权的保险精算价值CC(S,0)为：

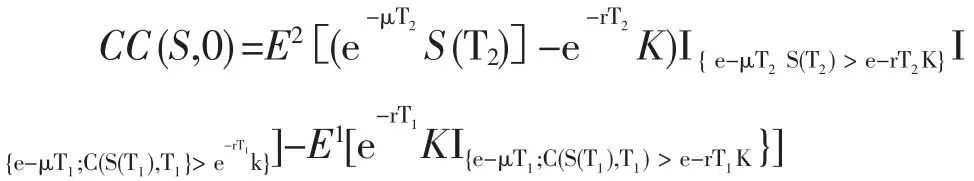
假设股票的价格过程{S(t):t≥0}满足方程(1),其中常数μ,σ分别表示股票价格的期望收益率和波动率,B a,b t 表示赋权分数布朗运动。

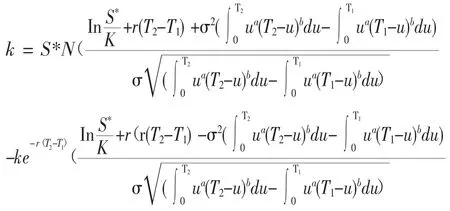
证明 由（1）式可知

定理1 假设{S(t):t≥0}满足方程(1)且风险资产在有效期内无红利支付,则

其中

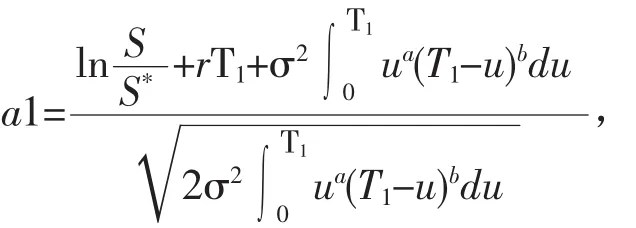
证明 因为

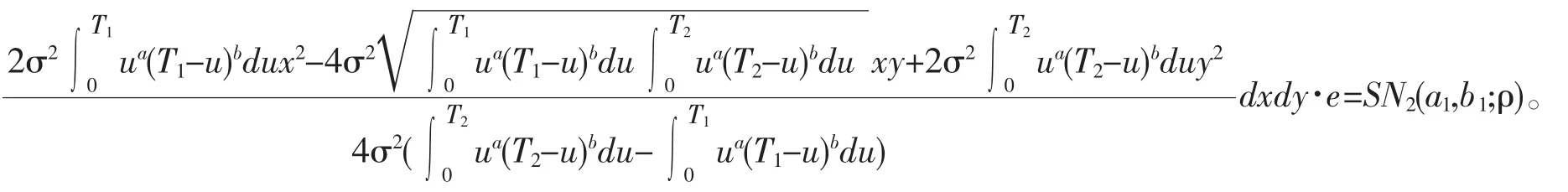
其中

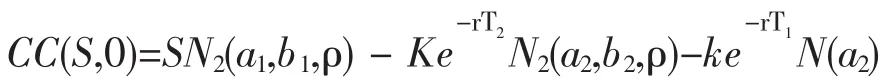
四、结论

本文利用保险精算的方程研究了赋权分数布朗运动符合的金融市场的交换期权定价问题，给出了期权定价公式。是对经典布朗运动及分数布朗运动驱动的金融模型的深入研究，为金融市场复合期权的定价提供了理论依据。未来我们将进一步研究赋权分数布朗运动驱动的亚式、美式等类型期权的定价问题。