积分因子在两类线性微分方程中的应用

杨 青

（正德职业技术学院，江苏 南京 211106）

一、引言

在常微分方程的学习过程中，教材基本上是根据不同的微分方程类型，分别给出了相应的通解的求法和步骤，比对不同的方法，可以看出积分在各种题型中的重要性。对比阅读了相关文献，尝试从积分因子入手，将待解微分方程降阶，巧解一些微分方程，并以此建立一些适用的公式帮助解题。

二、积分因子在一阶非齐次线性微分方程的应用

一阶非齐次线性微分方程的一般形式是：

高等数学教材中大多采用常数变易法，若p(x)作为连续函数是可积的，那么经过化简和计算就可以求出它的通解为：

分析给出的通解，使用了多次积分，同时考查了积分运算的技巧，从而增大了解题的难度，为了避免这一问题的出现。可以尝试引用积分因子进行化简，利用积分与微分互逆的关系，将导数的乘法和除法运算公式展开，从而发现引入了积分因子，不仅减少了积分的次数，还能保证解题的质量。

若存在非零可导函数f（x）和连续函数g（x），有

推论1.1若方程(2)中的连续函数g（x）＝f′（x），则一阶非齐次线性微分方程(3)的通解可以化简为

亦可换一种思路，假设同样存在非零可导函数f（x）和连续函数g（x），有

同理可得即

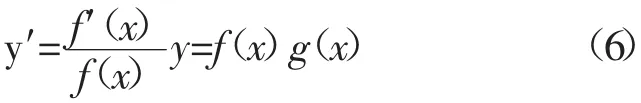
此时y′和y项的系数也分别满足f（x）和f′（x）的关系，由此便有以下结论。

推论2.1若方程(2)中的连续函数g（x）＝f′（x），则一阶非齐次线性微分方程(6)的通解可以化简为y＝f（x）［f（x）+C］

因此在解答一阶非齐次线性微分方程的过程中，只需根据方程(1)中的p（x），推导出f（x）的表达式，试算y′和y项的系数是否存在f（x）和f′（x）的关系，若满足，特别是遇到g（x）又可以化简成与f′（x）相关的形式，计算显然更加便捷。

解：将该微分方程化简为xy′+y＝ex

可以令f（x）＝x，且有f′（x）＝1，

解：将该微分方程化简为（cos x）y′+（-sin x）y＝sin x cos2x，可以令f（x）＝cos x，且有f′（x）＝-sin x，

代入通解公式y＝f（x）［f（x）+C］，

得通解y＝-cos2x+Ccos x

三、积分因子在二阶变系数非齐次线性微分方程中的应用

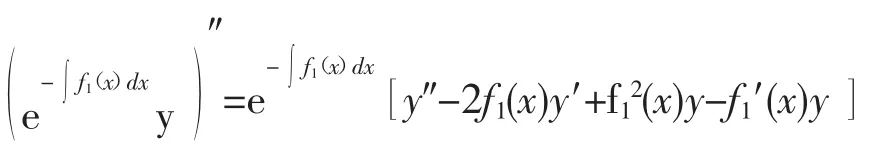
若有(8)和(9)相等，可以比较y′和y项的系数有

当二阶变系数非齐次线性微分方程中的p（x）和q（x）符合(10)的关系，便可以此微分方程简化，同时得

即

利用这种方法巧算二阶变系数非齐次线性微分方程，避免了计算通解时既要算相应的齐次方程的通解，又要算原微分方程的特解问题，而是直接利用积分因子将复杂的微分方程按照降阶思想进行计算，只需寻找合适的就可以解决一类微分方程的问题。

解：将该微分方程中 p（x）＝4x，q（x）＝4x2+2，满足（10），有f1（x）＝-2x，且有f1′（x）＝-2，

代入通解公式

四、结论

不少文献记载了积分因子的作用，在求解微分方程的过程中，显现出了优势。本文利用了导数的积和商的求导法则，进一步证明了积分因子的形式和作用。深入探讨积分因子在二阶变系数非齐次线性微分方程中的实用性，巧妙的绕开了求通解的繁琐计算过程，简化了解题的难度和复杂的程度，让学习者有信心解答问题。当然如果将积分因子引入更高阶的微分方程的运算也是可以的，只是在推导的过程中会更加繁杂，同时文中的推导思路还需要完善，扩大应用的范围，便于学习者更易掌握。