基于solidThinking Inspire的控制臂优化设计

张 涛

（华晨雷诺金杯汽车有限公司，辽宁 沈阳 110044）

前言

控制臂是具有导向和传力作用的悬架部件。其主要作用是将车轮上各方向的力传递给车身，同时还能保证车轮按一定轨迹运动。控制臂分别通过球铰和衬套把车轮和车身弹性地连接在一起。它的重量和性能参数对前悬架系统的整体表现有重要影响。

在汽车轻量化普遍受到主机厂重视趋势下，控制臂的减重工作也显得尤为重要。文章利用Altair公司的solidThinking Inspire软件[1]（以下称为solidThinking软件）在产品开发前期进行拓扑优化[2]，在满足强度性能要求的前提下，实现了结构的优化减重。

1 原始设计

图1所示为某车型控制臂的原始设计结构，该结构已充分考虑了控制臂与周边零件的空间位置关系，避免了装配过程和车辆行驶过程中与周边部件产生干涉。接下来所有在solidThinking软件中进行的优化工作都是基于这个几何模型。

图1 控制臂原始几何模型

2 优化流程

整体的优化设计思路如图2所示。

图2 优化流程

3 优化分析

3.1 定义设计空间

在开始进行优化设计前，首先定义结构的设计空间[3]，由于各安装孔是用来固定和安装控制臂的，需要保持位置和形状基本不变，所以将其定义为非设计空间，而将控制臂的本体部分定义为设计空间。

图3 定义设计空间

因为原始几何为一体模型，不能将控制臂本体和安装孔分别定义，所以在优化分析前通过solidThinking软件参照原始几何重新设计了新的安装孔，使其与控制臂本体互为独立但保持连接关系的几何结构，这一改动对整个结构的强度影响可以忽略不计。

分别完成定义之后，设计空间的区域显示为如图3所示的红棕色，非设计空间仍为灰色。

3.2 创建材料属性

选取控制臂材料为STEEL（AISI304），材料性能参数为，杨氏模量 E：1.95×105Mpa；泊松比 Nu：0.29；密度 ρ：8.0×10-9t/mm3；屈服极限 σs：215Mpa。

3.3 创建载荷工况

3.3.1 创建边界条件

根据控制臂在实车中的安装状态，对控制臂的副车架前安装点施加 X、Y、Z三个方向的约束，对控制臂的副车架后安装点施加Y、Z两个方向的约束（根据过往的分析经验，后安装点放开 X向约束，应力计算会更准确一些），而对控制臂的转向节安装点施加Z方向的约束。

3.3.2 创建工况载荷

控制臂的转向节安装点一般采用球销结构，所以只受力的作用，而不承受扭矩作用，另外因为施加了Z方向的约束，所以在该点只施加X、Y方向的力。在控制臂的副车架前安装点，因为约束了所有平动自由度，所以不加载力，只施加扭矩。而在控制臂的副车架后安装点，因为放开了X向约束，所以在该安装点，施加X向的作用力和扭矩。

根据控制臂在车辆实际行驶中的受力情况，选取了如表1所示六个比较典型的强度分析工况。

表1 强度分析工况描述

将六个工况的载荷和约束施加到模型后如图4所示。

图4 载荷和约束

3.4 设置形状控制

零部件拓扑优化后的结果在满足优化目标的前提下，有时候会出现现有工艺无法实现的结构，这样的结构对于后续的优化工作是没有意义的。因此，优化过程中有必要用到solidThinking软件的形状控制模块。

针对控制臂结构，选择了双向拔模。如图5所示，上下箭头代表拔模方向为双向。

图5 双向拔模形状控制

3.5 运行优化分析

3.5.1 运行优化分析

solidThinking软件提供了两种不同的优化目标，包括最小化质量（当以最小化质量为目标优化时，载荷幅值对于得到最准确的结果来说具有最关键性的作用。除了准确的载荷幅值，材料的选择也会起到重要作用。）和最大化刚度（当以最大化刚度为目标优化时，求解器并不注重各个安装点施加载荷的值，而会更加注重各个安装点载荷值之间的相对比例。）。

首先将最大化刚度作为优化目标，质量目标设为设计空间总体的30%，厚度约束设置为最小30mm，最大60mm，其余选项均为solidThinking软件默认值。

3.5.2 查看优化结果

设置完成后开始运行求解，当运行完成后，优化结果并不一定具有合理的结构。使用如图6所示形状探索器，拖动拓扑滑块找到最佳形状（以保证传力结构的完整性和整个结构的工艺性为原则）。

图6 形状探索器

通过调整拓扑滑块后，得到本次优化的结果如图7所示。

图7 最大化刚度—30%质量目标

3.5.3 调整优化目标

因为前文提到过，以刚度为目标进行优化时，软件并不注重载荷值，所以得到的较为单薄的优化结果对整个结构的应力控制并不会太好。

接下来将质量目标调整到40%，依旧调整拓扑滑块（后文中涉及到的优化结果都是通过调整拓扑滑块得到，后续不再赘述）得到优化结果如图8所示。

图8 最大化刚度—40%质量目标

继续上调质量目标到50%，优化结果如图9所示。

图9 最大化刚度—50%质量目标

接下来，再以最小化质量为目标进行优化，分别设置最小安全系数为1.8、1.5、1.2，得到优化结果如下图10～12所示。

图10 最小化质量—最小安全系数1.8

图11 最小化质量—最小 安全系数1.5

图12 最小化质量—最小安全系数1.2

结合原始结构和工艺性考虑，认为第三种和第六种拓扑结果是比较合理的优化方案。

3.5.4 优化结果几何重构

导出第六种拓扑几何模型，再基于该拓扑几何模型，在catia软件中对原始几何进行有目的性的开孔重构，得到新的控制臂的几何模型如图13所示：

图13 重构几何模型

4 优化结果验证

图14 垂直冲击工况

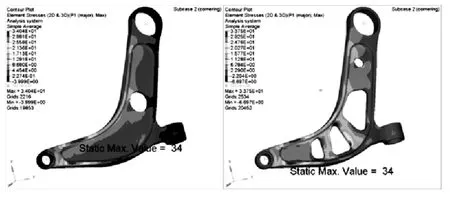
图15 转向工况

图16 后制动工况

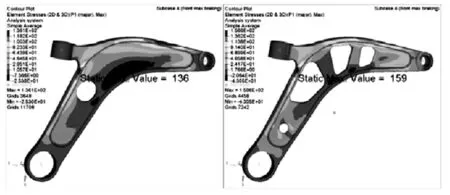
图17 最大制动工况

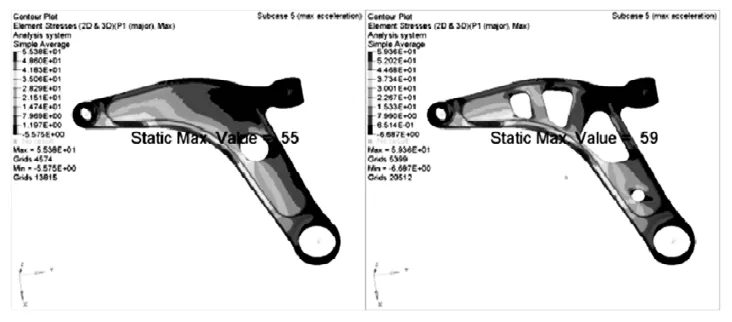
图18 最大加速工况

图19 侧碰工况

接下来通过Hyperworks软件进行加载计算，对比优化前后控制臂各工况的应力情况。左为原始结构，右为优化后结构。各工况最大应力值如图14～图19所示。

详细的最大应力数据对比如图 20所示。应力单位为Mpa。

图20 优化前后应力对比

优化后，各工况最大应力均有一定的增加，其中最大制动工况应力增加最多，应力值为159Mpa，仍小于材料的屈服极限215Mpa。一般情况下认为屈服极限即为许用应力[4]，但为确保留有一定的安全余量会用安全系数来控制许用应力的大小。而优化后最大制动工况仍有1.35的安全系数，因此从强度性能和安全系数角度考虑，优化的结果是满足需求的。

5 结论

通过solidThinking软件的优化分析，最终得到了控制臂的一种比较合理的材料分布状态。在保证零件力学性能的同时，控制臂的重量也从最初的7.64kg下降到6.52kg，减重比例达到 14.6%。减重优化效果明显，对设计部门有一定的参考价值。