车辆减振技术研究

陈俊杰，李菲，吕江毅，侯庆红

（1.北京电子科技职业学院，北京 100176；2.中国质量认证中心南京分中心，江苏 南京 210019）

前言

汽车行驶过程中，汽车会受到各种方面的振动激励。路面激励、动力传动系统、风激励、排气系统激励、轮胎振动等都是车辆上的主要振源。驾驶员在车辆内部的主观感受，是驾驶员和乘员对车辆振动的主观评价。载货汽车还包含货物在车辆上不得受损。车辆的减振能力不仅影响车辆的行驶舒适性，还会影响车辆的行驶安全性和操稳性。车辆减振能力是保证车辆具备良好的舒适和操纵性能[1]。

汽车平顺性是人车路汽车系统动力学研究的范畴。其中路面是激励环节，车辆可以简化为一个多自由度振动系统，人的主观感受感知的是系统的响应环节，系统组成框图如下。

图1 “人-车-路”系统组成框图

研究汽车行驶平顺性最重要的两个方面：1）车辆结构特性的研究；2）乘员对车体振动的主观感受的研究。第一部分属于对车的研究，通过优化振动能量传递路径，降低车辆在整个车速行驶范围内传递到乘员身体的振动能量。第二部分属于对人的研究，属于舒适性评价的问题。本文从理论、试验等多方面对车辆的减振方法进行研究，为技术人员提供参考。

1 车辆减振理论研究方法

多自由度振动模型的建立一直是汽车动力学领域中的重要研究课题，它是解决车辆振动问题非常好的数学工具[2]。根据车辆动力学仿真的研究目的，应该建立合适的数学模型。在计算机没有发明以前，通常建立二自由度或者三自由度模型，这只能对车身结构振动响应做定性分析。单自由度单轮模型只能反应下整车运动情况；三自由度单轮模型可以引入悬架参数和座椅参数，从而可以分析座椅参数和悬架参数对振动响应的影响。但对于这种单轮模型，仅仅处在定性分析的层面。随着计算机技术的发展，根据弹性动力学理论可以方便的建立车辆多自由度振动模型。模型自由度数越多，模型求解精度越高。图2建立了一个四轮八自由度模型：其中前后轴的垂向振动和绕X轴的侧倾角振动共四个自由度；车身质量沿Z轴的垂向振动和绕X轴的侧倾角振动和绕Y轴的俯仰角振动，共三个自由度；最后一个自由度是座椅沿 Z轴方向的垂向振动。这个八自由度三维空间动力学模型，虽然能够很好的模拟车辆振动状态。但是需要建立一个 8×8矩阵描述其数学模型，其中所需要的一些结构参数测量起来非常困难，计算过程也非常复杂，因此仿真起来比较困难[3]。当考虑汽车车架变形引起车体变化时，汽车自由度数还要增加。这样虽然求解精度增加，同时会使得计算更为复杂。

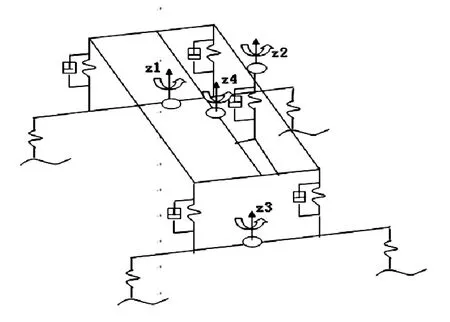
图2 车辆四轮八自由度仿真模型

2 车辆振动试验研究方法

2.1 时域分析法

振动时域分析方法是车辆振动分析领域的简易方法。时域波形比较直观、形象，可以简单、快捷的提取波形相关信息，分析振动的典型特性，从而定性的判断振动的量级、振动规律等信息。为了更精确提取振动波形，首先要对振动信号的时域数据进行如下处理。

振动测试时的信号数据，由于受到温度、仪器干扰，实测的数据值常常会偏离基线。偏离基线的数据常量称为趋势向。趋势项的大小对后端数据处理影响很大，在数据处理之前应该把它去掉。常用的消除趋势项的方法是多项式最小二乘法。对消除趋势项后的数据还要进行降噪处理，经过消除趋势项、降噪后的数据才更逼近真实数据。Matlab中提供了Detrend函数去除直流分量和线性趋势向。消除线性趋势项时需要指出两个线性部分共有的的坏点[4]。

数字滤波技术是去除振动信号噪声最常用的方法，其中无限长冲击响应（IIR）滤波器是最常用的滤波器，因为它具有通带内最平坦的幅度特性。Matlab中提供了buttord、butter函数设计Butterworth 滤波器设计函数。其中buttord函数设计滤波器阶数和截止频率。Butter函数使用设计的阶数和截止频率设计滤波器。图 3是阶数为 44，截止频率为 200Hz的巴特沃斯滤波器的频响函数。

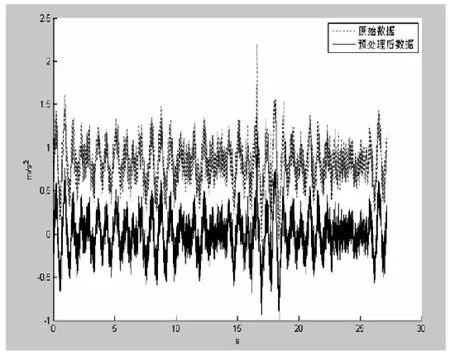
图3 数据预处理对比曲线

处理后的试验数据，包含的时域信息更为精确。在时域分析中，采用的参数有最大值、最小值、均值、均方根值、方差、脉冲因子等数据。每个参数代表的信息不一样。均值用来评价信号是否稳定。表征振动信号的中心波动，代表信号中的直流分量。均方根值是对信号的平方和再平均取开方，反应信号的能量大小[5]。脉冲因子反应振动脉冲的频率。

2.2 频域分析法

频谱分析法是车辆减振试验研究基本方法。在振源识别、减振降噪技术中应用非常广泛。我们常用的方法有幅值谱分析法、功率谱分析、传递函数分析、相干分析法，这些方法对我们研究振动特性非常有效。下面我们重点介绍幅值分析法与功率谱密度分析法在减振领域内的应用。

2.2.1 幅值谱分析法

由傅里叶理论可知，一个周期信号经过FFT变换后，可以得到的幅值谱是一个离散的信号。非周期信号经过FFT变换后，信号会连续的分布在一定的频率范围之内。幅值谱分析可以方便的把信号由时域下的分布变换到频域下的分布。幅值谱可以代表谐波频率时域信号的有效值，是时域信号各谐波的幅值随频率的一种线性分布。图4显示，经过对驾驶员座椅处的振动信号进行分析，发现 30Hz处的振动能量较大，说明在这一振动频率的振动分量对整个信号的影响最大[6]。

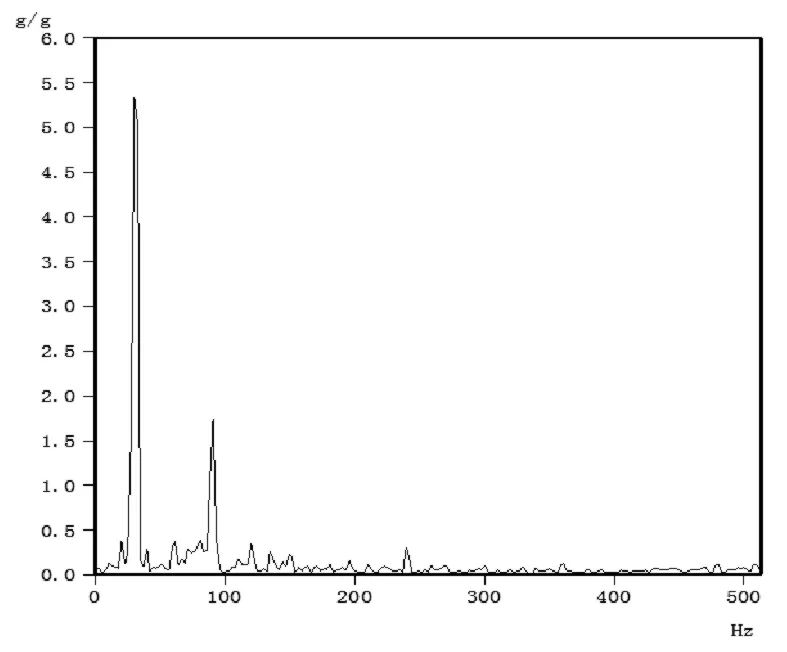
图4 FFT幅值分析法

2.2.2 功率谱分析法

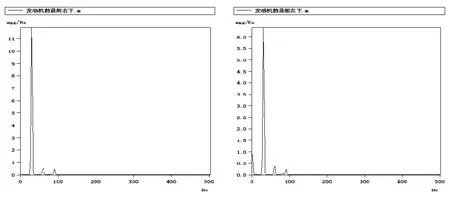
图5 前部悬置与发动机座椅处的互功率谱密度曲线

功率谱分析是研究随机信号频率分析非常重要的方法。其中自功率谱表示单位频带内信号功率随频率的变化情况，也就是说它反映了信号功率在频域的分布状况。功率谱线覆盖的总面积数值上等于信号的总功率。互功率谱可以描述频域内两个信号X（t）和Y(t)在频域内的相互关联程度。图5所示为被试车辆怠速 600rpm工况下，车架悬置处与车厢后排座椅地板处振动响应的互功率谱曲线。从图示可以看出，发动机前悬架右边相比左边和座椅处的振动量相关性要大。由于右部前悬置没有对发动机的质量扭矩进行有效地衰减，造成了振动能量通过车架传递到了车厢地板[7]。

3 总结

在车减振问题分析中，是一个非常系统的问题。为了解决一个问题，我们往往既要进行仿真分析，也要进行试验研究，提出一种合理的解决方案。随着计算机技术的发展，我们往往可以借助Matlab、Adams、ANSYS分析软件方便地进行建模分析，得到精确结果。借助时域、频域分析法，找到振动源以及引起振动的主要原因，从而进行改进。本文从理论、仿真、试验三方面进行系统阐述，提出了一些最常用的振动分析方法，为工程人员提供参考。