数形结合思维与高中物理解题教学的融合分析

徐建平

(江苏省赣榆第一中学 222100)

在高中物理教学中，教师曾提过很多种解题方法，也曾向我们验证过方法的具体操作过程，如顺序观察法、理顺制约关系及循因导果等，这些方法在实际解题过程中都展现出了非常有效的作用.但整合以往解题经验可以发现，不管是哪种解题方法都可以从数形结合的思维入手进行分析.下面对数学结合思维在高中物理解题教学中的应用进行深层研究.

一、高中物理与数形结合

1.高中物理教学特点

对比初中时期学习的物理知识，高中物理看起来更加抽象和理论.在教师看来，物理学属于定量的科学，物理学中的事物和事物之间的关系可以 依据代数式来展现，且不管我们是否可以感受到事物间的客观形态，都能依据某种“形态”体现出来，因此在解决不同类型的物理问题时，都可以引用数形结合的思维进行研究.

2.数学结合概念分析

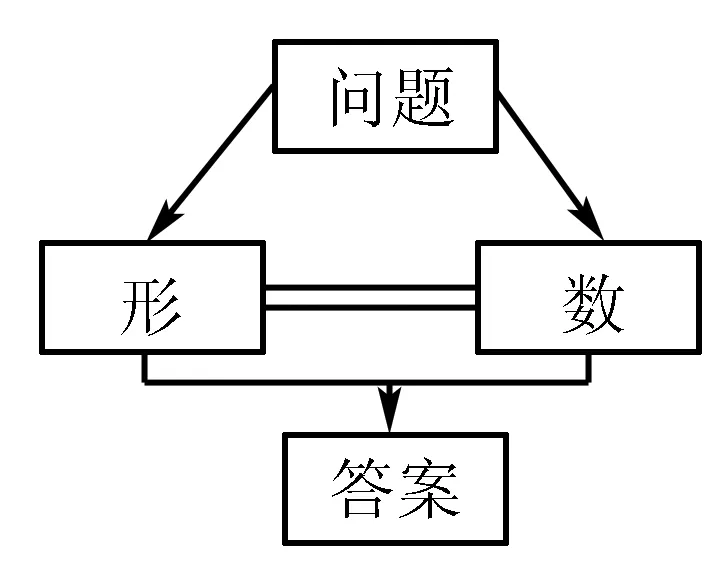
其源自于数学两种基本要素“数”和“形”的结合.在“数”和“形”的整合研究中，可以让问题变得更加简单.从广义角度分析，“数”和“形”属于辩证统一的问题，数形结合思想可以引用到所有课程中.在解决问题的过程中，用代数式来精确表达问题，也可以通过图形图像来直观表达，两者优势互补，可以让解题变得非常简单.具体解题形式如图所示.

二、数形结合思维在高中物理解题中适用的题型

1.图形选择题

选择题是高中物理解题教学的基础，也是依据数形结合思维解题的常见类型.一般情况下，选择题会为学生提供已知的图像，促使学生可以在研究图像的基础上进行思考，并选择正确的内容.在这类问题中，学生需要结合题干中给的已知条件，绘制正确的图像，并结合所绘图像与ABCD四个选项进行对比分析，排除错误答案，选择正确选项.了解实践案例可知，在高中物理选择题中推广数形结合思维，不但可以让学生依据转变急死俺获取所需物理量，而且可以帮助学生结合各个物理量构建正确的图像关系，进而明确更多的未知数.

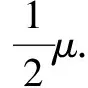
A.在F<2μmg时，A、B都相对地面静止

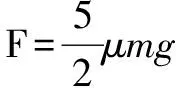
C.在F大于3μmg时，A相对B滑动

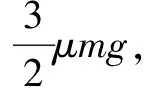
2.画图题

这类问题和选择题都属于结合物理量间的关系画出正确的图像，但后者可以让学生通过对比分析排除错误选项，缩小正确答案的范围.作图题通常情况下不会给学生提示，需要他们在明确已知条件的基础上，分析各个物理量间的关系，而后计算图形中其他参数和面积，并画出横纵坐标，确定图像中横纵坐标代表的物理量，了解图像中物理量的正负含义.同时，还要研究不同阶段函数形式的图线代表的物理过程，明确图像的物理含义，而后引用对应的物理公式、理论等内容进行深层探索.在对物理图像实施定量计算时，学生要认识到图像展现的各个物理量间的函数关系，而后明确图像中隐藏的条件关系，标出图像中包含的各类信息，判断横纵轴上的截距代表的物理意义，并引用对应的物理规律实施计算.

例2 (多选)如图2(a)所示，以物块在t=0时刻滑上固定斜面，其运动的v-t图线如图2(b)所示，如果重力加速度及图中的v0、v1、t1都是已知量，那么可以求出( ).

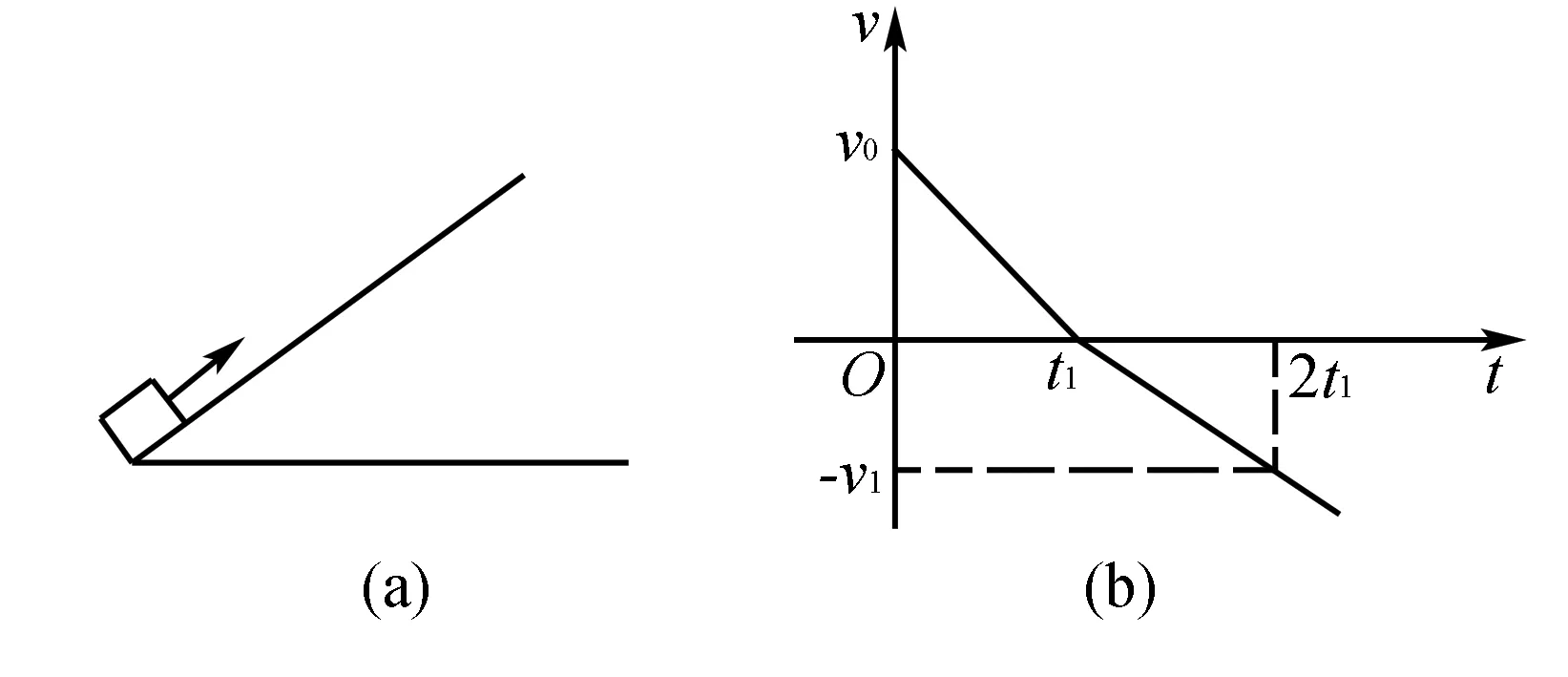
图2

A.斜面的斜角

B.物块的质量

C.物块与斜面间的动摩擦因数

D.物块岩斜面向上滑行的最大高度

解析 由图2(b)可知，物体先向上减速到达最高时再向下加速；图象与时间轴围成的面积为物体经过的位移，故可求出物体在斜面上的位移；图象的斜率表示加速度，上升过程及下降过程加速度均可求，上升过程有：mgsinθ+μmgcosθ=ma1；下降过程有：mgsinθ﹣μmgcosθ=ma2；两式联立可求得斜面倾角及动摩擦因数；但由于m均消去，故无法求得质量；因已知上升位移及夹角，则可求得上升的最大高度；故选：ACD．

3.图形转换题

这类问题属于高中物理解题时引用数形结合思维的另一经典题型.了解以往高中物理习题类型可知，很多图像看起来没有规律，但学生若是可以合理引用数形结合思想进行研究，促使物理图形转变为函数图像，就可以获取新的解题思路，这对提升解题效率和质量而言具有积极作用.在新课改教学理念提出，教师不但要引导学生熟练掌握所学理论知识，而且要熟练引用所学知识解决现实问题，只有这样才能促使学生全面发展，由此数形结合思维在图形转换题中的应用至关重要.

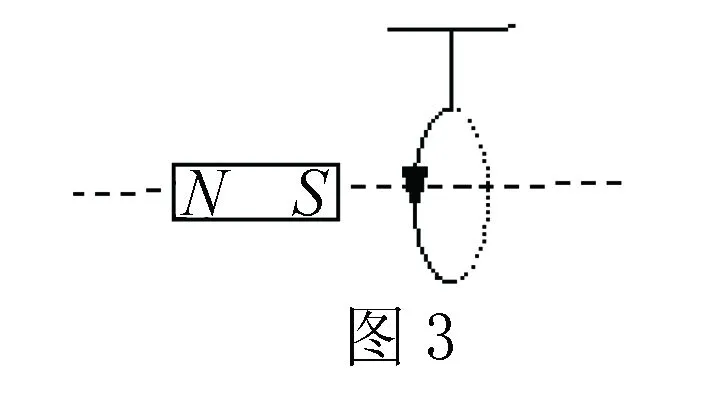
例 如图3所示，将轻质导线依据绝缘细线悬挂在磁铁S周边，磁铁的轴线穿过线圈平面，在线圈通过如图所示的方向电流时，线圈是如何运动的？

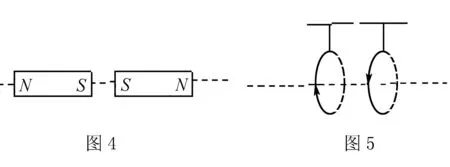
解析 在本题中，要想判断线圈是如何运动，最重要的依据左手定则研究，在条形磁铁感线中线圈所受的安培力.我们可以结合通电线圈磁感线和条形磁铁相似.将通电线圈转化为条形磁铁，具体如下图4所示.或者是将条形磁铁转变为线圈，具体如图5所示.由此，可以判断出线圈向右偏.

综上所述，在物理解题过程中，依据数形结合的思想解决物理问题，一定要结合具体情况选择适宜的数形结合方法，以抽象、复杂化的物理图形问题为例，学生可以选择“形”的数解方式进行操作.又如在解决各数关系过于繁琐的物理问题时，选择可以选择“数”的型化方法进行解决，以此在优化学生物理解题能力的基础上，拓展他们的思维空间.