例谈二项式定理高考热点题归类及解法

崔鸣岐

(北京市第十二中学 100071)

一、二项式展开式

1．二项式展开式的正用

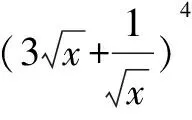
解法1 原式

二项式展开式中有三个量，它们是二项式的项、二项式的指数、展开式，题目已知二项式的项、二项式的指数求展开式即三个量的关系的知二求一，解法1直接用二项式定理展开从而求解.

题目解法2化简后再展开的求解方法.化简后分子转化为已知二项式的项、二项式的指数求展开式即三个量的关系的知二求一，从而再用二项式定理展开使问题得以解决.

点评 熟记二项式定理,是解答与二项式定理有关问题的前提条件,对比较复杂的二项式,有时先化简再展开更便于计算.

2.二项式展开式的“逆用”

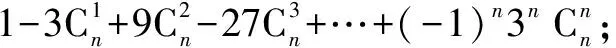
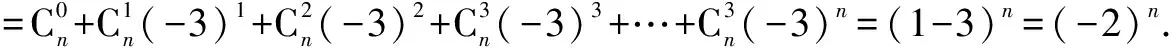
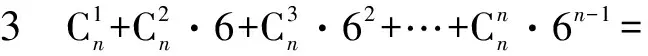
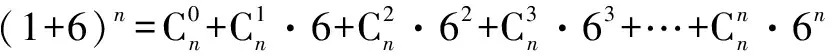
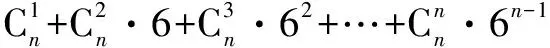
二项式展开式中有三个量，它们是二项式的项、二项式的指数、展开式，我们采取先将变形转化为展开式再解答的解题步骤.将变形转化为展开式后题目就转化为已知展开式、二项式的指数求二项式的项即三个量的关系的知二求一的常规题.

点评 逆向应用公式和变形应用公式是高中数学的难点,也是重点,只有熟练掌握公式的正用,才能掌握逆向应用和变式应用.

二、通项公式

1．求展开指定项的系数

A.15 B.20 C.30 D.35

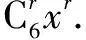
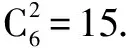
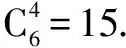
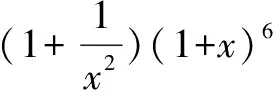
已知二项式求展开式指定项的系数, 直接利用二项式定理的通项公式求解即可．

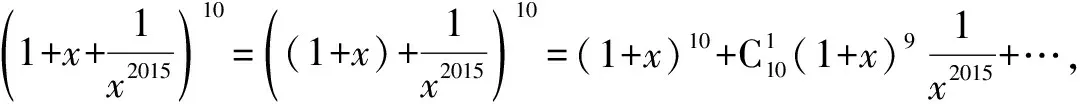
答案：45

对于三项式问题一般先变形化为二项式再解决．

2．求二项式的指数

例6 (2017年山东)已知(1+3x)n的展开式中含有x2的系数是54，则n=____.

解 (1+3x)n的展开式中通项公式：

∵含有x2的系数是54，

∴r=2．

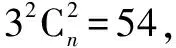
解得n=4．

故答案为：4．

已知展开式指定项的系数求二项式的指数，需利用二项式定理的通项公式转化为方程从而使问题得以解决．

3．求二项式的项或项的系数

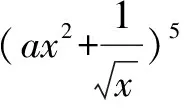
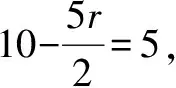
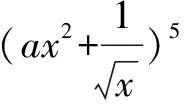
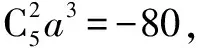
已知展开式指定项的系数求二项式的项的系数，需利用二项式定理的通项公式转化为方程从而使问题得以解决．

点评 该类题考查二项式定理通项公式的应用, 已知二项式求展开式指定项的系数, 直接利用二项式定理的通项公式求解即可；已知展开式中指定项的系数求二项式的指数或求二项式的项的系数，需利用二项式定理的通项公式转化为方程从而使问题得以解决；对于三项式问题一般先变形化为二项式再解决．过程中注意(1)二项式系数与系数的区别;(2)表示第r+1项.

三、二项式展开式系数的性质

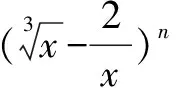
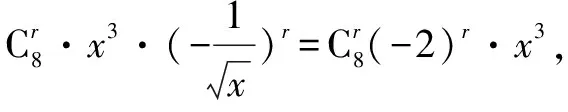
点评 该题考查二项式定理性质系数的应用,二项式定理性质中二项式系数的和为2n.已知系数之和，利用二项式定理性质构造方程求出二项式的指数，进一步利用通项公式求出展开式指定项常数项.

例9 (2015高考湖北)已知(1+x)n的展开式中第4项与第8项的二项式系数相等，则奇数项的二项式系数和为( ).

A.212B．211C．210D．29

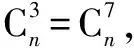
答案:D.

二项式性质的学习过程中对高考近几年热点题目根据知识点进行归类，在充分利用分类法学习的同时也兼顾到分类的不重不漏原则，才能做到在跳出题海的同时使复习更系统更全面.二项式展开式应用的题目解答过程中我们可以看出二项式展开式中有三个量，它们是二项式的项、二项式的指数、展开式(或展开式的变形，若是展开式的变形那么我们首要做的是将它转化为展开式)，无论是二项式展开式的正用还是逆用都可以看作在利用三个量的关系的知二推一，也就是利用转化思想方程思想使问题得以解决，这种解决问题的方法同样用在通项公式、二项式展开式系数的性质应用的相关题目的解答中.分类思想、转化思想、方程思想解决问题的思想方法若用到数学学科其他知识或其他学科知识的问题解决中都可以使问题解决达到事半功倍的效果.