一道高考试题的探究与溯源
2018-12-27 08:21黄旭东
数理化解题研究 2018年34期
黄旭东
(湖北省黄石市第一中学 435000)
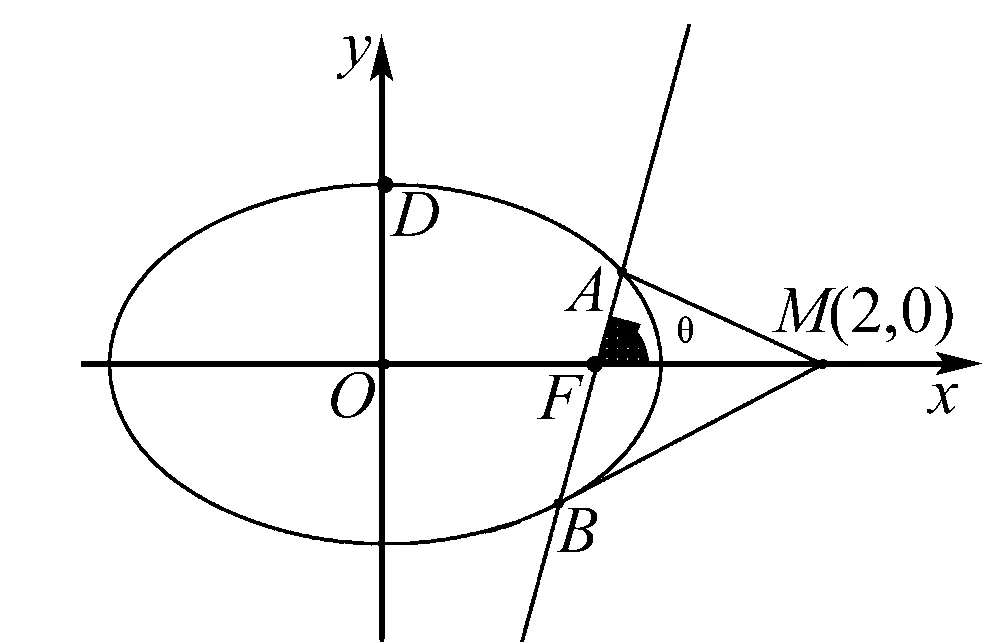
一、试题呈现(2018年新课标1中20题)
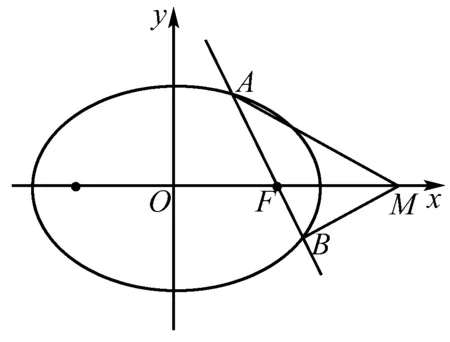
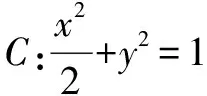
二、试题探究
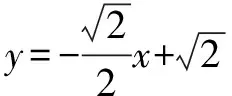
(2)(官方解答)当l与x轴重合时,∠OMA=∠OMB=0°;
当l与x轴时垂直时,OM为AB的垂直平分线,所以∠OMA=∠OMB.
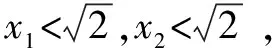
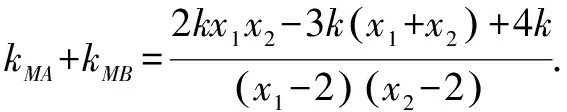
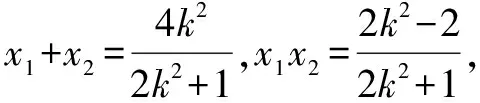
对(2)下面从不同的视角进行探究,作出几种不同解答.
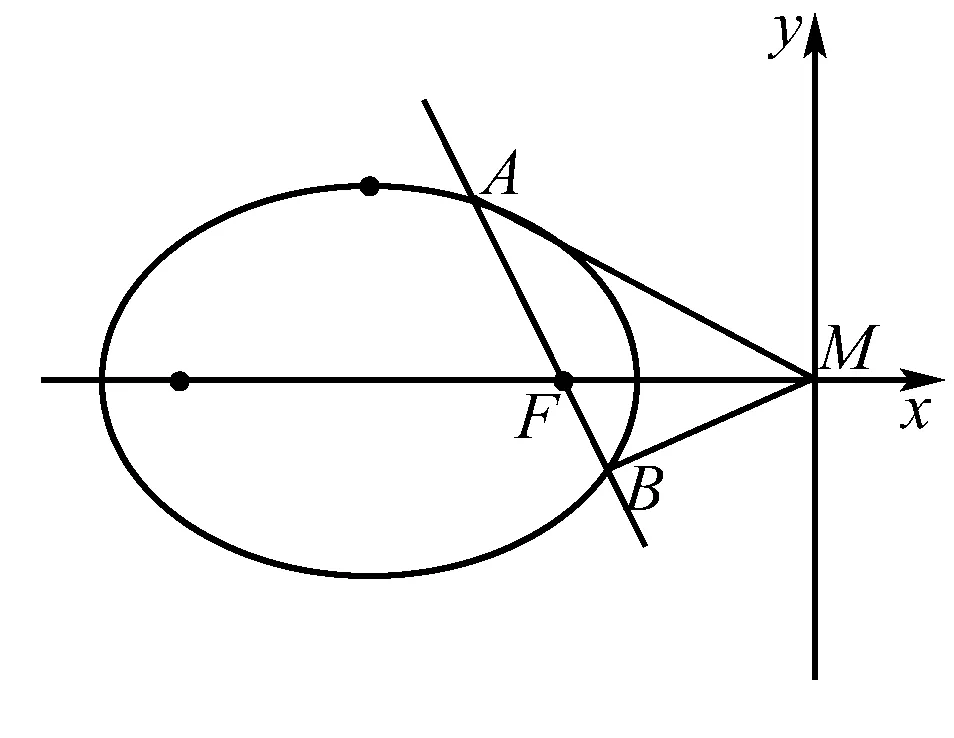
视角一 考虑到若将坐标系坐标原点平移到M点,则计算kMA+kMB时,利用韦达定理可较快计算出结果,可大大简化运算.要说明的是这种方法是对方法一的改进.
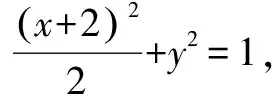
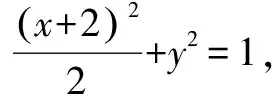
故MA,MB的倾斜角互补,所以∠OMA=∠OMB.
视角二 要证∠OMA=∠OMB,考虑点A关于x轴对称点A′ ,则必有A′,B,M三点共线即可.
法2 (利用轴轴对称,证明三点共线)
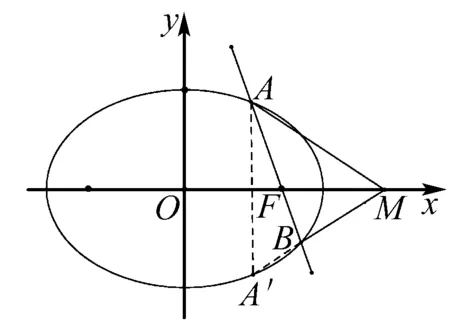
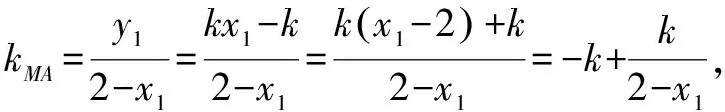
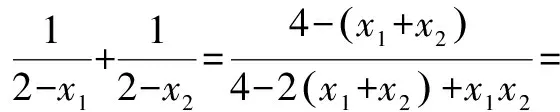
则kMA′=kMB,故M,A′,B三点共线.由于A(x1,y1)关于x轴对称点A′(x1,-y1),则∠OMA=∠OMB
视角三 巧妙构建过定点M(2,0)的二次齐次式,处理斜率问题.
法3 当l与x轴重合时,∠OMA=∠OMB=0°.
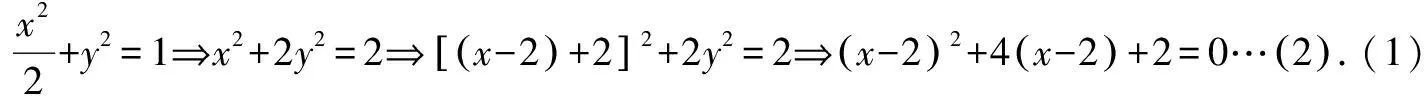
视角四 考虑角平分线性质,结合极坐标工具,可化成极坐标求解.
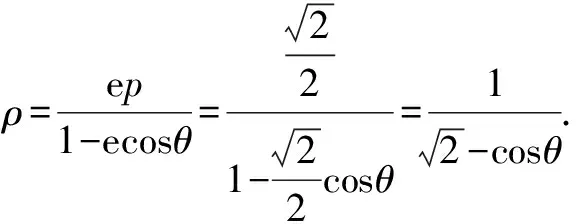
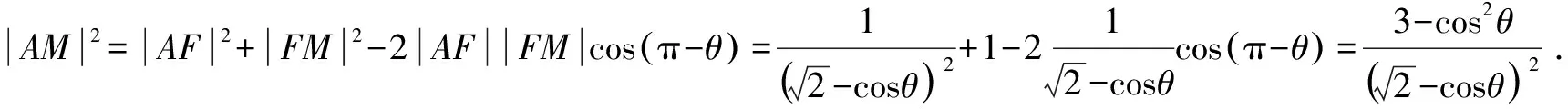
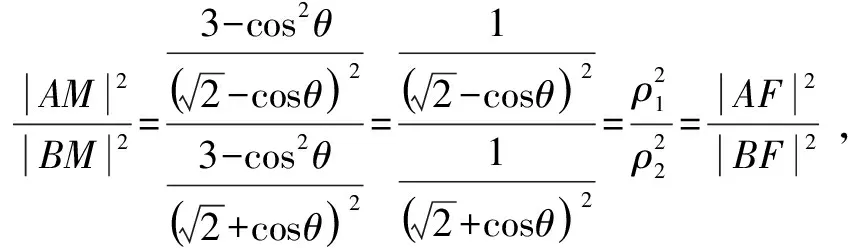
视角五 考虑角平分线性质,结合参数方程工具,可利用参数求解
法5 设直线l倾斜角为θ,则直线l的参数方程为
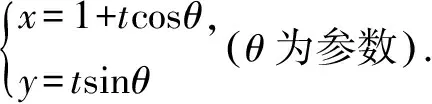
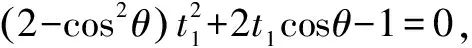
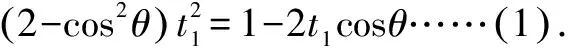
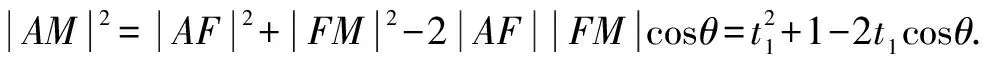
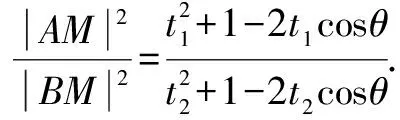
三、试题溯源
本题来源于下面定理
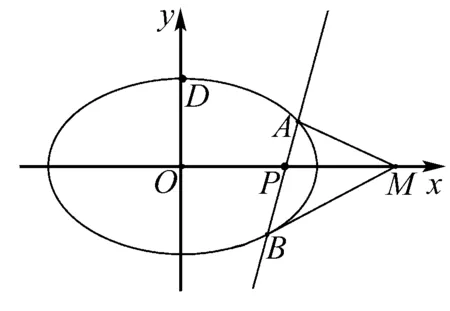
证明过程同上面方法相似,限于篇幅,此处略.同理类似上述性质可推广到双曲线与抛物线,即有:
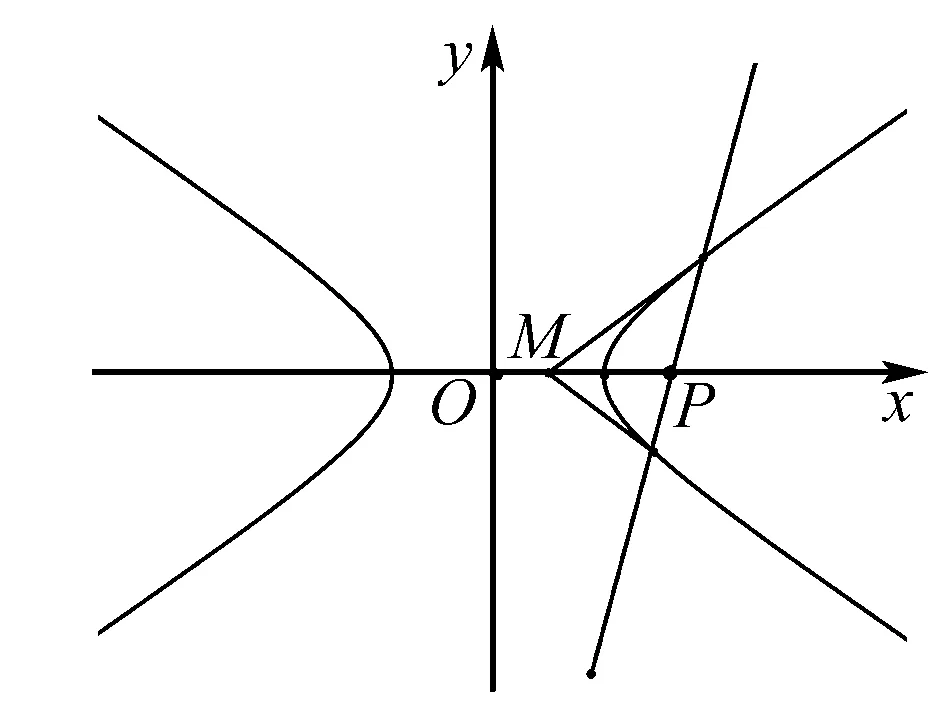
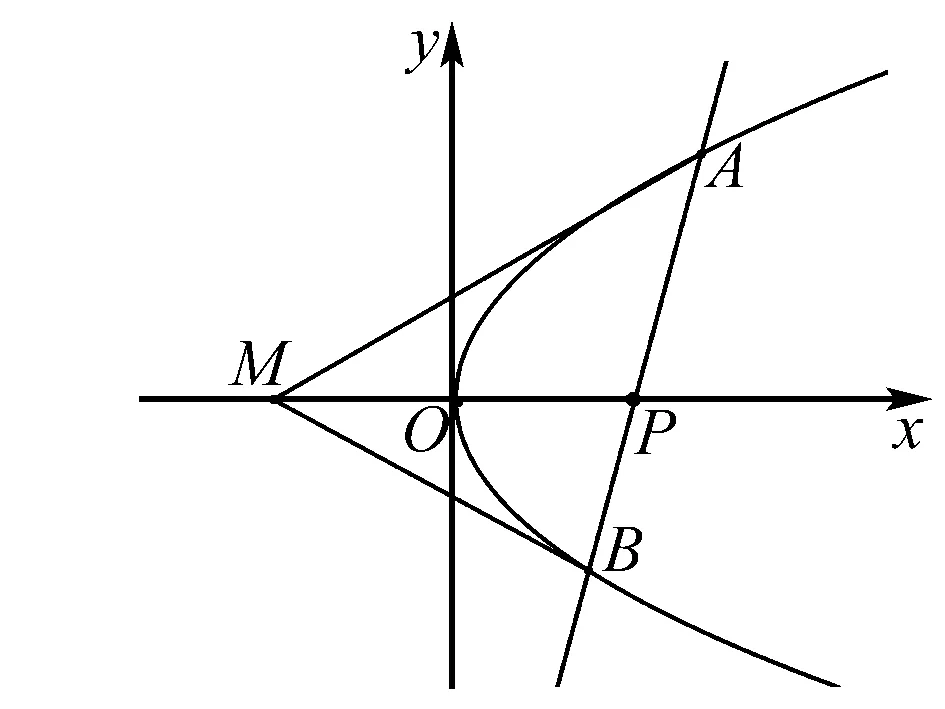
定理3 设抛物线:C:y2=2px(p>0),直线l过点P(t,0)与C交于A,B两点,点M的坐标为(-m,0) 则有∠OMA=∠OMB.
猜你喜欢
新高考·高一数学(2022年3期)2022-04-28
中等数学(2021年4期)2021-08-14
中学生数理化·高一版(2021年5期)2021-07-21
河北理科教学研究(2020年2期)2020-09-11
河北理科教学研究(2020年1期)2020-07-24
中学数学研究(广东)(2018年23期)2018-03-05
北京航空航天大学学报(2017年1期)2017-11-24
电子设计工程(2014年18期)2014-02-27
中学理科·综合版(2008年9期)2008-10-15

