超几何分布和二项分布区别探讨

何正文

(广东省肇庆市百花中学 526000)

超几何分布和二项分布是高中阶段最重要的两种离散型随机变量的概率分布，超几何分布和二项分布是人教A版选修2-3第二章随机变量及其分布列中的两种重要分布，也是高考概率统计大题中重点考查的内容，二者的区别难以分清.本文就二者的联系和区别进行思考.

一、定义把握

先看一下课本给出的两种分布的概念：

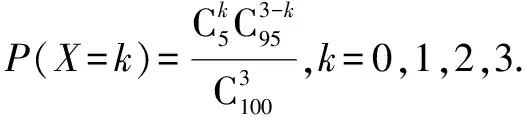
这个概念的给出还是挺耐人寻味的，出自正品次品混合取件的例子，有点类似于判例法，这在高中课本中仅此一例.如果严格按照定义，要先计算分布列，然后才能判定是否服从超几何分布，这样本来也无可厚非，但对于解题来说可能就不太方便了，更多的时候我们需要先判定再计算.而且定义中引入了大量字母，公式也略显复杂，对学生来讲难以把握.简单总结就是：总体较少且分两类，则样本中关注类的个数服从超几何分布.依据这个简易概念去判定就会方便多了.

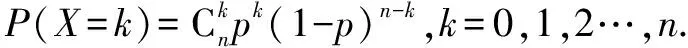
这个概念相对较好把握，简单总结就是：独立重复试验中成功次数服从二项分布，关键就是独立重复试验的判定.

二、两种分布的联系和区别

这两种分布从概念来看有很大的不同，甚至看不到有什么相似之处，但在具体问题中的就不像看定义这样简单易区分了.我们不妨就用课本中的例子通过改编来体会一下二者的区别.

例1 在含有M件次品的N件产品中，按下列取法依次取n件，求取到的次品数X的分布列：

(1)不放回地取；

(2)有放回地取.

分析 第(1)问中，不放回地取，最终取出n件，总体显然分为正品和次品两类，则所取n件样本中次品类的个数一定会服从超几何分布.而第(2)问中，有放回地取，每次取出后放回，则每次取出次品的概率相同，是n次独立重复试验，则取到的次品数X一定会服从二项分布.

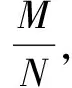
通过两道小题的比较分析，我们不难得到初步结论：当总体个数较少时，“有放回”地取件，目标类的个数服从二项分布，“不放回”地取件，目标类的个数服从超几何分布.

再看一个例子.

例2 二十世纪50年代，日本熊本县水俣市的许多居民都患了运动失调、四肢麻木等症状，人们把它称为水俣病.经调查发现一家工厂排出的废水中含有甲基汞，使鱼类受到污染，人们长期食用含高浓度甲基汞的鱼类引起汞中毒.引起世人对食品安全的关注.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.00ppm．罗非鱼是体型较大，生命周期长的食肉鱼，其体内汞含量比其他鱼偏高．现从一批罗非鱼中随机地抽出15条作样本，经检测得各条鱼的汞含量的茎叶图(以小数点前一位数字为茎，小数点后一位数字为叶)如下：

罗非鱼的汞含量(ppm)01321598732112354

(1)在这15条样本鱼中，任取3条，记η表示抽到的鱼汞含量超标的条数，求η的分布列及Eη.

(2)以此15条鱼的样本数据来估计这批鱼的总体数据．若从这批数量很大的鱼中任选3条鱼，记ξ表示抽到的鱼汞含量超标的条数，求ξ的分布列及Eξ．

分析 (1)由题知，15条鱼作为样本总体，个数较少且明显分为汞含量超标和汞含量不超标两类，个数分别为5条和10条，任取3条，则这3条中的汞含量超标类的鱼的条数η显然服从超几何分布，η的可能值为0，1，2，3.

则η的分布列为：

η0123P(η)249145912091291

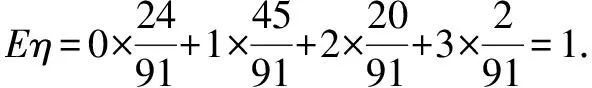
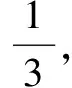
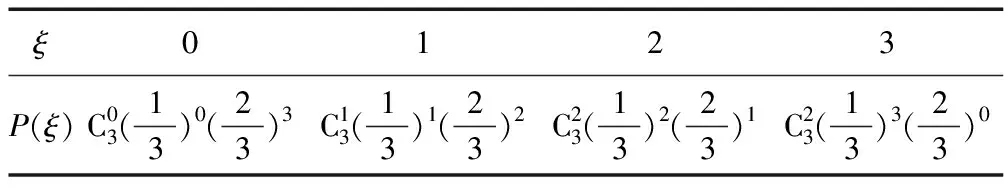
ξ0123P(ξ)C03(13)0(23)3C13(13)1(23)2C23(13)2(23)1C23(13)3(23)0

所以Eξ=1.

通过对例2的分析，我们发现考察对象从样本变到总体后，分布类型由超几何分布变为了二项分布！

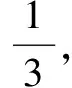
我们更愿意通过对大量鱼群中的一条鱼“漠视”，忽略它对鱼群的影响，这样概率的计算就会变得容易很多，我们的统计和计算工作都大大地简化了！超几何分布就近似“变为”了二项分布，这个变化其实是两种分布概率的一种近似，对应取值的概率用两种分布去计算肯定不相等，但随着总体趋于无穷大，我们可以推测，他们的概率会越来越接近！在本例中，从有限到无限，从超几何分布到二项分布，客观上并没有转变，其实是我们主观选择的结果！我们选择了一个“错误”的分布来减少计算量！这也是不得已而为之，而这也是用样本估计总体的一个不得已的选择.

所以我们对两种分布的进一步结论是：考察对象“有限”时服从超几何分布，“无限”时则服从二项分布.

三、期望值的巧合

在例2中其实还有一个很有意思的地方我们可以关注一下，两种分布的期望值是相同的！这是不是巧合呢？

通过刚才的分析我们已经知道，当总体数目非常大时，超几何分布与二项分布对应取值的概率近似相等，那它们的期望也是近似相等的，这很好理解.那为什么总体数目非常少的时候，超几何分布的期望值算出来和二项分布也是相等的呢？我们还是继续从例2中体会一下.

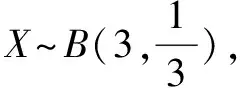
这一个结论还可以通过代数的方法进行证明，过程如下:

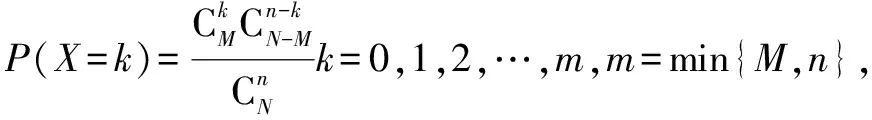
通过上面的思考与证明，我们发现两种分布的期望确实是相同的！

超几何分布与二项分布这两种重要的离散型随机变量的分布之间关系基本已经理清了，“有放回”和“无放回”的区别，“有限”和“无限”时的转化，期望值的“巧合”，无不体现出二者的千丝万缕的联系.