带时间窗的快递包装回收车辆路径优化研究

邓学平，薛 莹，田帅辉

(重庆邮电大学 经济管理学院，重庆 400065)

0 引 言

近几年，网上购物的普及和电商平台的飞速发展促使了快递行业极速前进。相关管理部门调查显示，2016年中国快递总量高达312.8亿件，比去年增加51.7%，总收入达到4 005.00亿元，同比增长44.6%。截止2017年08月，快递业务总收入为404亿元，比去年同期增长27.2%。然而，伴随快递企业业务量的飞速增长，随之产生的废弃包装材料回收问题日益突出，对我们的生活环境造成了严重影响[1-2]。快递回收问题主要包含废弃包装回收及回收车辆路径的优化2个方面。

对于包装废弃物回收问题的相关研究，文献[3]根据回收主体的不同，分别构建了由制造商负责回收的集中决策模型和由第三方企业负责统一回收的模式，并在随机需求环境下，分别计算出不同决策情况下相应的最优回收价格，并进行比较分析；文献[4]基于目前包装物逆向物流的3类回收主导模式(垃圾站回收、包装生产商回收、第三方物流企业回收)，提出了自营物流回收模式；文献[5]加入了政府奖励机制和物流的负外部约束引导企业来布局绿色逆向物流网络；文献[6]分析了构成逆向物流的不确定因素，并提出了考虑提前期的混合整数规划模型，并且采用遗传算法对规划模型进行求解验证；文献[7]充分利用包装废弃物逆向物流网络的优势，积极发展和研究包装废弃物逆向物流，使其高效运作；文献[8]研究了关于包装废弃物的逆向物流，考虑到多类型包装废弃物同时进行回收，以成本最小为目标构建数学模型。

对于回收车辆路径优化问题，带时间窗的车辆路径问题(vehicle routing problems with time windows, VRPTW)国内外学者进行了研究，文献[9]采用启发式与合并式相结合的交叉算子，融入了爬山算法和自适应变异机制，设计了改进遗传算法求解VRPTW问题；文献[10]构建了关于硬时间窗的随机动态问题模型；文献[11]设计了局部优化框架，并结合遗传算法解决了带时间窗的车辆路径问题；文献[12]考虑到分队被服务的优先关系，结合时间窗和距离的权重因素，引入交叉算子，设计了改进的遗传算法；文献[13]在染色体结构中融入分组信息，辅以交换局部搜索技术，构造了一种混合遗传算法；文献[14]采用三复本锦标赛的选择方法和改进的启发式交叉算子，提出了改进遗传算法求解车辆路径问题。

现阶段对于快递包装物的回收研究主要在改进包装形式，改进运输车辆路径[15]等方向，对于快递包装回收过程中用户的满意度方面并没有太多研究，本文基于此将时间窗限制运用到快递包装物回收体系中，并增加顾客满意度问题进行研究，以推进快递包装回收效果，响应国家绿色物流政策。

1 问题描述及模型

1.1 问题描述

带时间窗的快递包装回收车辆路径问题可详细描述为快递企业根据区域内客户回收意愿，在已知回收中心条件下，寻找满足客户意愿及车辆运输最佳线路，即寻找满足总成本最小、在客户要求时间内到达的车辆最佳运输线路。

实际情景是将回收系统中的节点简化为回收中转站、客户节点。回收网络结构图如图1所示，车辆从回收中转站按时到达客户点提供服务，最后回到回收中转站，形成闭环网络。本文的目标函数是实现最小车辆运输总成本，包括运输成本、处理成本、回收成本以及时间惩罚成本。

图1 回收网络结构图Fig.1 Recycling network structure

1.2 模型假设

1)尽管物流包装大小不一，但为了方便研究，本文将所有包装均视为一类。

2)每个客户节点由一辆车进行服务，车辆完成一条回收路线后返回中转站，并且将所有回收的包装运回。

3)车辆在服务过程中始终满足容量约束，因为每个客户节点都有固定的时间限制，早到或者晚到都会产生相应的时间惩罚成本。

4)假设已知回收中转站和客户节点的数量、位置、回收数量、服务时间窗、单位包装处理费用、回收费用、车辆单位运输费用等。

1.3 参数定义

1.3.1 参数定义

本文模型中的已知参数含义如表1所示。

表1 参数定义

1.3.2 决策参数定义

本文模型中决策参数的含义如表2所示。

表2 决策参数

1.4 目标函数定义

1)运输总成本最小的目标函数为

(1)

(1)式中：等式右边第1项表示车辆k从i客户点到j客户点所产生的运输费用；第2项表示一天内回收的所有快递包装物在处理中心产生的总处理成本；第3项表示公司在i客户点所支付给客户的费用；第4-5项表示回收车在i客户点服务提早或推后所造成的时间成本；第6项表示回收车k服务时间超过每天规定时间的成本。

2)约束条件

①车辆k的回收容量不可以超过该车辆最大载质量，即

(2)

②时间窗限制，车辆k确保能够在客户节点期望的时间为其服务。

lj=max(aj,li+tij+ei),i,j∈H

(3)

ai≤li≤bi,i∈H

(4)

(li+tij+ei)xij-lj≤0,i,j∈H,k∈V

(5)

③各已知参数的取值范围

xij=0,1,i,j∈H,k∈V

(6)

zr=0,1,r∈G

(7)

yij=0,1,i∈H,j∈G

(8)

Uij≥0,i∈H,k∈V

(9)

2 模型求解

为解决带时间窗的回收车辆路径优化问题，利用改进的遗传算法对模型进行检验。本文将带时间窗定位—路径模型的求解过程转化为车辆运输路径最优问题，将染色体编码转化为车辆的运输路径，用基因表示回收中转站、客户节点，产生初始种群；设置时间惩罚函数(客户满意度)对超过客户服务要求时间限制的车辆进行相应的惩罚，计算最小目标函数值，得到相应个体适应度；再对种群进行选择、交叉、变异，迭代若干次后，最终得到最优路径。

2.1 编码与解码

本文采用自然数编码方法[16]对带时间窗车辆路径优化问题进行编码操作。假设回收中转站拥有相同车型k辆，运输网络中有l个客户，则编码为0,i11,i12,…,i1s;0,i21,i22,…,i2t;0,ik1,ik2,…,ikw,0。其中，染色体相邻的2个0之间表示染色体中的一个子路径。9个客户节点同时需要3辆车来进行服务的编码为0514073680920，描述为第1辆车从回收中转站出发，经过客户节点5，1，4返回回收中转站，称为子路径1；第2辆车也从回收中转站出发，经过客户节点7，3，6，8返回回收中转站，称为子路径2；第3辆车从回收中转站出发，经过了9，2返回回收中转站，称为子路径3。相对应的配送路径如下所示(0表示回收中转站)：

子路径1：0-5-1-4-0

子路径2：0-7-3-6-8-0

子路径3：0-9-2-0

解码是编码的逆过程，本文将采用与编码相似的方式进行解码操作。根据载质量和时间窗双重约束对编码S进行划分，具体方法如下。

1)i=1；

2)开始第i条路线Ri=[0]，0为回收中心；

3)尝试将编码S中的第1个点加入Ri，如果加入Ri后车辆载质量和时间窗都满足，那么转下一步，否则i=i+1，转2)；

4)删除S的第1位编码，如果S空，那么转下一步，否则转3)；

5)输出各个子路径。

2.2 适应度函数

本文目标函数相对应的适应度函数[15]为

(10)

(10)式中：Fi是染色体i的适应度值；yi是染色体i的目标函数；pi是染色体i的惩罚值。

2.3 选择算子

对最优适应度函数值按从大到小的顺序排列，设定适应度值排前50%的保留至下一代，以防止更优路径方案被淘汰，然后使用轮盘赌法选择算子[17]。轮盘赌算子是一种运用个体适应度占种群中的比例来确定其下一代的方法。具体步骤如下。

步骤1计算种群中N个个体的适应度，并对适应度函数值从大到小进行排序，选择前M个(假设为种群规模的50%)个体进入下一代；

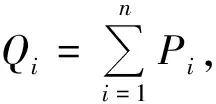
步骤3以[0,1]的随机数作为选择指针，若r≤Q1，则选择个体1；若r≥Qi，则选择个体i；

步骤4重复步骤3，直到产生N-M个个体。

2.4 交叉操作

本文选用2点交叉法[18]进行交叉，先随机抽取2个父代染色体A和B，选取2个自然数r1和r2，将父代A和B中第r1位至r2位的片段交叉，随之可以产生2个新染色体，最后对其进行修订，使得最后的染色体内没有重复。修订过程：父代A和B交叉产生新染色体后，将未进行交叉操作的染色体补齐到原染色体中，具体如图2所示。图2中，r1=2，r2=4。

图2 交叉操作Fig.2 Crossover operation

2.5 变异操作

为了父代的优秀基因可以遗传到下一代，需进行变异操作。变异操作是在运算过程中改变了其中部分基因的位置。本文采取2点互异[18]进行变异，首先产生2个任意自然数r1和r2，随后交换r1和r2的基因。例如r1=2，r2=4时，变异情况如图3所示。

图3 变异操作Fig.3 Variation operation

2.6 算法终止条件

当本文算法中的某个结果连续重复出现，或者算法进行了T次(T为设定的最大迭代次数)时，运算终止并输出最优解，并作为相对应的车辆运输路线。

2.7 算法灵敏度分析

遗传算法中有许多参数设置，参数的不同取值，对算法的最终结果及运行速度等都有一定的影响，包括种群规模、交叉概率、变异概率、迭代停止条件[19]等。除了算法设计中涉及到的参数外，车辆的运输成本也对算法具有一定的影响，以下详细阐述不同参数设置对算法的影响。

1)种群规模。算法的种群规模分别选取180，185，190，195，200，运行10次，取其平均值。其他参数设置：交叉概率为0.8，变异概率为0.1，停止迭代次数为1 000次，单位运输成本为1。不同种群规模的目标函数收敛图如图4所示。不同种群规模对算法的影响如表3所示。

图4 不同种群规模下，目标函数收敛图Fig.4 Objective function convergence chart under different population sizes

种群规模时间/s最优解收敛代数180190582.893185207582.7116190207440.2130195215593.6112200217447.6109

从表3可以看出，运行时间随着种群规模的增加而逐渐延长，但幅度并不大；最优解随着种群规模的变化也在变化，但没有明显的变化趋势；收敛代数随着种群规模的不断增加，呈现先增大后减少的趋势。

2)变异概率。算法中的变异概率分别取0.06, 0.08，0.1，0.12，0.15。其他参数设置为种群规模为200，交叉概率为0.8，停止迭代次数为1 000次，单位运输成本为1。变异概率对算法的影响如表4所示。

表4 变异概率对算法的影响

从表4可以看出，随着算法变异概率的改变，运行时间的变动幅度比较小；对于最优解、迭代次数的变动幅度较大，并且没有一个固定变化趋势。当变异概率过小时，算法比较容易收敛于局部最优；当变异概率过大时，算法搜索的范围扩大，使得迭代次数增多，从而影响算法的优化效率。

3)运输成本。模型中的运输成本分别取0.5，1，1.5；种群规模为200；变异概率为0.1；交叉概率为0.8；停止迭代次数为1 000次。运输成本对算法的影响如表5所示。

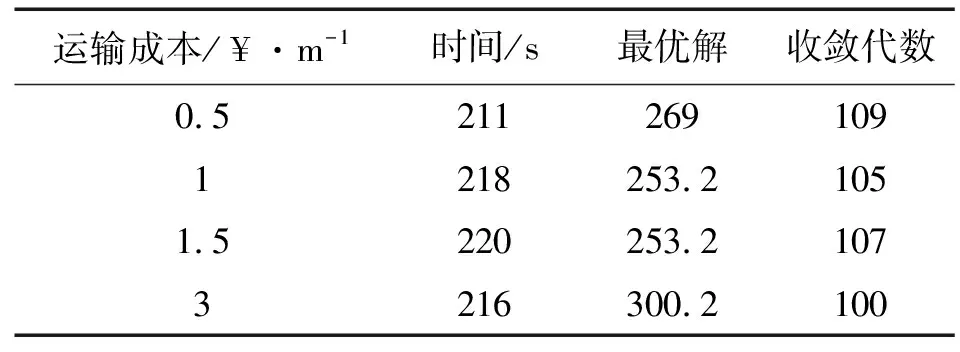
表5 运输成本对算法的影响

运输成本的变化对结果的影响主要体现在车辆的运行路径上，当运输成本选择越来越大时，车辆选择的运输路径会发生比较大的变化。即当一辆车的单位运输成本超过一定值时，启动另一辆车进行回收的总成本会低于继续使用这辆车的成本。

3 算例验证

3.1 数据生成与处理

假设D1为回收中转站，容量为100，19个具有回收需求的客户节点，同一种车型的车辆若干，容量15，回收车平均运行速度60 km/h，运输成本1 ￥/km，回收车辆早于客户要求时间到达的成本10 ￥/h，晚于客户要求时间到达的成本20 ￥/h，每个客户节点规定服务时长0.2 h，再处理费用Pr=0.02单位价格/单位回收产品；根据时间限制安排车辆对19个客户点执行回收服务，最终使得系统成本最小。节点具体的相应数据如表6和表7所示。

表6 回收中转站相应数据

表7 客户相关数据

注：开始时间与结束时间均以上午8:00为参考计算。

3.2 结果分析

利用Matlab软件进行仿真，采用遗传算法的参数设置为种群规模为200，交叉概率为0.8，变异概率为0.1，迭代停止条件为1 000次。带时间窗的快递包装回收车辆路径问题仿真结果为需要3辆相同车型的回收车辆对这19个客户点进行回收，最小成本为￥430.78，达到最优解的迭代次数为129次。3辆回收车的路径如表8所示。最优配送方案仿真结果如图5所示。

表8 回收车辆路径

从图5可以看出，在算法优化的初步阶段，函数曲线急速下降，但随着迭代次数的逐渐增加，曲线变得平缓，并在迭代次数为129时收敛于最优解￥430.78。由于在优化开始时，随机产生的初始群适应度很低，因此，得到的最优解较差。随着优化的次数增加，目标函数慢慢接近最优解。该模型的目标函数收敛情况说明了本文的算法在该问题中是可行的，构建的模型是合理的。

图5 带时间窗最优配送方案Fig.5 Optimal distribution plan with time window

图6 不带时间窗最优配送方案Fig.6 Optimal distribution plan without time window

在同样的客户节点，不考虑客户时间要求的情况下，车辆的回收路线以及最小回收成本，求解本模型，结果如图6所示。

根据图6可以看出，在此次回收过程中，同时2辆车进行回收服务，回收总成本为￥324.79，最优回收路径如图6a。根据是否带时间窗的仿真结果，对比分析，如表9所示。

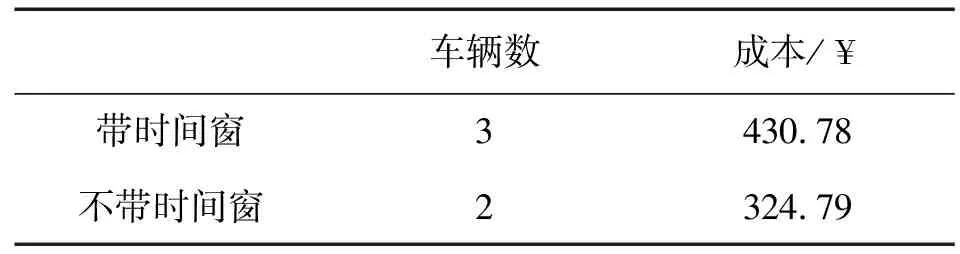
表9 带时间窗与不带时间窗结果对比

由表9可知，在考虑时间窗的情况下，由于车辆在行驶过程中需要满足客户的时间要求，车辆路径中出现了顾客服务先后顺序的现象，对没有按时到达客户服务的车辆会产生一定的惩罚成本，为了确保在规定的时间内进行回收服务，则需增加回收车进行同时服务，则会造成回收车实际载质量减少或车辆绕路行驶的情况发生，相应地回收车总行驶距离增加，从而造成了回收运输成本增加。但是，虽然车辆数量增加了50%，但成本只增加了32%，这意味着，增加相应的时间成本一方面可以提高企业的服务质量；另一方面对于顾客来说增加了其“购物”体验，即在规定的时间内由专业人员上门回收快递包装物可以增加顾客对其公司的服务满意度。

对于目前存在的物流体系，存在一种“物流效益背反”现象。快递企业为了达到成本最小化的目标，可能会降低企业服务质量，那么顾客对企业服务的满意度也会随之降低。对于许多企业来说，不考虑服务时间来回收快递包装物可以降低一定的成本，但同时也会造成顾客满意度低下的情况发生。但如果完全遵循顾客所要求的时间段来进行回收任务，可能会导致回收车载质量减少，数量增加随之而来的时间成本的增加，最终会造成回收成本的增多。因此，应该综合考虑成本与顾客满意度之间的关系，尽力达到理想平衡状态。

4 结束语

本文针对快递包装材料回收逆向物流体系，拟采用以快递企业为主体，将顾客满意度转换为时间成本加入目标函数中，从而以回收系统最小成本为最终目标建立一个受时间窗约束的定位—运输车辆路线模型。并设计了改进的遗传算法，在算法的种群规模、变异概率、运输成本方面进行灵敏度分析，验证算法的有效性。利用构建的模型以及设计的遗传算法进行算例分析，并通过Matlab软件运行仿真，获得本文带时间窗的快递车辆路径问题的最优路径，并与不带时间窗进行对比，结果表明，本文设计的模型及算法优化了回收路径、减少顾客等待时间，最大限度提高了顾客满意度。本文提出的观点为快递企业包装材料回收问题提供参考依据。本文在研究快递包装物回收问题中，没有考虑回收包装的大小问题，该问题可在以后的研究中进行改进。