CRSNs中基于传感器选择的高能效频谱感知算法

李 鹏，闵 慧

(1.湖南中医药大学 信息科学与工程学院，长沙 410208；2.湖南信息职业技术学院 计算机工程系，长沙 410200)

0 引 言

为了解决频谱资源稀缺和无线业务请求数量增加的问题，人们提出了认知无线电网络(cognitive radio networks, CRNs)[1]。在CRNs中，未经许可的次要用户(secondary users，SU)通过频谱感知技术可以适时地向专用于许可主要用户(primary users，PU)通信的带宽上发送数据，并且不会对PU的数据传输造成有害干扰。认知无线电传感器网络(cognitive radio sensor networks, CRSNs)作为CRNs的重要子集，是一种由配备了认知无线电能力的传感器节点组成的无线通信网络，通过适时接入可用的频谱资源解决了CRSNs中资源稀缺的问题[2-4]。

为了提高频谱感知的可靠性，协同频谱感知(cooperative spectrum sensing,CSS)[5-6]已被广泛应用于CRSNs的各种应用场景中。在CSS中，多个SU协同感知频谱并共同决定频谱上是否存在PU。CSS在提高频谱感知可靠性方面有显著的优势，但在CSS过程中如何降低传感器能耗是目前存在的一个主要问题。文献[7]提出了一种基于节点优先选择策略的协作认知传感器网络。首先定义了认知节点在感知空闲信道上的检测概率和虚警概率，通过概率约束条件来限制认知节点的感知性能下限,接着对认知节点进行能量分析，提出一种基于代价函数的决策规则，在满足网络所需要的频谱感知性能的条件下，对能耗更低的认知节点赋予更高的优先级，从而选择优先级别更高的认知节点参与网络的频谱感知，并限制了参与频谱感知的节点数量。然而，该方法假设所有传感器接收的来自PU的信噪比值相同，这在实际应用中并不存在。文献[8]基于隐马尔可夫模型(hidden markov model, HMM)对传统支持向量机(support vector machine，SVM)频谱感知算法进行了优化，采用多个分类器的集成来降低频谱识别错误和增强识别鲁棒性。文献[9]提出了一种传感器选择方法用于降低CSS的能量消耗。该方法根据传感器的检测概率和每次感知操作的能耗关系来优先考虑传感器。然而，这样的选择方法导致优先级较高、网络覆盖不完善的传感器不均衡地快速消耗能量。文献[10]周期性地计算所有传感器的剩余能量及其检测概率，动态地确定其参与CSS的优先级，最终得到参与CSS的传感器最优组合。该方法虽可保证感知精度，但需要大量的计算，复杂度较高，也不利于节省节点的能量。针对以上不足，本文提出了一种基于传感器节点选择的频谱感知算法用于降低CSS能耗，最后通过仿真实验验证了所提算法的有效性。

1 系统模型

为了便于描述，下面先介绍文中用到的相关概念。

定义1虚警概率：SU通过CSS认为频谱上有PU在通信，而实际上不存在PU的错误识别概率。

定义2检测概率：频谱上实际存在PU时，SU通过CSS正确检测出PU的概率。

考虑一个由N个传感器交织组成的CRSNs，sj(j=1,2,…,N)表示第j个传感器。传感器负责感知一些环境参数并将获得的信息传送给融合中心(fusion center, FC)。传感器采用目前典型的能量检测方法[11-12]进行频谱感知，如果传感器在频谱上未检测到PU的存在，则它可以适时地使用带宽，系统模型如图1所示。

图1 系统模型Fig.1 System model

在CRSNs中，PU占用频谱进行通信的时间通常是周期性的、离散的，即SU通过频谱感知技术可以分时地接入空闲频谱进行数据传输。因此，本文将能被传感器用来传输数据的信道看作一种时间可分割的信道，并将其按时间分成相等的框架，每框架的持续时间为Ts，如图2所示。每框架中包含3个阶段：频谱感知、报告和数据传输。在每框架中参与CSS且可以满足期望的感知精度的传感器最大数目用M表示。

图2 基于框架的信道结构Fig.2 Channel structure based on framework

(1)

(2)

(3)

(4)

(5)

(6)

(7)

2 问题描述

2.1 传感器的聚类

设SN表示所有传感器的集合，fk⊆SN表示可能的k个一组的传感器(即一个聚类)，它可以满足所需的检测概率和虚警概率，即有

1-(1-pf)M≤δ2〉

(8)

(8)式中：δ1和δ2分别表示最小可接受检测概率和最大可接受虚警概率。在后文中，为简单起见，fk被称为k集。 根据第2节中M的定义，k集中k的取值是1≤k≤M。对于任意给定的k，定义Ck为所有可能的k集的集合，则有

Ck={fk,1≤k≤M}

(9)

(10)

(11)

2.2 问题定义

(12)

(13)

3 启发式算法

本节提出了一种启发式算法来解决上一节定义的优化问题。在描述所提出的启发式算法之前，引入Ck的2个子集Sk(n)和Tk(n)，其中，Sk(n)表示在第n个框架开始时，Ck中能量级别要高于λth的传感器；Tk(n)表示在第n个框架开始时，处于激活状态的传感器。即有

(14)

(15)

3.1 OSSEC算法

文中提出了一种带能量约束的最佳传感器选择(optimum sensor selection with energy constraints, OSSEC)算法来解决优化问题，OSSEC算法的伪码如下：

OSSEC算法

1.n=0

4.WHILE(TRUE)

5.令P(n)=∅

7.FORk=1 toM

8.IF|Sk(n)|≥1

10.BREAK;

11.END IF

12.END FOR

13.IFP(n)=∅

14.FORk=1 toM

15.If |Tk(n)|≥1

17.BREAK;

18.END IF

19.END FOR

20.IFP(n)=∅ 无法执行CSS

21.BREAK;

22.END IF

23.END IF

24.IFP(n)≠∅

15.更新P(n)中成员的能量级别；

26.END IF

27.n=n+1;

28.END WHILE

在OSSEC算法伪码第2行中，计算所有候选组的平均检测概率；在第3行中，属于Ck(k=1,…,M)的所有候选组按照平均检测概率值的升序进行排序。然后，执行一个循环，在每框架开始时周期性地为CSS选择合适的传感器(第4至28行)。重复该循环，直到传感器的电池耗尽(20至22行)而不可能形成用于CSS的合适组为止。为了满足约束(12)式，算法搜索候选集合，其成员的能量水平大于预定阈值2。因此，我们搜索所有Sk(n)(k=1,…,M)以找到包括至少一个候选集合(第7至12行)的第一个。在找到适当的Sk(n)之后，为CSS选择具有最小平均检测概率的其中一个候选集(第9行)。如果不可能找到包含至少一个候选集合的Sk(n)，则意味着没有候选集合能够满足约束条件(12)式。在这种情况下，我们开始求解优化问题P2。从OSSEC算法的14到19行可以看出，为了求解P2，我们搜索所有的Tk(n)(k=1,…,M)，找到由至少一个候选集合组成的第一个集合。如果在这样的条件下无法找到Tk(n)，则由于传感器的电池消耗，算法停止。如果能为CSS找到适当的候选集合，则其传感器的能量水平根据其能量消耗而更新(第24行至第26行)。

(16)

(17)

(18)

(19)

4 仿真实验

4.1 实验设置和评价指标

本文采用Matlab2012进行仿真实验。在实验过程中，所选用的传感器类型是基于IEEE 802.15.4 / Zigbee[16]的Chipcon CC2420收发器。传感器被均匀地放置在半径为100 m圆形场中。FC的位置在该区域的中心。表1给出了仿真实验中使用的参数值。

表1 用于仿真的参数值

在仿真实验中，引入如下的度量标准来评估OSSEC算法的性能。设F(α)表示在αN个传感器仍处于活动状态时的网络最大生命周期，可定义为

F(α)=argmaxn{|N(n)|≥αN}

(20)

(21)

(21) 式中，F是开始时的最大框架数，有足够的即时传感器来执行CSS。设Ec表示网络存活期间CSS的总能量消耗，则有

(22)

4.2 实验结果分析

为了衡量OSSEC算法的优越性，我们将其与目前较为典型的MEESS(modified energy efficient sensor selection)算法[17]和NLISS(network lifetime improvement sensor selection)算法[18]进行了性能对比。其中，在MEESS中，传感器sj根据一个设定的函数接收参与CSS的传感器节点的优先级。sj的优先级函数如(23)式所示。

cost(j)=Δsf+Δrj-λpdj

(23)

(23) 式中，λ是pdj因子加权的乘数。在NLISS中，FC定期计算一个函数来优先考虑CSS的传感器。设pri-func(j)来表示sj的优先级函数，它可以描述为

(24)

(24) 式中：Etj表示剩余能量值；dj表示FC与sj的距离；eamp是满足FC的接收器灵敏度所需的放大率；λ,μ和εj是在每框架期间应该被更新的乘数。

图3给出了在α取不同值的情况下，不同算法中的网络最大生命周期F(α)变化情况。从图3可以看出，随着α值的增加，MEESS算法和OSSEC算法的网络生命周期都在不断下降，而NLISS算法的网络生命周期基本保持稳定不变。当α的取值在0.2～0.8时，OSSEC算法的网络最大生命周期远远长于MEESS算法和NLISS算法。然而，当α的取值在0.9和1之间时，NLISS算法的网络最大生命周期比OSSEC算法更长。这也表明了在具体应用场景中，参与CSS的传感器节点数量选择是个折中优化问题，并不是传感器节点数量越多越好，节点越多虽然可以增加CSS的可靠性，但同样会造成网络生命周期下降，应该根据设定的CSS精度来合理地选择参与CSS的节点数量，这样才能保证在满足CSS精度要求的前提下，尽可能地延长网络生命周期。

在本文研究中，信道按时间分成相等的框架。表2给出了在|P(n)|=2,3,4期间，用于OSSEC算法、MEESS算法和NLISS算法中传感器传输数据的框架百分比。从表2中可以看出，OSEEC算法中超过90%的框架是仅有2个传感器参与CSS，这样的百分比明显多于MEESS算法和NLISS算法。另一方面，OSSEC算法中3个或3个以上传感器参与CSS的框架数比其他算法要低得多。这意味着在OSSEC算法的大多数框架中，CSS是通过满足所需检测概率和虚警概率的最小数量的传感器来执行的。OSSEC算法的这种特性导致网络生命周期提高，因为传感器数量较少的候选组消耗的CSS平均能量也较少。

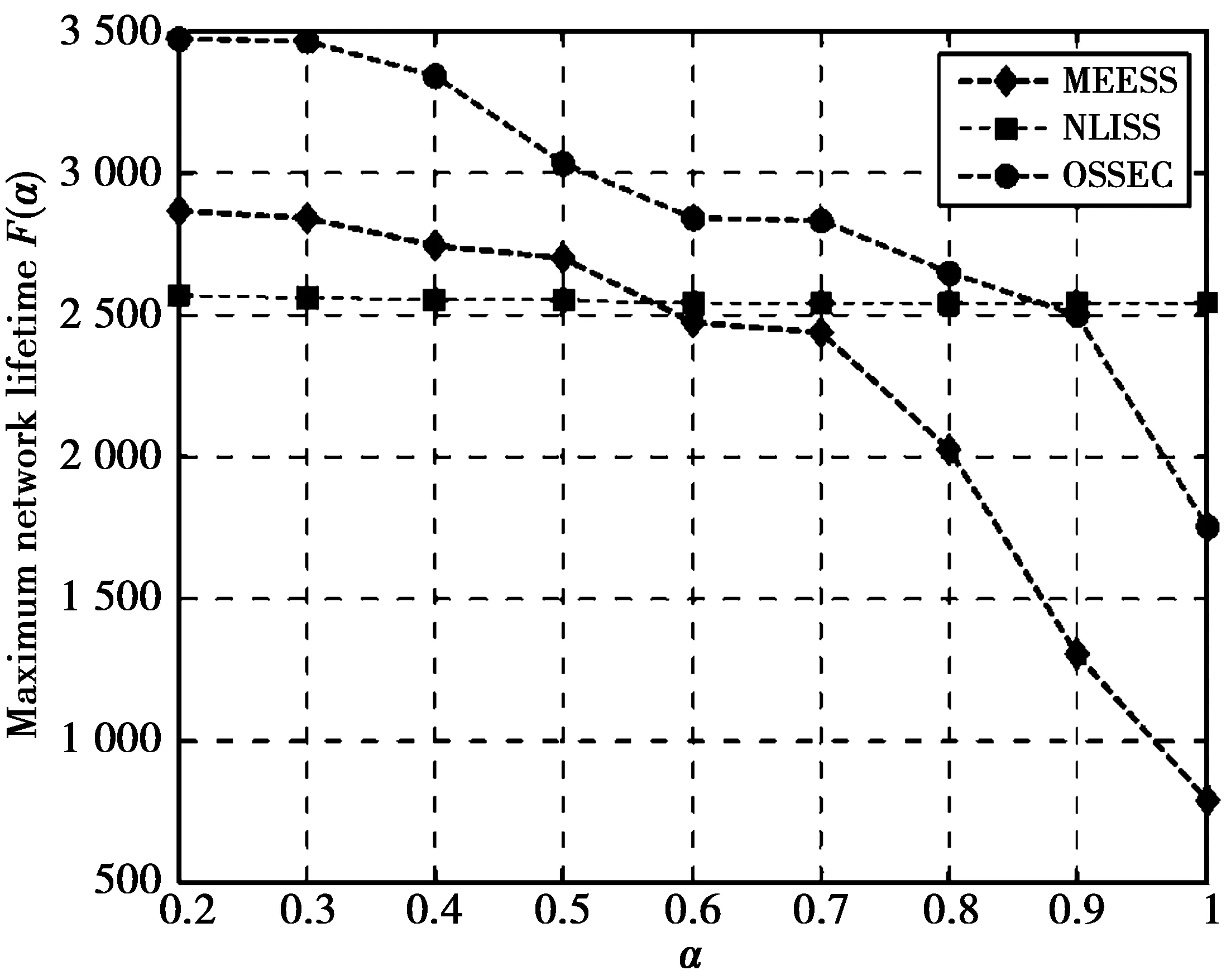
图3 不同算法中的最大网络生命周期(F(α))比较结果Fig.3 Comparison of maximum network lifetime (F(α)) in different algorithms

算法传感器传输数据框架/%|P(n)|=2|P(n)|=3|P(n)|=4OSSEC93.56.50MEESS71.5244.5NLISS53.545.80.7

图4给出了不同算法中用于CSS消耗的总能量Ec、用于将传感结果报告给FC，Erep与相对于不同传感器数量的比较结果。可以看出，随着参与CSS的传感器节点数量的增加，OSSEC算法、MEESS算法和NLISS算法的Erep基本维持不变，而3种算法的Ec都呈现出近似线性增加的趋势。但总的来看，OSSEC算法中的Ec和Erep值都要明显低于MEESS算法和NLISS算法。仔细分析其原因可知，这主要是因为，OSSEC算法通过传感器节点的聚类、根据传感器的剩余能量水平在每个框架中为CSS找到最小数量的传感器来进行数据传输等操作，减少了节点的能耗，取得了更好的性能表现。

最后，为了进一步体现本文算法的优越性，将本文提出的OSSEC算法与MEESS算法、NLISS算法在感知精度方面进行了仿真比较，实验结果如图5所示。可以看到，随着参与频谱感知的传感器节点数量的增加，3种算法的感知精度都有大的提升，但总的来说，OSSEC算法的感知精度始终要优于其他的2种算法。仔细观察曲线还可以发现，要使得感知精度达到0.9以上，OSSEC算法只需部署20个节点，而MEESS算法和NLISS算法则至少需要部署30个节点，当初始传感器节点都为10个时，OSSEC算法的感知精度也能达到0.75以上，这充分表明了OSSEC算法能够在一定程度上减弱感知性能与节点位置之间的相关性，具有较好的鲁棒性。

图4 用于CSS的能量消耗VS不同算法的传感器数量Fig.4 Energy consumption for CSS VS number of sensors in different algorithms

图5 不同算法的感知精度比较Fig.5 Comparison of perceptive accuracy of different algorithms

5 结束语

能量有效地频谱感知是认知无线电传感器网络(CRSNs)中所需研究的关键问题之一，为了提高CRSNs中主用户(PU)识别的准确性，引入了协同频谱感知技术(CSS)。目前，在实施CSS方面需要考虑的一个最具挑战性的问题是CSS的能量消耗。为此，针对具有各种检测能力的传感器所组成的CRSNs，文中提出了基于传感器选择的高能效频谱感知算法，有效节省了传感器节点的频谱感知能耗。在下一步工作中，我们研究的重点在于：①基于压缩感知理论，设计CRSNs中的异常事件检测方案；②考虑CRSNs中存在恶意节点的情况，分析频谱感知、数据安全传输与传感器节点能耗之间的关系，设计CRSNs中的恶意节点检测方法，进一步提高频谱感知的精度。