考虑执行器饱和补偿的移动机器人自适应积分滑模控制

郭一军，徐建明

(1.黄山学院 机电工程学院,安徽 黄山 245041；2.浙江工业大学 信息工程学院，杭州 310032)

0 引 言

近些年来由于移动机器人在工厂自动化、物流行业、智能家居、太空探索等领域的广泛应用，人们对其跟踪控制问题的研究引起了极大的兴趣。但由于移动机器人系统本身具有多变量、非线性和强耦合等特点，常规的控制方法很难满足其高精度的控制要求。另外，移动机器人实际控制过程中会受到系统自身参数摄动、外部环境干扰以及执行器饱和输入约束等问题的影响，尤其是执行器饱和输入约束问题不仅会影响系统的控制精度，严重时可导致系统的不稳定。因此，在设计控制器时需要补偿执行器饱和输入约束和系统不确定性因素对系统控制精度的不利影响。

当前，关于移动机器人的跟踪控制问题，常用的控制方法有反步控制法[1-3]、神经网络控制法[4-5]、滑模控制法[6-8]等。针对具有非完整约束移动机器人跟踪控制问题，文献[1-2]利用反步控制算法设计跟踪控制器，实现了移动机器人位姿跟踪误差全局一致有界。针对存在车轮打滑和外界扰动力矩影响情况下的移动机器人跟踪控制问题，文献[4]提出一种基于神经网络的跟踪控制器，保证了系统跟踪误差的全局渐近稳定。为了提高移动机器人系统的鲁棒性能及跟踪精度，文献[6]利用自适应二阶滑模控制技术设计跟踪控制器，实现了移动机器人对期望轨迹的高精度稳定跟踪，并消除了传统滑模控制中的抖振问题。以上文献虽从不同的角度实现了移动机器人的鲁棒跟踪控制，提高了系统的控制性能，但是已有研究成果多数只考虑系统内外部扰动因素对系统控制性能的影响，在设计控制器时主要考虑如何消除这些扰动对系统控制性能的不利影响，对于实际系统中存在的执行器饱和输入约束问题研究较少。

在移动机器人的实际控制过程中，执行机构的饱和问题通常是不可避免的。当控制器输出的控制信号大于执行机构所能提供的最大值时，控制饱和问题就发生了，如不进行有效处理可导致整个控制系统失稳。本文先利用双曲正切函数对执行器的饱和输入约束作近似处理，再将近似处理的误差看成系统总和扰动的一部分。从而可以通过韩京清教授提出的自抗扰控制技术，设计扩张状态观测器对系统的总和扰动加以估计和补偿。由于自抗扰控制技术对系统的总和扰动具有很好的估计性能，因此，在很多领域获得了广泛的应用[9-13]。

积分滑模在常规滑模面中加入误差变量的积分项可有效消除系统的稳态误差[14-15]，提高系统控制精度。本文结合扩张状态观测器和积分滑模控制技术各自的优势，并考虑执行器输入饱和约束问题来设计移动机器人跟踪控制器，提出了一种考虑执行器饱和补偿的移动机器人自适应积分滑模控制方法。一方面解决了系统输入饱和约束对跟踪控制性能的影响；另一方取消了普通滑模控制中对系统不确定性因素有界性的假设约束，使设计的滑模控制器更具一般性。

仿真结果表明，与固定增益的传统滑模控制方法相比，本文所提的考虑执行器饱和补偿的移动机器人自适应积分滑模控制方法不仅可使移动机器人快速稳定跟踪给定参考轨迹,而且也可有效减弱传统滑模控制中的抖振现象，有利于控制方法的实际工程应用。

1 问题描述

轮式移动机器人的运动学和动力学模型[16-17]可表示为

(1)

B(q)τ-AT(q)μ

(2)

由(1)式可得

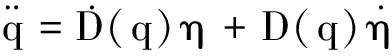
(3)

将(3)式代入(2)式中，并左乘DT可得

DTBτ-DTATμ

(4)

(5)

考虑系统执行器输入饱和约束，(5)式可重写为

(6)

(6)式中，sat(τ)=[sat(τ1)sat(τ2)]T为具有饱和约束的系统控制输入，其形式如下

(7)

(7)式中，uimax>0,uimin<0(i=1,2)为执行机构所能输出控制力矩的上下界。

采用文献[19]中的方法对饱和约束作近似处理，引入如下双曲正切函数

(8)

则sat(τi)可表示为

sat(τi)=g(τi)+d(τi)

(9)

(9)式中，d(τi)=sat(τi)-g(τi)表示饱和约束近似处理误差，且|d(τi)|满足关系

|d(τi)|≤max{uimax(1-tanh(1)),

uimin(tanh(1)-1)}

(10)

进一步由拉格朗日中值定理可得

g(τi)=g(τi0)+gξi(τi-τi0)=gξiτi

(11)

将(9)式，(11)式代入(6)式可得

(12)

2 控制器设计

由移动机器人模型(1)式、(2)式，可将系统分为速度环和位置环，需要分别设计运动学回路控制器和动力学回路控制器：①通过设计运动学回路控制器ηc，可以控制移动机器人的运动轨迹，使得其可以跟踪给定期望轨迹；②设计动力学回路控制器τ，使得(12)式中的η可以收敛于ηc。

2.1 运动学回路控制器设计

设系统的期望轨迹为

(13)

(13)式中，υr,ωr分别为移动机器人参考轨迹的线速率和角速度。

则当前移动机器人位姿相对于期望位姿的偏差在移动机器人本地坐标系中可表示为

(14)

由(1)式，(13)式，(14)式可得

(15)

依据(15)式，运动学回路控制器[19]设计为

(16)

(16)式中：β1,β2,β3>0为待设计的运动学控制器参数；υc，ωc分别为运动学回路控制器的线速度和角速度。

2.2 动力学回路控制器设计

2.2.1 扩张状态观测器设计

(17)

(18)

(18)式中，x2可看成系统的总和扰动由系统的参数摄动、饱和约束近似处理误差以及系统外部扰动等组成。在实际系统中总和扰动是不可测的，但可通过设计扩张状态观测器获得其估计值。扩张状态观测器设计为

(19)

(19)式中：e1=[e11e12]T，e2=[e21e22]T为观测误差矢量；z1，z2为扩张状态观测器的状态矢量；K1=diag{k11k12}>0,K2=diag{k21k22}>0为扩张状态观测器增益矩阵；非线性函数fal(·)的形式为

(20)

(20)式中：i=1,2；α1=0.5，α2=0.25；σ>0为待整定参数。

由文献[20-22]可知，通过选择合适的扩张状态观测器增益矩阵K1，K2，系统(19)就能很好地估计系统(18)中的状态变量，总和扰动估计误差矢量e2中的各元素有界且可收敛到原点的某一领域内，即满足关系|e21|≤l1，|e22|≤l2，其中，li(i=1,2)为正常数。

2.2.2 自适应积分滑模控制器设计

定义速度跟踪误差矢量为

e=ηc-η

(21)

为了使得系统滑动模态渐近稳定及提高系统的控制精度和鲁棒性，本文选择如下积分型滑模面

(22)

由(18)式，(21)式及(22)式可得

(23)

(24)

当系统的初始状态不在滑模面上，或系统受到不确定因素影响，那么系统状态轨迹就会偏离滑模面。所以在等效控制设计的基础上，还需要设计切换控制项τsw以保证系统状态在偏离滑模面时迫使其回到滑模面上来。因此，完整的滑模控制律可表示为

(25)

(25)式中，K3=diag{k31k32}>0为切换控制项增益矩阵，其范数需满足‖K3‖>max{l1l2}，其中，max{l1l2}为系统总和扰动估计误差上界的最大值。

由于系统估计误差的上界是未知的且难以准确获得。针对该问题，本文将结合参数自适应技术设计自适应积分滑模控制律τ为

(26)

参数自适应更新律设计为

(27)

(27)式中：ka1>0；ka2>0。

2.2.3 稳定性证明

定理1对于给定系统(12)和积分型滑模面(22)，在所设计的自适应积分滑模控制律(26)和参数自适应更新律(27)的作用下，系统速度跟踪误差将渐近收敛于零。

证取候选Lyapunov函数

(28)

对(28)式求导可得

(29)

证毕。

3 仿真研究

为了验证本文所提算法的有效性，下面将对考虑执行器饱和补偿的普通滑模控制方法和本文所提的方法进行仿真对比研究。

方法1考虑执行器饱和补偿的自适应积分滑模控制，自适应更新律参数设置为ka1=ka2=0.5。

方法2考虑执行器饱和补偿的普通滑模控制。滑模面设计同(22)式，控制律设计为

(30)

2种控制方法的控制效果如图1～图3所示，图1为跟踪误差曲线；图2为扩张状态观测器对系统总和扰动的观测误差曲线；图3为控制信号曲线，图4为方法1中参数ka1，ka2自适应变化曲线。

图1 2种方法跟踪误差曲线Fig.1 Tracking errors of two different control methods

图2 2种方法观测误差曲线Fig.2 Observation errors of two different control methods

图3 2种方法控制信号Fig.3 Control signals of two different control methods

图4 参数自适应曲线Fig.4 Parameter adaptive curve

4 结 论

本文针对执行器输入饱和约束和系统不确定性因素影响下的移动机器人跟踪控制问题，提出一种自适应积分滑模控制方法。首先，利用双曲正切函数对系统饱和约束作近似处理，并将系统方程表示为仿射函数形式；然后，设计扩张状态观测器对执行器饱和约束和不确定性因素进行补偿，在此基础上结合参数自适应技术设计系统自适应积分滑模控制器，在保证系统跟踪误差快速稳定收敛的同时，还可减弱系统抖振幅度，提高系统的稳定性和鲁棒性；最后，仿真结果验证了所提控制方法的有效性。