基于神经网络与马尔可夫链预测地表水净化装置总氮降解的效果
李金泽,叶 春,,,李春华,,罗艳丽,吕美婷,,高 悝,
(1. 新疆农业大学草业与环境科学学院,新疆乌鲁木齐 830052;2.湖泊水污染治理与生态修复技术国家工程实验室,北京 100012;3. 中国环境科学研究院,北京 100012;4.燕京理工学院建筑学院,河北廊坊 065201)
通过数学模型对预测水处理效果是当下的一个研究热点方向,而在水质预测研究中,比较常见的预测方法就是神经网络。近些年来利用神经网络预测水质方面的研究水平正在逐步提升,陆超等[1]通过一套具有三层神经网络结构的预测模型对污水处理工艺过程进行仿真验证,预测出该污水处理厂12 h后处理水质的状况,为该厂提供了一种可靠的预警处理水的方法。商巧巧[2]以水质、环境、经济效益及监督管理指标作为参考,使用改进神经网络模型对深圳市某污水处理厂运营管理进行预测和评价,使该厂在运营管理、节能减排等角度上达到最优,给污水处理厂相关管理人员提供了合理建议。宋韬略[3]利用Elman神经网络建立曝气池的预测控制模型,并对预测控制参数DO浓度和pH值进行建模预测控制,均取得满意的效果,对今后污水处理厂智能预测水质指标具有重要意义。
目前,大多数水质预测研究主要集中在污水处理及系统上,对于地表水净化装置运行的水质预测研究较少。地表水净化装置的净水过程具有非确定性、非线性、不易精确控制等特点,充分利用神经网络模糊信息处理的优势[4],可以对地表水净化效果进行装置的水净化预测。为进一步提高预测精确度,利用马尔可夫链对拟合结果及误差进行状态划分,预测分析装置的实际出水水质。
1 神经网络与马尔可夫链组合模型
1.1 BP神经网络原理
神经网络(neural network)系统是一种非线性计算处理系统[5],其特色在于信息的分布式存储和并行协同处理[6],其中BP(back propagation)神经网络使用最为广泛。它能够学习和贮存大量的输入-输出模式映射关系,并不用提供关系方程。它的学习规则[7]是使用最速下降法,通过反向传播来不断调整网络权值和阈值,使网络的误差平方和最小,具体步骤如图1所示。
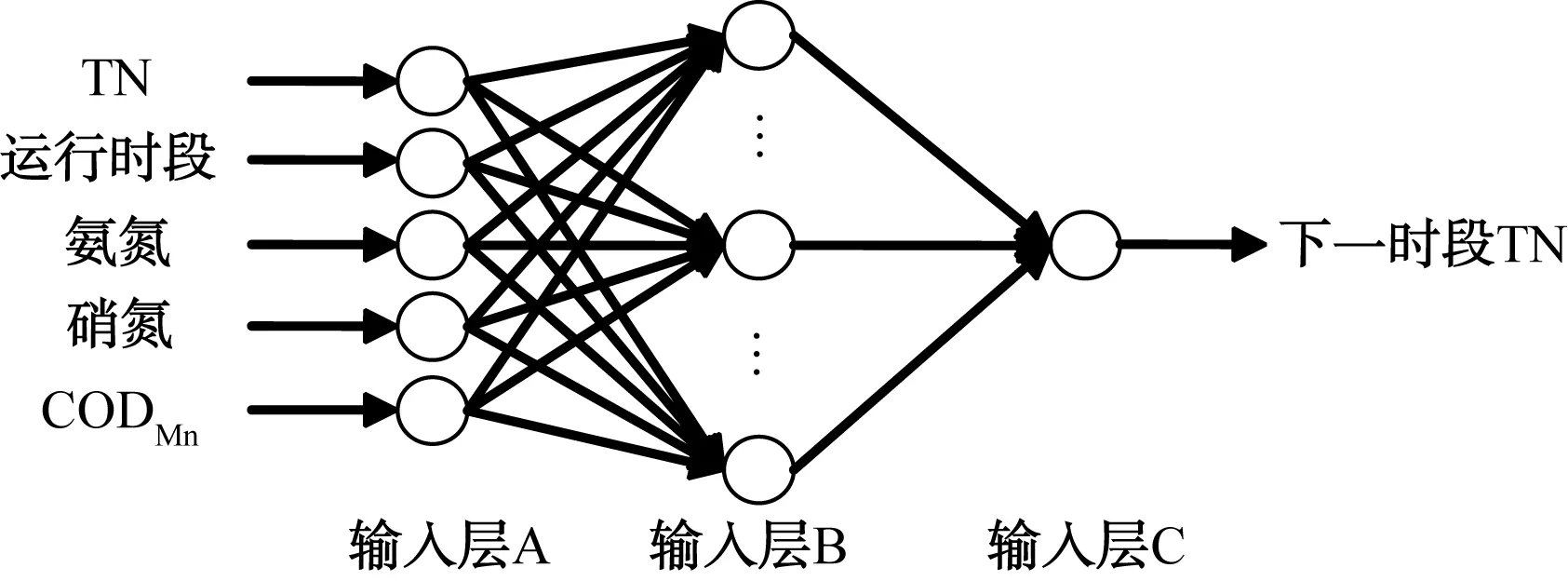
图1 BP神经网络模型结构Fig.1 BP Neural Network Model Structure
本文使用的BP神经网络结构为5输入1输出,输入层、隐含层和输出层的单元数分别为A、B和C,输入量为TN、运行时段、氨氮、硝氮、CODMn(x1,x2,...,x5),输出量为(y1),隐含层层数与节点数由实际效果决定(h1,h2,h3,...,hB)。图2为BP神经网络计算的4个基本流程。

图2 BP神经网络算法流程Fig.2 BP Neural Network Algorithm Flow
在网络训练阶段,权值和阈值的确定步骤最复杂。首先需要根据学习样本初始化权值和阈值,之后通过反向传播,不断修正输入层和隐含层、隐含层和输出层之间的权值和阈值,最后在误差满足一定要求时才会存储权值。虽然BP神经网络模型在模拟时,为保证准确性,会应用到许多样本训练和测试数据,但是这些数据受外在因素影响有时会存在一定误差,这样会导致预测结果在一定范围内随机波动,降低了预测的准确性[8]。马尔可夫链(Markov chain)的使用可以更好地消除由外在因素而产生的预测误差,因此,建立神经网络与马尔可夫链的组合预测模型,能够得到更准确的预测结果。
1.2 马尔科夫链原理
马尔可夫链是具有马尔可夫性质的随机变量的一个数列[9],通常用在排队论或其他统计学建模当中,而马尔科夫链预测法是一种适用于随机过程的科学、有效的动态预测方法[10]。该方法主要分两个过程:一是确定马尔可夫链的状态空间,二是要通过计算确定状态转移概率与状态转移矩阵[11]。
在事件发展变化过程中,在状态i的过程下一步转移到状态j的概率,简称状态转移概率,如式(1)。
pij=P{Xn+1=j|Xn=i}
(1)
其中:Pij为状态转移概率;Xn=i表示过程在时刻n处于状态i,称{0,1,2,…}为该过程的状态空间,记为S,S为状态空间的总称。对马尔科夫链,给定过去的状态X0,X1,…,Xn-1及现在的状态Xn。
通过马尔可夫链模型可以分析BP神经网络模拟预测结果误差的波动范围,并且预测波动的发展趋势,通过误差的状态转移概率矩阵对 BP 神经网络预测的结果进行进一步的精细优化。
马尔可夫链具备所谓的“无后效性”[12],即要确定该过程tn+1时刻的状态,只需知道tn时刻的情况即可,并不需要对t1,t2,…,tn-1时刻的状况完整了解。而在装置净水过程中,下一时刻水质情况只与上一个时刻有关,与之前的状态无关,故应用此预测方法对tn时刻的水质进行预测十分有效。此外,该模型的最终预测结果不是一个具体数值,而是生成一组不同概率的预测区间值,该方法可从一定程度上减少因具体数值造成的误差,提高预测准确度。
2 地表水净化装置
2.1 试验装置
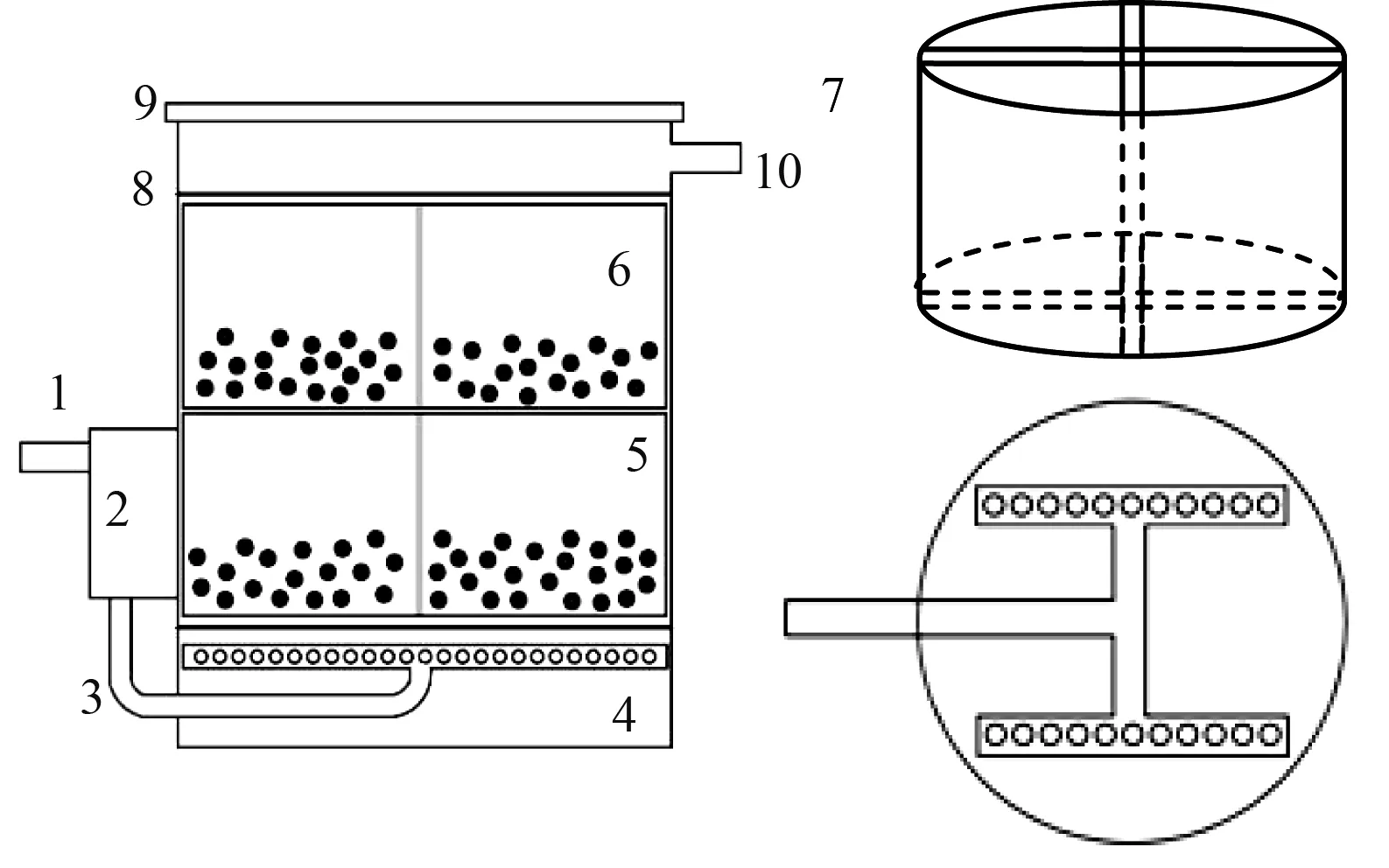
注:1-进水口;2-进水泵;3-导管;4-均布排水管;5-微生物填料微球仓;6-微生物营养补充仓;7-十字固定架;8-透水多孔板;9-桶盖;10-出水口图3 地表水净化装置平面示意图Fig.3 Schematic Diagram of Surface Water Purification Equipment
本试验装置为自主研制,共分为进水区、布水区、净水区、排水区四部分,如图3所示。净水区由微生物填料微球仓和微生物营养补充仓组成。微生物填料微球仓内为自制活性陶粒,微生物营养调节微球仓内为自制微生物营养缓释微球。该装置采用下部进水,上部出水的方式自下而上运动,泵体通电后,使填料于设备内不断旋转搅动,加快区域水循环,不仅可以增加水中溶解氧浓度,还可以通过培养土著微生物,达到水体净化的目的。
2.2 运行方案
装置运行前于微球仓装入部分自制活性陶粒,于补充仓装入部分自制微生物营养缓释微球,填料安装完毕后,拧紧上部盖子。将装置放在某大院池塘中心,固定设备于池塘底部并通电。根据池塘面积和形状,合理布设5个采样点,定期采集水样。
水样的采集主要分为装置运行前和运行后,监测指标为TN、氨氮、硝氮、CODMn等。装置运行前,采集第一次水样,装置运行后,每过3 d一次,3次后每隔7 d一次,取当天9时的水样进行水质指标检测,当场记录。此外,将每次装置运行前的水样作为原水记录。
3 装置脱氮效果模拟预测分析
3.1 基于BP神经网络的装置脱氮效果分析
通过实地监测,得到2016年10个不同时间段的某大院池塘TN、氨氮、硝氮、CODMn等指标的数据。为保证数据训练及检验的准确性,取每天某一监测指标的5个采样点的数值进行平均求解,分别作为每天这一指标的数值,其他4个指标按照同样方法求解。并以时间段从小到大为顺序,将净水时间、原水TN、氨氮、硝氮、CODMn、净化后的TN共5个指标平均值的数据进行整理,如表1所示。
调试好程序各参数后,将2016年的水质指标数据输入MATLAB软件中,以表1中序号1~8的5个采样点的平均值共8组数据进行BP神经网络训练,再将其5个采样点的值共40组数据进行辅助训练,测试9组和10组净化后的TN值的预测与实际情况,通过回归对可决系数进行求解,判定拟合优度良好,可以进行预测分析。随后,以序号1~10所有样本共60组作为训练集,对2017年5月4日~7月12日的监测数据进行模拟预测,得出出水TN的BP神经网络预测值与实际值的对比情况,结果如表2所示。
由表2可知,数据模拟误差范围为±10%,有5次模拟结果低于实际值,7次高于实际值。其中,最小误差为0.21%,最大误差为5.81%。表明出水的实际TN与预测TN误差均在一定范围内,均符合预测范围值,可应用于该装置水净化的后续水质预测中。
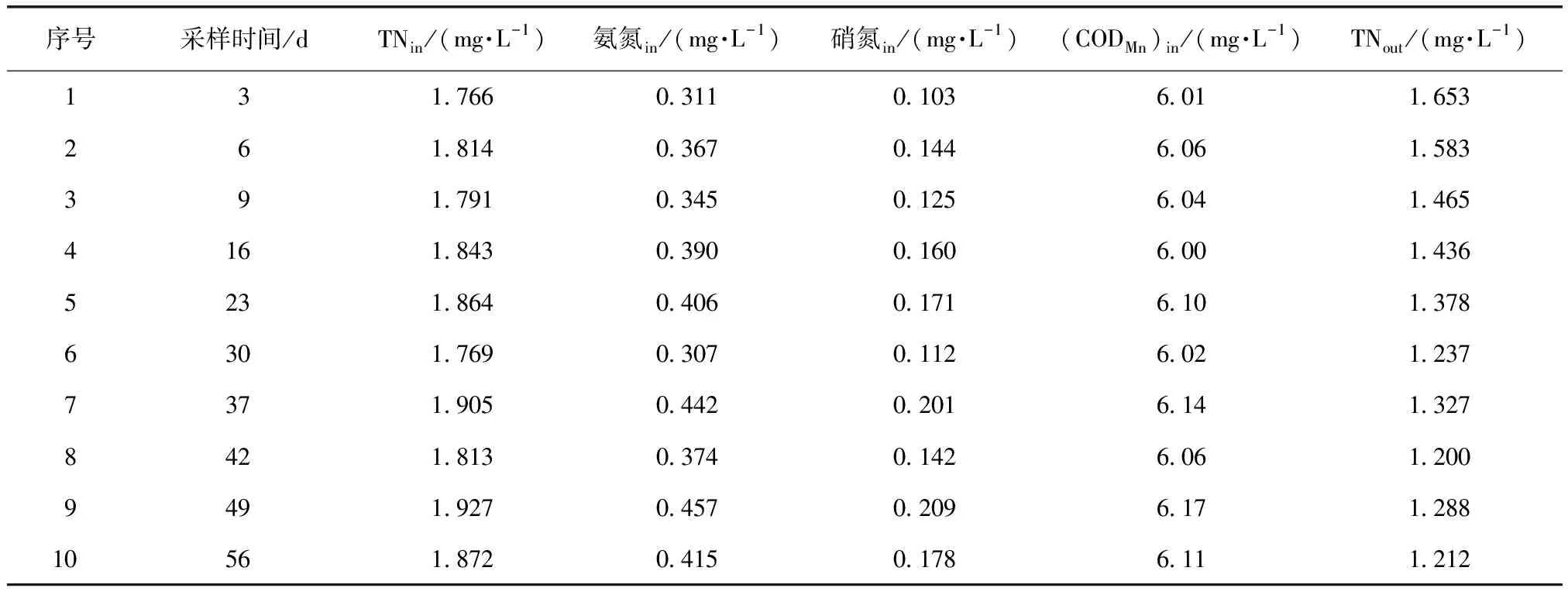
表1 市政府池塘各指标监测平均值Tab.1 Average Values of Indexes of Pond Water

表2 装置实际TN值及BP 神经网络计算拟合值Tab.2 Actual and Calculated Fitting Value of Effluent TN
3.2 基于BP神经网络的装置脱氮预测
3.2.1 马尔可夫状态区域划及转移概率矩阵
马尔科夫链的预测精度主要由转移矩阵决定,为了构造转移矩阵,首先需要合理划分误差状态区间,一般以样本减均方差的方法来确定[13]。
(2)确定转移概率矩阵。当k=1时,称pij(1)为1步转移概率,设P表示一步转移概率pij(k)所组成的矩阵,称P为系统状态的一步转移概率矩阵[14],如式(2)。
(2)
根据之前4种区域状态划分设定,表达如式(3)。
(3)
那么由状态i转向状态j的转移概率为fij≈pij/pi,(i=1,2,…,n),可得到BP模拟出水TN误差的一步转移概率矩阵,如表3所示,P的表达式可进一步表现为式(4)。
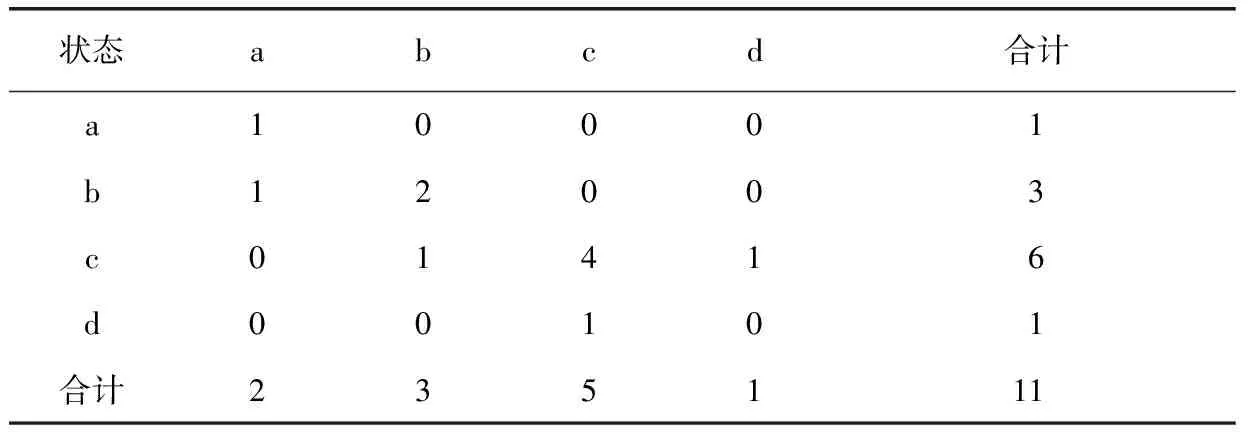
表3 装置出水水质预测结果的马尔可夫状态转移表Tab.3 Markov State Transition for BP Forecasted Results of Surface Water Quality Data

(4)
3.2.2 马尔可夫性检验及总氮预测
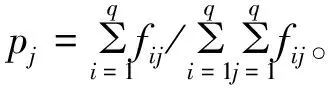

根据该装置2017年5月4日~7月12日的模拟结果,通过马尔科夫链预测模型,得到7月19日~8月16日净水后TN状态转移表,结果如表4所示。其中,参考2017年7月12日的模拟误差,初始向量为[0,0,1,0]。

表4 2017年5月4日~7月12日净水 TN 预测状态向量Tab.4 Forecasting State Vectors of TN during May 4 to July 12 in 2017

表5 2017年5月4日~7月12日净水实际值、BP拟合值与马尔可夫改进值对比情况 Tab.5 Actual, Calculated Fitting and Markov Chain Improved Value of Effluent TN during May 4 to July 12 in 2017
根据2017年7月19日~8月16日净水后总氮状态转移表改进后的最终预测结果,如表5所示。马尔可夫链改进后的预测结果并不是具体数值,而是不同概率下的范围值,符合检测结果在一定程度呈随机变化的特性,通过最大概率区间预测值可以很准确地预测实际净水水质范围。
由装置2017年7月19日~8月16日的脱氮模拟预测结果可知,出水的实际水质均符合最大概率区间内的预测范围值,表明基于BP神经网络与马尔可夫链的组合预测模型具有较高的精度,可应用于该装置净化水质的预测。
4 结论
本文所采用的组合预测模型改变了传统以往的水净化数学模型的使用,通过基于BP神经网络的预测模型,充分挖掘出数据中的变化规律与拟合趋势,可以在不掌握生物反应机理模型参数或缺乏数据的情况下进行预测。通过对该试验装置运行得到的实际数据分析计算表明,BP神经网络模型模型针对该装置具有很好的适用性,能够在一定误差范围内预测水净化后的TN范围。但是,由于该装置在净水过程存在一定波动范围的误差,故将BP 神经网络模型与马尔可夫链组合,可以恰好弥补了传统数学模型在净水过程中的不足,这为今后其它指标的预测以及多个时间段的预测提供了借鉴。

