基于小波变换的金属表面缺陷检测算法

冯国勇

（兰州资源环境职业技术学院，甘肃 兰州 730021）

小波变换的思想来自于平移与伸缩方法，是八十年代左右发展起来的一支应用数学分支[1]。小波变换在频域与时域领域内都表现出了良好的局部化性质，并且由于小波变换能够实现对高频分量使用逐步而精细的频域或时域来对步长进行取样，因而能够聚焦到观察对象的任意细节，因此小波变换被誉为数学上的显微镜[2]。而金属表面缺陷通常十分细微，因此基于小波变换的原理提出了一种新的金属表面缺陷算法。金属表面缺陷是指金属表面局部化学性质或物理性质不均匀的区域。通常情况下，金属表面缺陷是在提炼过程中产生的，包括台阶、表面空位、吸附杂质原子、位错或晶界露头、其他第二相颗粒以及非金属夹杂物等等。金属表面缺陷由于原子活性相对较高，常常会成为金属最先被腐蚀的部位。

1 设计新的金属表面缺陷检测算法

在金属提炼过程中，如果电流、电压、预热等操作不够规范，或温度设置出现失误，将影响所形成的熔池的温度、大小和形状等，造成金属表面缺陷。或者由于金属提炼不纯也容易出现金属表面缺陷。由于通过小波变换原理能够观察到观察对象的任意细节，因此在分形边缘检测方法和形态学方法的基础上结合了小波变换，提出了一种新的金属表面缺陷检测算法。利用金属缺陷区域的一些突出的特征信息，例如纹理信息、边缘信息、灰度值等，通过阈值分割或边缘提取等方法从原始图像中提取该金属的表面缺陷，其中需要利用小波变换的多尺度特性来实现大尺度下对噪声的抑制以及小尺度下对缺陷部位的精准定位从而对边缘进行可靠的识别或提取出该金属的阈值面缺陷。

当金属表面局部亮度有差异时，这种表面亮度的差异容易影响金属缺陷提取的准确程度。这时可以采取如下公式进行计算：

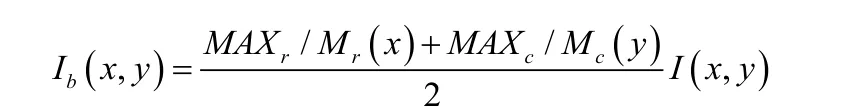
其中I为表面区域图像，Mr与Mc分别是该图像每一行以及每一列的灰度平均值，Mr与 Mc的最大值求出后分别记为MAXr与MAXc，I(x，y)是图像I上的每一个像素点，利用该公式就可以生成亮度平衡图像的相应点Ib(x，y)。

2 仿真实验

2.1 实验组

小波变换是通过分解将原始信号变成一系列小波，这些小波是由基本小波经平移和缩放之后得到的。不同于傅里叶变换，小波变换既可以通过平移基本小波获得信号的时间信息，又可以获取信号的频率信息。因此使用小波变换来进行图像增强。对这种新的金属表面缺陷检测算法设计仿真实验。在该实验种设计实验组与对比组。实验组在实验过程中，以某种稀有金属为实验对象，结合小波变换原理对图像进行增强，当缩放系数逐渐增大时，增强效果没有仍然保持平稳，没有明显减弱，仍然可以保障图像的增强效果。实验数据如表1. 图像增强效果得到保障后，可以较为轻易的捕捉到金属表面缺陷。

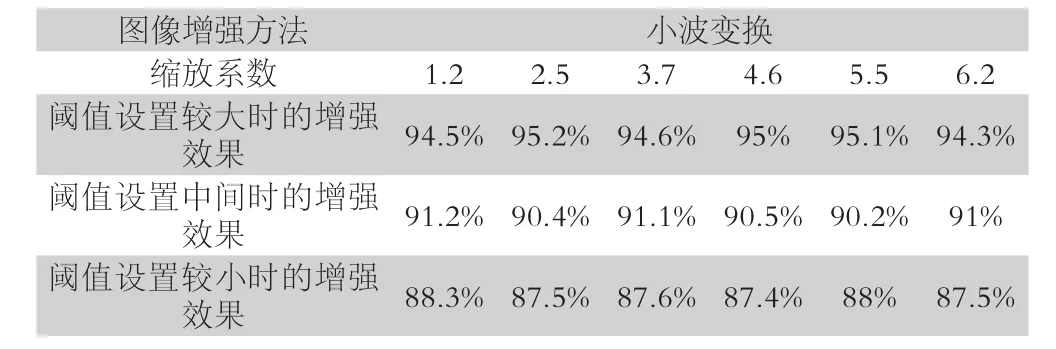
表1 实验组实验数据

2.2 对比组

对比组也同样以某种稀有金属为实验对象，采用传统基于图像处理的缺陷检测算法进行实验，在缩放系数逐渐增大时可以清晰的发现图像增强效果逐渐减弱，对图像的识别能力也逐渐减弱，无法保障图像的增强效果。因此对金属表面缺陷的捕捉越来越困难。

2.3 实验结果对比

经过实验结果的对比可以发现，结合小波变换原理设计的新的金属表面缺陷检测算法与传统基于图像处理的缺陷检测算法相比，在图像缩放系数逐渐增大时，明显可以保证图像增强效果的稳定，从而更容易捕捉到金属表面的微小缺陷。而且新的金属表面缺陷检测算法也可以保障金属表面缺陷的识别效率，区别于人工检测与传统基于图像处理的缺陷检测算法，检测速度快，结果精确客观。

人工检测标准是由人去进行主观判断，容易受到人的主观影响，不同工人即使对同样的缺陷进行判断出现的结果也不一定相同。并且人工检测的检测准确率不够稳定，人眼长期进行金属表面缺陷观察很容易就会出现视觉疲劳，从而影响对缺陷判断的准确程度。而且人工检测的效率较低，受到工人熟练程度的影响。传统基于图像处理的缺陷检测算法通常存在着参数设置过于繁杂、准确度低与速度慢等不足之处，很难满足企业在实际工业生产中进行金属表面缺陷在线检测的实际需求。

而且企业的生命就在于产品质量能够得到保障，企业占领市场的重要手段就是保证效率。当前国内外的金属制造企业在金属缺陷检测上都在追求更高的检测效率来实现生产周期的缩减，从而更迅速的占领市场，因此金属制造企业对新的金属表面缺陷检测算法有着迫切的需求。新的金属表面缺陷检测算法可以更加高效的进行金属缺陷检测，拥有良好的市场前景，并具有很大的研究意义。

3 结语

基于小波变换提出的新的金属表面缺陷检测算法经过实验对比可以发现该算法在图像增强效果方面远优于传统基于图像处理的缺陷检测算法。因此可以基于这个新的金属表面缺陷检测算法进行高效的金属表面缺陷检测，并预计有一定投入市场的价值。