复混肥料中氯离子含量测定能力验证评价研究

冷远鹏，商照聪，章明洪

(上海化工研究院有限公司 上海 200062)

氯是植物必需的16种营养元素之一，其对植物生长的主要作用包括[1- 2]：①氯作为锰的辅助因子参与水的光解反应，在缺氯的条件下，植物细胞的增殖速度变慢，叶面积减小，生长量明显下降(约减少60%)；②氯在维持细胞膨压、调节气孔运动方面具有明显作用，从而能增强植物的抗旱能力，缺氯时某些作物的气孔就无法自如开关而导致水分过多的损失；③施用含氯肥料对抑制植物病害的发生有明显作用；④作物体内氯的流动性很强，输送速度较快，能迅速进入细胞内，提高细胞的渗透压和膨压，而渗透压的提高可增强植物细胞吸水能力并提高植物细胞和组织束缚水分的能力，有利于促进植物从外界吸收更多的水分，在干旱条件下也能减少植物水分的丢失，而膨压的提高可使叶片直立、延长功能期，作物缺氯时叶片往往因失去膨压而萎蔫。

但是过量的氯离子也会产生负面影响。根系对氯离子比较敏感，在氯离子浓度达到一定范围时，会出现脱水或盐害现象(简称烧根)；另外，氯离子还会对植物根系环境造成一定破坏，如土壤板结、影响金属元素的吸收、破坏有益微生物等。因此，对氯离子的检测是肥料合格性评价中的重要指标之一，开展化肥中氯离子含量测定能力验证活动具有重要意义。

复混肥料中氯离子含量测定依据为《复混肥料中氯离子含量的测定》(GB 24890—2010)[3]，即在微酸性试样溶液中加入过量的硝酸银溶液，使氯离子转化为氯化银沉淀，然后用邻苯二甲酸二丁酯包裹沉淀，以硫酸亚铁铵为指示剂，用硫氰酸铵标准溶液滴定剩余的硝酸银，反算出样品中氯离子的含量。

1 检测实验室能力验证方法

在2016年本实验室组织的一次化肥中氯离子含量测定能力验证活动中，笔者采用Z比分数的数值作为评价实验室能力的标准。

我国检测实验室能力验证一般依据中国合格评定国家认可委员会(CNAS)发布的《能力验证结果的统计处理和能力评价指南》(以下简称《指南》)进行。《指南》定义，为了统计评价参加实验室的结果，可使用基于中位数和标准化四分位距(Standard IQR)的Z比分数[4]，Z比分数=(样品结果-中位值)/标准化IQR。中位值是一组数据的中间值，即有一半的结果高于该值，有一半的结果低于该值。四分位间距(IQR)是低四分位数值(Q1)和高四分位数值(Q3)的差值，Q1是低于结果的四分之一处的最近值，Q3是高于结果四分之三处的最近值。在大多数情况下，Q1和Q3是通过数值之间的内插法获得，则IQR=Q3-Q1。标准化IQR是一个结果变异性的量度，等于四分位间距乘以因子0.741 3，即标准化IQR=0.741 3×IQR。

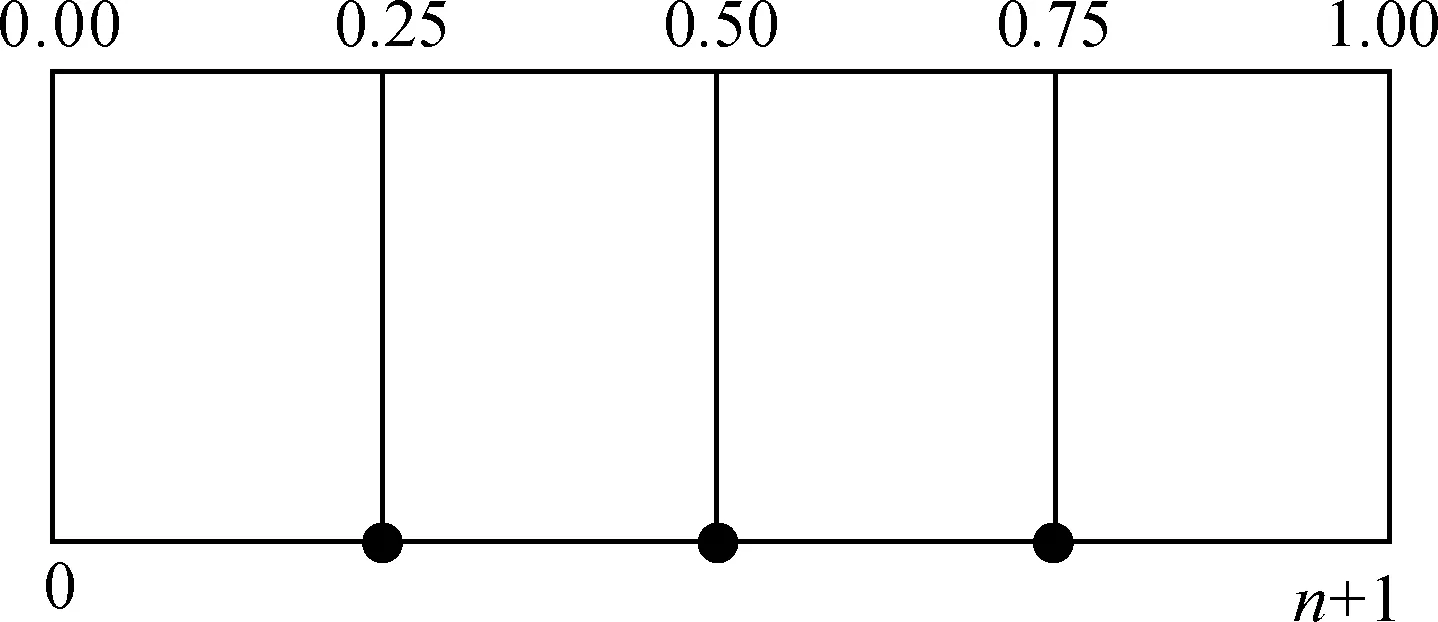
图1 四分位计算模型一

设Pi为第i四分位距对应的数值位置，按上述定义的四分位数值通常存在以下4种模型[5]。

(1) 模型一

每一位数为长度为1的方格，n个方格组合长度为n。以方格作为分割数据的载体，将n个升序排列的数装入如图1所示的方格内，则Pi=(i/4)×(n+1)，其中i=1，2，3。

(2) 模型二

如图2所示，以小球作为分割数据的依据，将n个升序排列的小球二等分，则P2=(n+1)/2；将二等分的两部分小球再分别二等分，则P1=(1+P2)/2=(n+3)/4，P3=(P2+n)/2=(3n+1)/4，表达式为Pi=1+(i/4)×(n-1)，其中i=1，2，3。

图2 四分位计算模型二

(3) 模型三

如图3所示，首先确定P2=(n+1)/2，通过P2将原数列分为2列，2列新数列不包含老数列的中间值。如果n为奇数，P2=(n+1)/2为整数，应舍弃，新数列由1到P2-1及P2+1到n组成，相应的P1=(1+P2-1)/2=(n+1)/4，P3=(P2+1+n)/2=(3n+3)/4；如果n为偶数，P2=(n+1))/2为分数，自然不存在于2列新数列中，新数列由1到n/2及(n/2)+1到n组成，相应的P1=(1+n/2)/2=(n+2)/4，P3=(n/2+1+n)/2=(3n+2)/4。

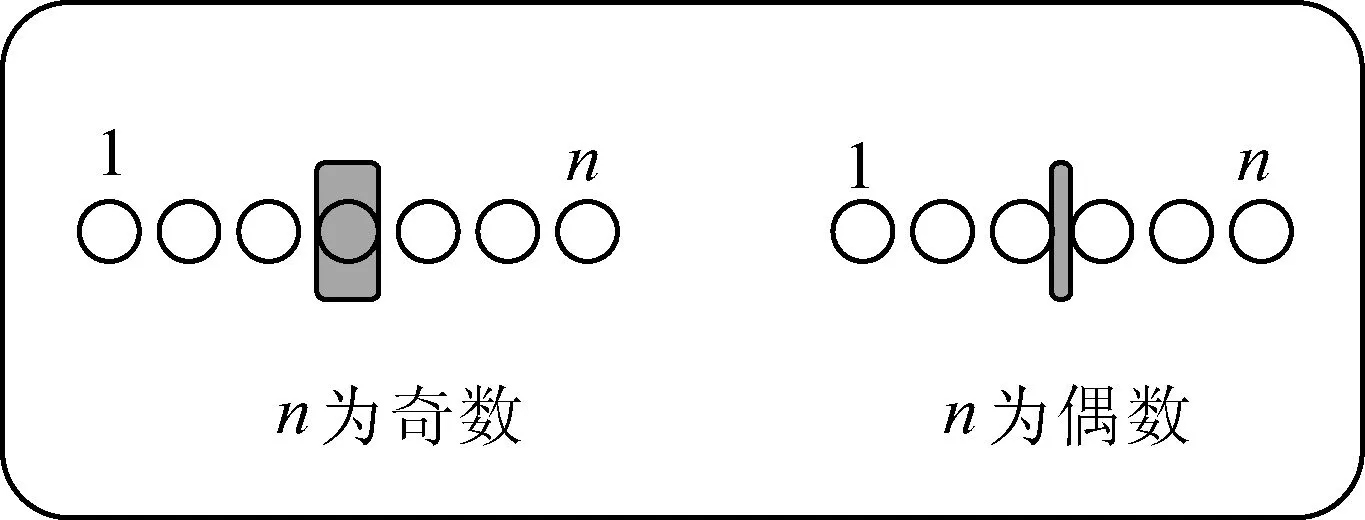
图3 四分位计算模型三

(4) 模型四

如图4所示，首先确定P2=(n+1)/2，通过P2将原数列分为2列，2列新数列都包含老数列的中间值。若n为奇数，P2=(n+1)/2，新数列由1到P2及P2到n组成，相应的P1=(1+P2)/2=(n+3)/4，P3=(P2+n)/2=(3n+1)/4，与模型二相同；若n为偶数，P2=(n+1)/2，新数列由1到n/2及(n/2)+1到n组成，相应的P1=(1+n/2)/2=(n+2)/4，P3=(n/2+1+n)/2=(3n+2)/4，与模型三相同。

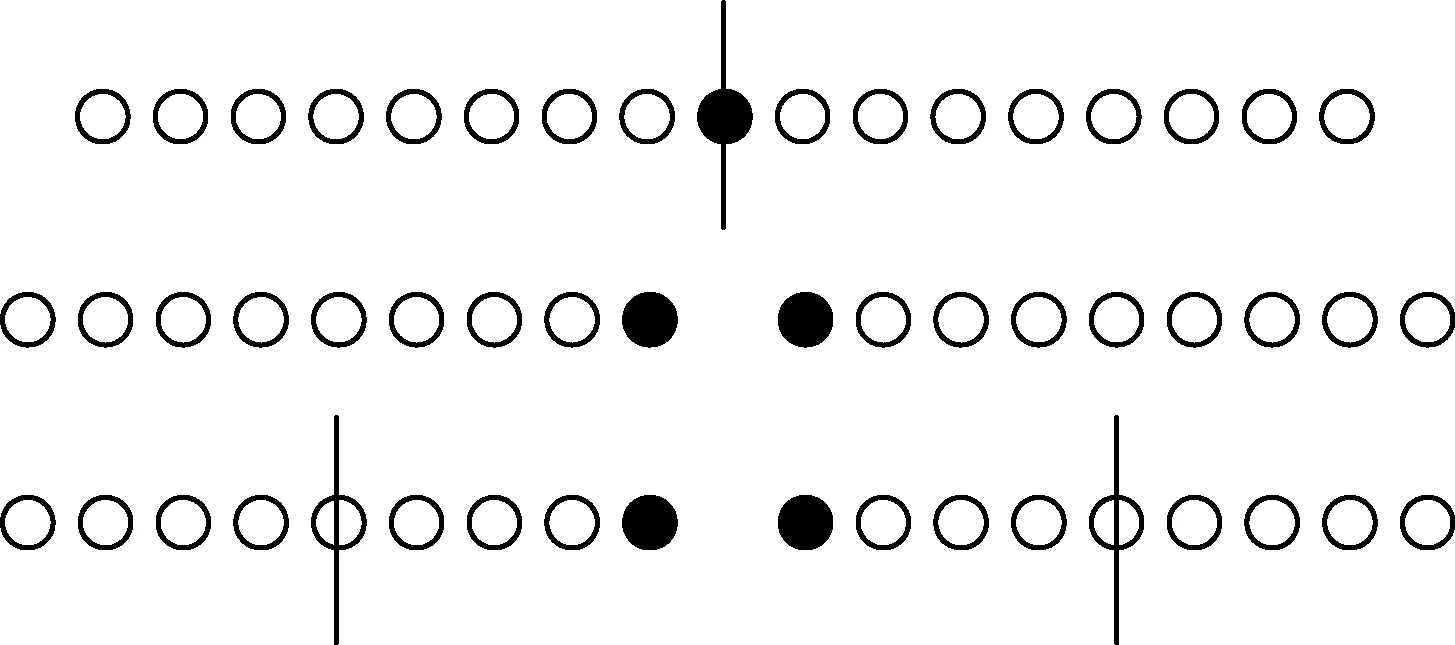
图4 四分位计算模型四

这4种模型覆盖了目前我国能力验证结果处理方法[6- 10]中常见的统计模型，其各自的特点如表1所示。

表1 四分位计算模型特点

模型P1n为奇数n为偶数P2P3n为奇数n为偶数一(n+1)/4(n+1)/2(3n+3)/4二(n+3)/4(n+1)/2(3n+1)/4三(n+1)/4(n+2)/4(n+1)/2(3n+3)/4(3n+2)/4四(n+3)/4(n+2)/4(n+1)/2(3n+1)/4(3n+2)/4

2 主要试剂和材料

主要试剂：邻苯二甲酸二丁酯，分析纯；1+1硝酸溶液，由浓硝酸(分析纯)与三级水按1∶1配制；0.05 mol/L硝酸银溶液，称取8.7 g硝酸银(分析纯)并溶于水中，稀释至1 000 mL，储存于棕色瓶中；1 mg/mL氯离子标准溶液，准确称取1.648 7 g事先在270～300 ℃下烘干至质量恒定的基准氯化钠(基准试剂)于烧杯中，用水溶解后转移至1 000 mL量瓶内，稀释至刻度，混匀，储存于塑料瓶中；80 g/L硫酸亚铁铵指示剂，将8.0 g硫酸亚铁铵(分析纯)溶解于75 mL水中，过滤，加几滴硫酸使棕色消失后再稀释至100 mL；0.05 mol/L 硫氰酸铵标准滴定溶液，称取3.8 g硫氰酸铵(分析纯)溶解于水中，稀释至1 000 mL。

主要材料：250 mL烧杯，250 mL容量瓶，25.0 mL 移液管，250 mL锥形瓶，50 mL通用滴定管。

3 分析步骤及计算方法

称取1～10 g(精确至0.000 1 g)试样于250 mL 烧杯中，加入100 mL去离子水，缓慢加热至沸并保持微沸10 min，然后冷却至室温，将溶液转移至250 mL容量瓶中，稀释至刻度，混匀，干过滤，弃去最初部分的滤液；吸取含氯离子25 mg左右的滤液于250 mL锥形瓶中，加入5 mL 硝酸溶液和25 mL硝酸银溶液，摇动至沉淀分层，然后加入5 mL邻苯二甲酸二丁酯，摇动片刻；加水使溶液总体积为100 mL，加入2 mL硫酸亚铁铵指示剂，用硫氰酸铵标准溶液滴定剩余的硝酸银至出现浅橙红色或浅砖红色为止，同时进行空白试验。

氯离子质量分数w(Cl-)按下式进行计算：

式中：V0、V1——分别为空白和滴定试样消耗的硫氰酸铵标准溶液的体积，mL；

c——硫氰酸铵物质的量浓度，mol/L；

0.035 45——氯离子毫摩尔质量，g/mmol；

m——试样质量，g；

V分、V总——分别为滴定分取体积和试样总定容体积，mL。

4 试验结果及数据统计

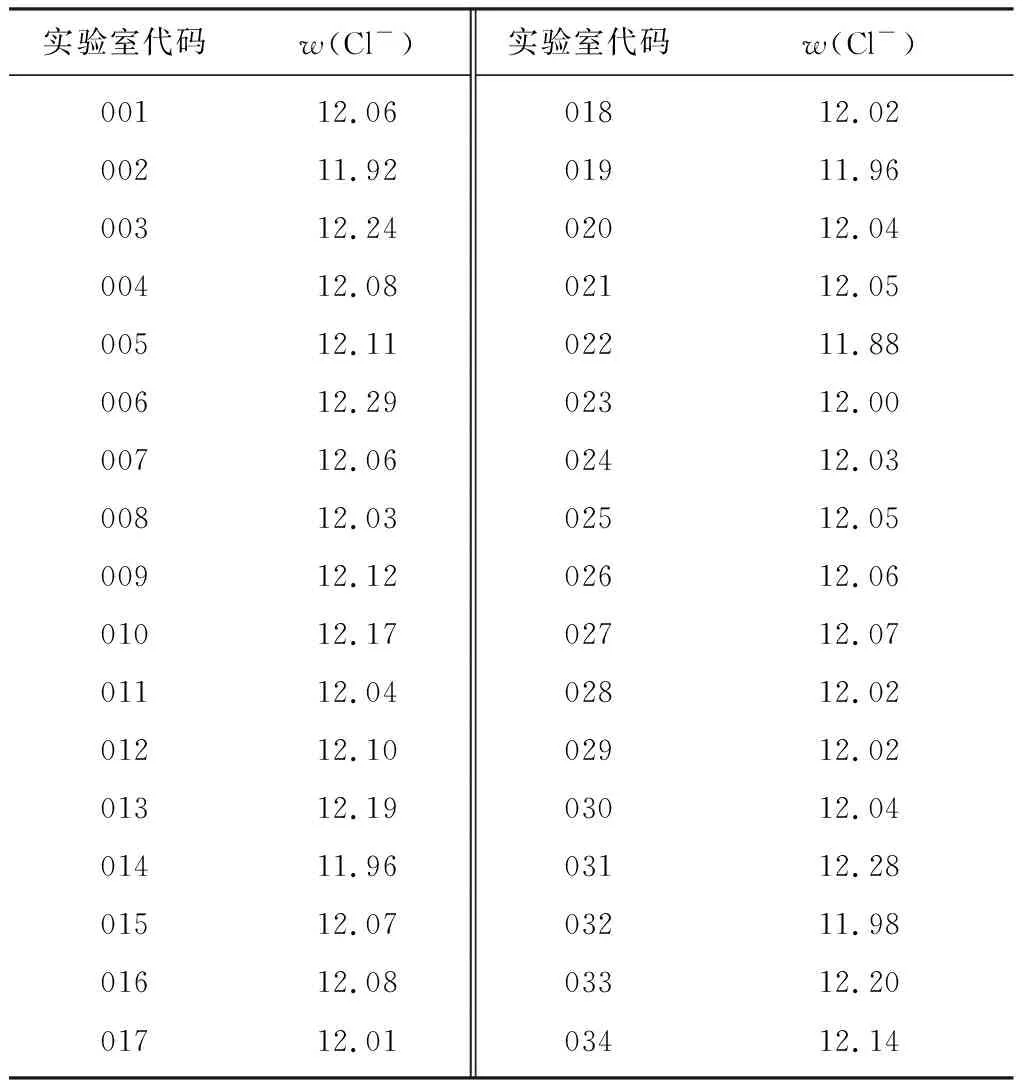
氯离子含量测定能力验证活动由复混肥料全国联动抽查承检机构共34家实验室报名参加，所测样品均为同一复混肥料，样品的均匀性及稳定性已通过本实验室验证。34家实验室全部按要求反馈了测定结果，如表2所示。

表2 实验室反馈的测定结果 %

利用不同四分位计算模型分别处理统计结果，统计过程如表3和表4所示，其中|Z|≥3为不满意结果(离群值)，2<|Z|<3为可疑结果，|Z|≤2为满意结果。

如表5所示，由于不同模型的计算公式差别，导致002实验室和013实验室的能力评价结果不尽相同，即采用模型一的能力评价结果均为满意，而采用模型二、三和四的实验室能力评价结果均为可疑。

表3 不同四分位计算模型统计标准化IQR

模型P1Q1P2Q2P3Q3标准化IQR一8.7512.02017.5012.05526.2512.1120.068 57二9.2512.02017.5012.05525.7512.1080.064 86三9.0012.02017.5012.05526.0012.1100.066 72四9.0012.02017.5012.05526.0012.1100.066 72

表4 不同四分位计算模型统计实验室反馈结果的Z值

表5 不同四分位计算模型对002实验室和013实验室的能力评价结果

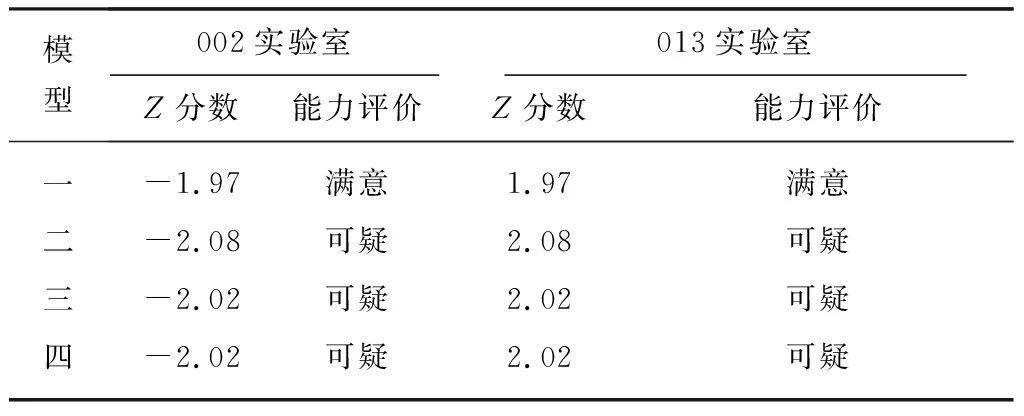
模型002实验室013实验室Z分数能力评价Z分数能力评价一-1.97满意1.97满意二-2.08可疑2.08可疑三-2.02可疑2.02可疑四-2.02可疑2.02可疑

5 模型讨论

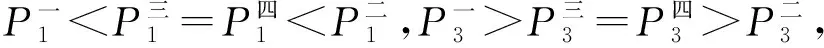
表6 四分位计算模型特点

模型P3-P1n为奇数n为偶数一(n+1)/2二(n-1)/2三(n+1)/2n/2四(n-1)/2n/2

图5更直观地示意了不同四分位计算模型对IQR结果的影响，柱越长代表IQR值越大，即相应的|Z|越小。

图5 不同四分位计算模型对IQR结果的影响

分析各模型发现：模型一以方格作为分割数据的载体，最大数位置为n+1，比实际最大数位置增加了1位，这是该模型明显的缺陷；模型二以小球作为分割数据的依据，在第2次分割时完全保留构造出的P2；模型三完全舍弃了构造出的P2；模型四则在n为奇数且P2存在时保留P2，在n为偶数且P2不存在时以n/2代替P2作为分割依据，但是此种处理方式在第2次分割求解P1和P3过程中使用了完全不同的中分位值，是否合理并无公论。

6 结语

综上所述，以4种分位距模型评价了复混肥料中氯离子含量测定能力验证活动中各参与实验室的能力，使用模型一，002实验室和013实验室的能力评价结果均为满意；使用模型二、模型三和模型四，002实验室和013实验室的能力评价结果均为可疑。进一步理论分析了不同的计算模型导致能力验证评价结果出现差异的统计学原因，证明模型一最易使评价结果偏满意，而模型二最易使评价结果偏可疑或不满意。

在实际能力验证活动中，模型一和模型二的应用较为常见。模型一对实验室评价较温和，而模型二最严厉。在数据处理工作量上，模型二可利用EXCEL中的QUARTILE函数直接运算得到结果，过程较为简便。