利用俯视图确定小立方体的个数

◎储建国

（作者单位：江苏省常州市武进区前黄实验学校）

我们在研究几何体视图问题时，经常会遇到已知几何体的主视图和俯视图，确定搭成几何体的小立方体的个数最多和最少的问题.对于这类问题，同学们普遍感到困难.下面介绍一种比较简便易行的解题策略，供同学们参考.

我们可以根据主视图，在俯视图上的每一个小正方形上标出每一个小正方形所在处可能摆放小立方体的数目，再把这些数按照所给要求相加，从而计算出搭成几何体所需立方体的个数.具体方法如下：

第一步：根据主视图数出每列中的小正方形个数，在俯视图对应的列（从左到右的顺序）的第一行（从上到下的顺序）的每一个小正方形内填入相应的数字；

第二步：在俯视图对应的列的其他行的小正方形内填入不超过第一行且不低于1的整数；

第三步：若要求的是最多需要小正方体的个数，则应取俯视图中每一个小正方形上最大的数字（若相同，则任取一个），再把它们相加，即可得最多小正方体的个数；若要求的是最少需要小正方体的个数，则应取俯视图中每一个小正方形上最小的数字（若相同，则任取一个），再把它们相加，即可得最少小正方体的个数.

例1如图1，是由一些相同的小正方形构成的立体图形的三种视图.构成这个立体图形的小正方体的个数是（ ）.

A.4 B.5 C.7 D.8

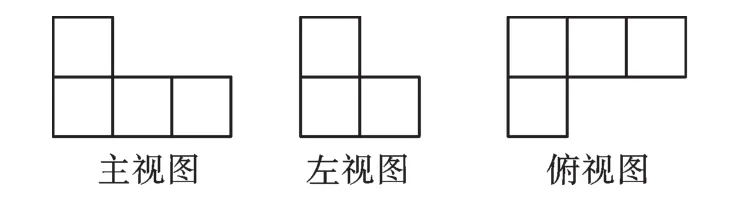
图1

【思路分析】由主视图可知：

（1）俯视图最左边有两层高，因此俯视图最左边两格都可能有2层，至少是1层，两个至少有一个是2层；

（2）俯视图右边两格肯定一层高.每一格可能层数如图2所示.

图3

图2

图4

由左视图可知：俯视图最下面一个肯定一层，上面3格可能1层或2层，但至少1层，且至少有一个为2层.每一格可能层数如图3所示.

综合图2、图3可知，各格小立方体数如图4所示，因此小正方体的个数是5个.

【点评】可以将由主视图、左视图得到的信息标在俯视图中，综合处理这些信息得出俯视图每个方格中立方体的个数，从而求出总共有多少个小正方体.

例2一个几何体是由若干个相同的正方体组成的，其主视图和左视图如图5所示，则这个几何体最多可由多少个这样的正方体组成？（ ）

A.12个 B.13个 C.14个 D.18个

【分析】由主视图和左视图宽度可知，该几何体的俯视图应该在如图6所示3×3的范围内.

图6

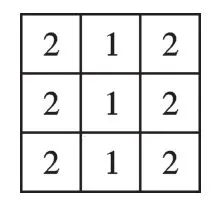
图7

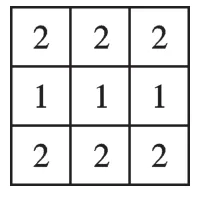
图8

图9

由于主视图两旁两列有两层小方格，中间一列1层小立方体，因此俯视图区域内每个方格内小正方体最多个数如图7所示.

由左视图信息，可知俯视图区域内每个方格内小正方体最多个数如图8所示.

综合图8、图9信息可知俯视图区域内每个方格内小正方体最多个数如图9所示.

【点评】本题没有俯视图，借助主视图的宽与俯视图的宽相等，左视图的宽与俯视图的高相等，将俯视图限制在一个3×3的方格内，然后在俯视图的方格内标出可能的数字，求出这个几何体中小正方体的个数.

当然，求搭成这样几何体的小立方体的个数的方法还很多，同学们在以后的学习中要多注意留心总结，争取找到最简洁的解题方案.