浅谈ANSYS计算四边支承玻璃

邱 科

（南京广博装饰股份有限公司 江苏南京 210000）

玻璃幕墙是当代的一种新型墙体，它赋予建筑的最大特点是将建筑美学、建筑功能、建筑节能和建筑结构等因素有机地统一起来，配合光照等使建筑物与自然融为一体。玻璃幕墙，顾名思义，是面板材料为玻璃的建筑幕墙。作为直接承受风荷载的构件，面板的计算至关重要，而采用规范公式计算仅应用于受均布荷载的四边支承和对边支承的情况，十分有限。此时，有限元计算便显得十分重要。

我们分别选用尺寸为 1.5m×1.5m、1.5m×3.0m、1.5m×4.5m、1.5m×6m的8mm（TP）+12A+8mm（TP）的中空玻璃（注：此处玻璃配置仅用于研究计算，并不一定满足安全玻璃的最大使用面积的要求），风荷载标准值取WK=2.0kN/m2，抗震设防烈度取Ⅷ度（0.10g），αmax=0.8。

1 荷载计算

刚度计算时：

荷载标准值为：SK=WK=2.0kN/m2；

强度计算时：

作用于中空玻璃上的风荷载标准值分配到单片玻璃上：

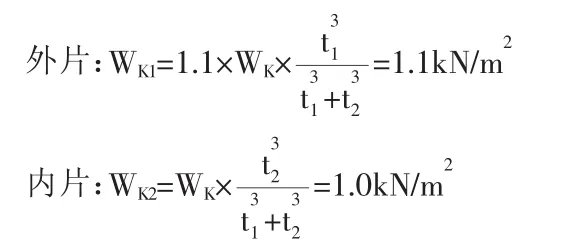
因外片所受荷载较大，仅验算外片强度即可：

外片玻璃的自重荷载标准值为：GK=8×25.6=0.205kN/m2；

外片玻璃的水平地震作用标准值为：qEK=βEαmaxGK=5×0.08×0.205=0.082kN/m2；

荷载设计值为：S=ψWγWWK1+ψEγEqEK=1.4×1.0×1.1+1.3×0.5×0.082=1.593kN/m2。

2 按规范公式计算的结果

（1）1.5m×1.5m 玻璃

变形：6.99mm；强度：13.73MPa。

（2）1.5m×3.0m 玻璃

变形：17.44mm；强度：31.06MPa。

（3）1.5m×4.5m 玻璃

变形：20.99mm；强度：36.56MPa。

（4）1.5m×6.0m 玻璃

变形：22.07mm；强度：38.21MPa。

目前国内涉及玻璃强度、挠度计算的规范或标准有《玻璃幕墙工程技术规范》（JGJ102-2003）、《建筑玻璃应用技术规程》（JGJ113-2015）、《上海市建筑幕墙工程技术规范》（DGJ108-56-2012）。以上数据为根据《玻璃幕墙工程技术规范》（JGJ102-2003）计算的结果，由大量的实验加推导并乘了很多的经验系数所得。

3 按ANSYS计算的结果

将玻璃面板的四条边编号如下：

图1

情况一：四边铰接，即四边都约束x、y、z三个方向的平动约束（按小变形理论）：

（1）1.5m×1.5m 玻璃

变形：7.496mm；强度：20.9MPa。

（2）1.5m×3.0m 玻璃

变形：18.66mm；强度：29.8MPa。

（3）1.5m×4.5m 玻璃

变形：22.515mm；强度：35.8MPa。

（4）1.5m×6.0m 玻璃

变形：23.585mm；强度：37.7MPa。

情况二：四边铰接，即四边都约束x、y、z三个方向的平动约束（按大变形理论）：

（1）1.5m×1.5m 玻璃

变形：5.275mm；强度：13.2MPa。

（2）1.5m×3.0m 玻璃

变形：7.809mm；强度：13.6MPa。

（3）1.5m×4.5m 玻璃

变形：7.858mm；强度：13.7MPa。

（4）1.5m×6.0m 玻璃

变形：7.855mm；强度：13.8MPa。

由于玻璃厚度t远小于长度和宽度，应用薄板理论进行计算。根据理论，板发生弯曲变形时如果挠度与厚度之比小于或等于1/5，可认为属于小挠度问题，若超过这个限值，则可归属于大挠度问题。研究发现，当玻璃的变形小于自身厚度时，可采取小变形理论进行计算；但当玻璃的变形大于自身厚度时，需要考虑力随着物体变形而重新分布的几何非线性，此时小变形理论不再适用，应采取大变形理论进行计算。

从上面的结果可以看出，按大变形理论计算时，玻璃的长宽比越大，ANSYS计算结果比规范计算结果小越多，差值越明显。这时候，我们就要思考模型本身的正确性，是否要改变计算时的边界约束条件，使之更符合实际情况。现修改玻璃的边界条件为

情况三：四边抗风约束，第4边两点承重，第1边两点侧向约束

（1）1.5m×1.5m 玻璃

变形：6.833mm；强度：19.1MPa。

图2

图3

（2）1.5m×3.0m 玻璃

变形：15.955mm；强度：27.9MPa。

图4

图5

（3）1.5m×4.5m 玻璃

变形：21.261mm；强度：32.4MPa。

图6

图7

（4）1.5m×6.0m 玻璃

变形：23.562mm；强度：37.5MPa。

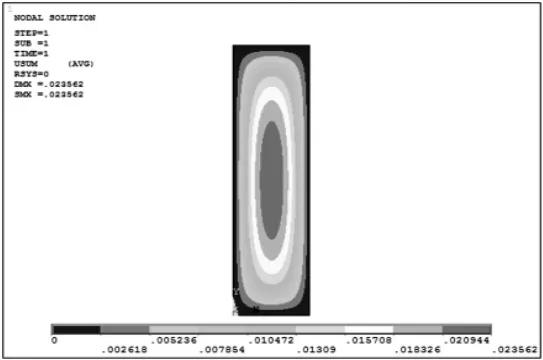
图8

图9

上述计算结果对比说明，当长宽比大于1时，采用ANSYS有限元计算的变形值和应力值与规范计算结果比较接近，可以认为计算模型合理正确；当长宽比接近1时，应力结果偏大，存在误差。按大变形理论进行计算时，四边抗风、第4边两点承重、第1边两点侧向约束模型的计算结果不敢说能适用于所有长宽比计算，是完全准确的，但却是比较接近实际情况的。

4 结论

采用有限元计算时，情况三的边界约束条件更符合实际，计算模型合理、可行。