废旧钻杆叠合梁受力性能研究
赵雪芹 古 松,2 王新龙
(1.西南科技大学土木工程与建筑学院 四川绵阳 621000;2.长安大学旧桥检测与加固技术交通行业重点实验室 陕西西安 710061)
目前废旧钻杆应用形式多为钻杆平铺在桥墩上,横向进行简单焊接。此种结构形式简单,钻杆截面刚度小,使用跨径多为2~3 m,当重型机械设备经过时,桥梁挠度较大且端部钻杆上翘明显,车辆行驶安全性和舒适性差,不满足实际工程需要,需要对新型的废旧钻杆结构形式进行研究,提高其使用跨径,以更好地应用于短跨桥涵工程中。
叠合梁结构是建筑结构中常见的一种预制构件,具有施工简便、工期短、造价低廉、整体性强等优点。目前,国内外对叠合梁的研究大都集中于混凝土材料中。结合叠合梁结构的特点和研究现状,文章以截面抗弯刚度较大的“品”字形钻杆叠合梁为研究对象,通过理论分析和叠合单梁室内试验,对其规范允许的最大承载力以及抱箍约束效果进行研究。
1 废旧钻杆叠合梁构造设计
文献[1]指出,提高单梁截面刚度对整体钻杆桥的挠度减小最有效。“品”字形叠合梁,显著增大了钻杆单梁的截面刚度,但在荷载作用下叠合梁会发生弯曲变形,钻杆之间产生相对滑移,荷载较大时,下部钻杆还会产生横向位移,导致截面形状改变,影响叠合梁整体性,减小其承载力。为减小这些因素的影响,在叠合梁中部设置抱箍,如图1所示。抱箍和钻杆之间设置5 mm厚橡胶垫,增大两者局部摩擦力,提高整体性,构成本文研究的废旧钻杆叠合梁(图2)。此种结构形式叠合梁发生弯曲变形时,理论上抱箍可以很好地限制下部两根钻杆的横向分离,保持其截面形状基本不变,抱箍作用处产生的局部较大摩擦力对限制钻杆之间的相对滑移有一定的作用,可以提高承载力。
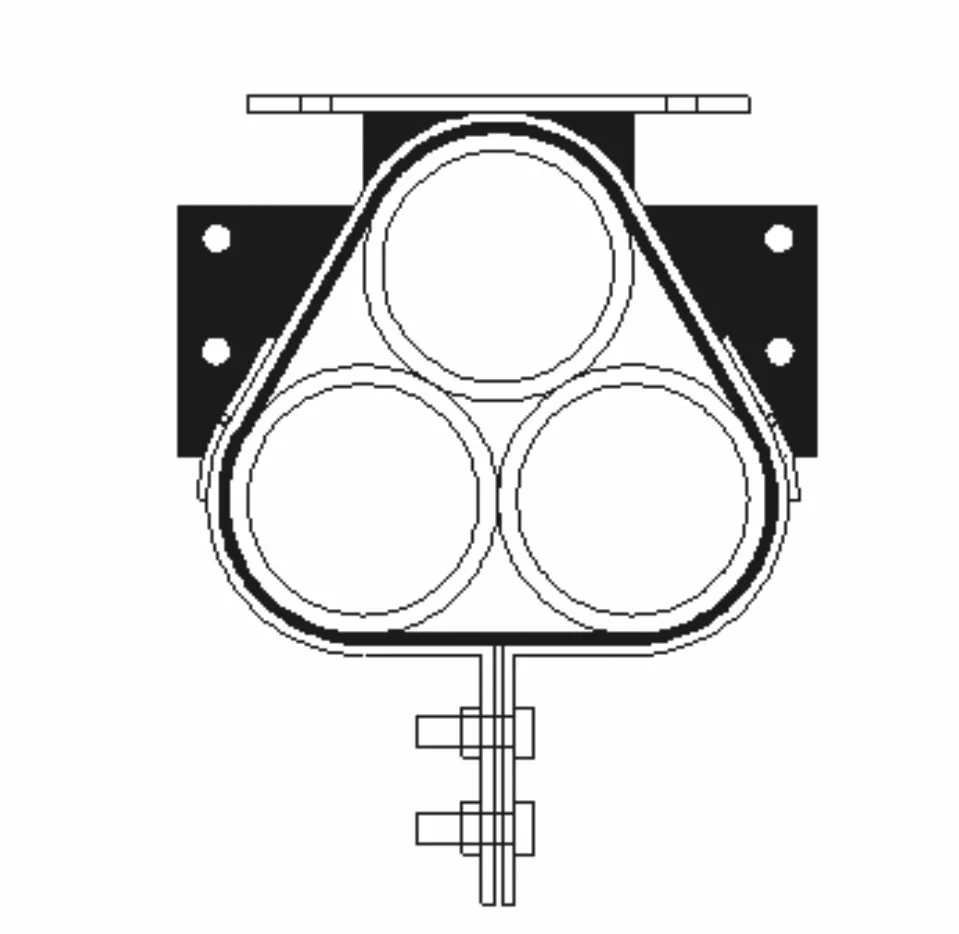
图1 抱箍横截面Fig.1 The cross section of the hoop

图2 废旧钻杆叠合梁Fig.2 The composite beam of waste drill pipes
2 组合梁挠度计算理论
国内外常用组合梁形式为钢-混凝土组合梁,它充分利用了混凝土抗压及钢梁的抗弯拉特性,在建筑和桥梁结构中得到广泛应用。
2.1 钢-混凝土组合梁挠度计算方法
目前已有大量针对钢-混凝土组合梁挠度计算方法的理论和试验,挠度计算方法主要有换算截面法、折减刚度法、解析法。
(1)换算截面法。将钢材和混凝土材料组成的实际截面按照它们弹模的比例关系进行换算,形成一种匀质截面后开展计算。该法概念清晰、使用简单,我国原GBJ 17—1988《钢结构设计规范》便是采用此方法。
(2)折减刚度法。聂建国[2]等考虑不同材料的组合梁发生弯曲变形时界面的相对滑移效应,建立了微分方程,通过推导,得出了不同荷载作用下组合梁由于相对滑移效应导致的变形的理论计算公式,进一步进行简化以及修正,最终提出组合梁位移计算的折减刚度法。我国目前的GB 50017—2003《钢结构设计规范》便采用了该方法。
(3)解析法。蒋丽忠和余志武等[3]开展了集中荷载及均布荷载作用对组合梁的变形影响及滑移的研究,最终得出组合梁的挠度和滑移计算解析式。
以上3种方法有各自的优缺点。换算截面法概念清晰,使用简单方便,但忽略了组合梁材料接触面之间的滑移效应,导致截面抗弯换算刚度偏高,使得计算的挠度小于实际值,偏不安全。聂建国等提出的组合梁挠度计算的折减刚度法概念清晰,便于工程师对其掌握和应用,然而,徐荣桥等[4]研究发现此法存在随着抗剪连接程度增大截面抗弯刚度反而减小的情况。解析法计算准确,但公式极为复杂,不便于推广应用。因此需要一种简单、精确的组合梁挠度计算方法。
2.2 有效刚度法
周东华[5]等针对聂建国提出的折减刚度法适用范围有限、精确度不高的缺陷,结合Wang[6]的以抗剪切连接件刚度为基础的计算方法,提出了组合梁挠度计算的有效刚度法。上、下层梁轴向刚度是否发挥作用是此方法的核心。受力特点可以用两弹簧的联接模型形象表示,如图3所示。
无剪切连接时,两弹簧之间是断开的,上下截面相对自由移动,刚性连接时,两弹簧串联在一起,叠合梁是一个完全整体结构,此时,上、下截面的轴力达到最大值。弹性剪切连接时,在k1和k2之间又串联了1个弹簧k3,k3为中部所有弹性剪切件的折减刚度。

图3 3种剪切连接的弹簧力学模型Fig.3 Spring model for three types of connections
3个弹簧串联后的刚度为:
(1)
式中EAeff为组合梁的有效轴向刚度,EcAc,EsAs分别为上、下层梁的轴向刚度。k3越大,EAeff越大,反之EAeff越小。利用公式(1)得到截面的有效轴向刚度EAeff,通过公式(2)确定组合系数β和全截面的有效抗弯刚度EIeff,继而计算组合梁挠度。
(2)
式中d为上下层梁中性层之间的垂直距离,EI为无剪切连接时截面的抗弯刚度。
当界面之间有多个弹性剪切连接件作用时,因为滑移是不均匀的,滑移大的地方连接件发挥的作用大,反之小,所以要对连接件的剪切刚度进行折减得到k3。曹兴贵[7]等对弹性剪切件的布置和折减强度进行研究,提出k3应按公式(3)进行计算:
(3)
式中K为单个剪切连接件的刚度;n为剪切连接件的个数;e为连接件沿梁长的间距;1/π2为折减系数。
有效刚度法计算简便、力学概念清晰、计算精度高,其与精确解析解的误差不超过1.0%,此外,还能给出组合系数的值,非常直观地评价组合梁组合作用的大小。该方法对剪切连接件的刚度无任何限制,其变化范围可以从趋近0到无穷大。本文对钻杆叠合梁的理论计算将采用此方法。
2.3 钻杆叠合梁挠度理论计算
材料参数:钻杆外径D=140 mm,内径d=100 mm,弹性模量E=2.1×105MPa,3根钻杆弹性模量一样。
(1)无剪切连接
无剪切连接时,钻杆间光滑连接,在荷载作用下可自由滑移,上下梁单独工作,有各自的中性层,此时梁的截面抗弯刚度最小,梁之间按刚度之比分配集中荷载。叠合梁截面惯性矩Imin=4.17×10-5m4,跨中集中荷载作用下,根据《装配式公路钢桥》,8 m跨径最大允许挠度ω=L/120=66.7 mm,对应的跨中最大集中荷载54.9 kN。
(2)完全刚性连接
完全刚性剪切连接时,叠合梁是一个整体,此时截面抗弯刚度最大,截面惯性矩为Imax=11.47×10-5m4,8 m跨径钻杆叠合梁跨中允许最大挠度为ω=66.4 mm,最大集中荷载为149.9 kN。
(3)弹性剪切连接
叠合梁中部设置抱箍,可增大钻杆之间及抱箍作用处摩擦力,约束钻杆相对滑移,抱箍越多,约束效果越好,因此把抱箍等效为弹性剪切连接件,用有效刚度法对钻杆叠合梁进行变形计算。有抱箍作用时,局部力通过抱箍传递到橡胶垫,约束钻杆的滑移,不考虑钻杆之间的摩擦力作用。取板式橡胶支座[8]抗剪弹模G=1 MPa,与抱箍和钻杆的接触面积相乘,得出抱箍等效剪切刚度K=G×A=8.8×104N。钻杆轴向刚度为EcAc=1.58×109N,EsAs=3.16×109N,和抱箍的等效剪切刚度相差5个数量级,远大于抱箍的等效抗剪刚度,所以钻杆轴向刚度基本不发挥作用,组合系数为0。
通过组合梁挠度计算的有效刚度法得出废旧钻杆叠合梁的最大承载力在54.9 kN(无剪切连接)和149.9 kN(完全刚性剪切连接)之间;抱箍等效剪切刚度较小,不足以使钻杆轴向刚度发挥作用,对约束钻杆之间的相对滑移无明显作用。
3 钻杆叠合梁试验
中部抱箍作用的废旧钻杆叠合梁实际工作状态介于无剪切连接和完全刚性剪切连接之间,理论分析得出抱箍对约束钻杆的相对滑移无明显作用,所以对抱箍约束的“品”字型废旧钻杆叠合梁实际承载力无法用有效刚度法计算。下面通过室内试验,对钻杆叠合梁的实际承载力和抱箍约束效应进行研究。
3.1 荷载加载工况
试验采用液压千斤顶进行加载,采用地锚栓将支座与反力地坪锚在一起,防止支座翘起,如图4所示。根据理论计算确定荷载加载等级:40 kN前每级加载8 kN,40 kN后每级加载5 kN,每级加载后稳压2 min,叠合梁充分变形后采集挠度数据,跨中挠度达到66.67 mm左右时,停止加载。逐级卸载,采集数据,对试验数据进行复核。试验主要测取跨中挠度数据,在叠合梁跨中安装2个量程100 mm的电子数显位移计,取平均值。

图4 加载装置Fig.4 The loading device
3.2 试验构件设计
试验构件共4组,净跨8 m,中部分别设置0,1,3,5个中部抱箍(A-0,A-1,A-3,A-5),沿梁长均匀分布,如图5所示。
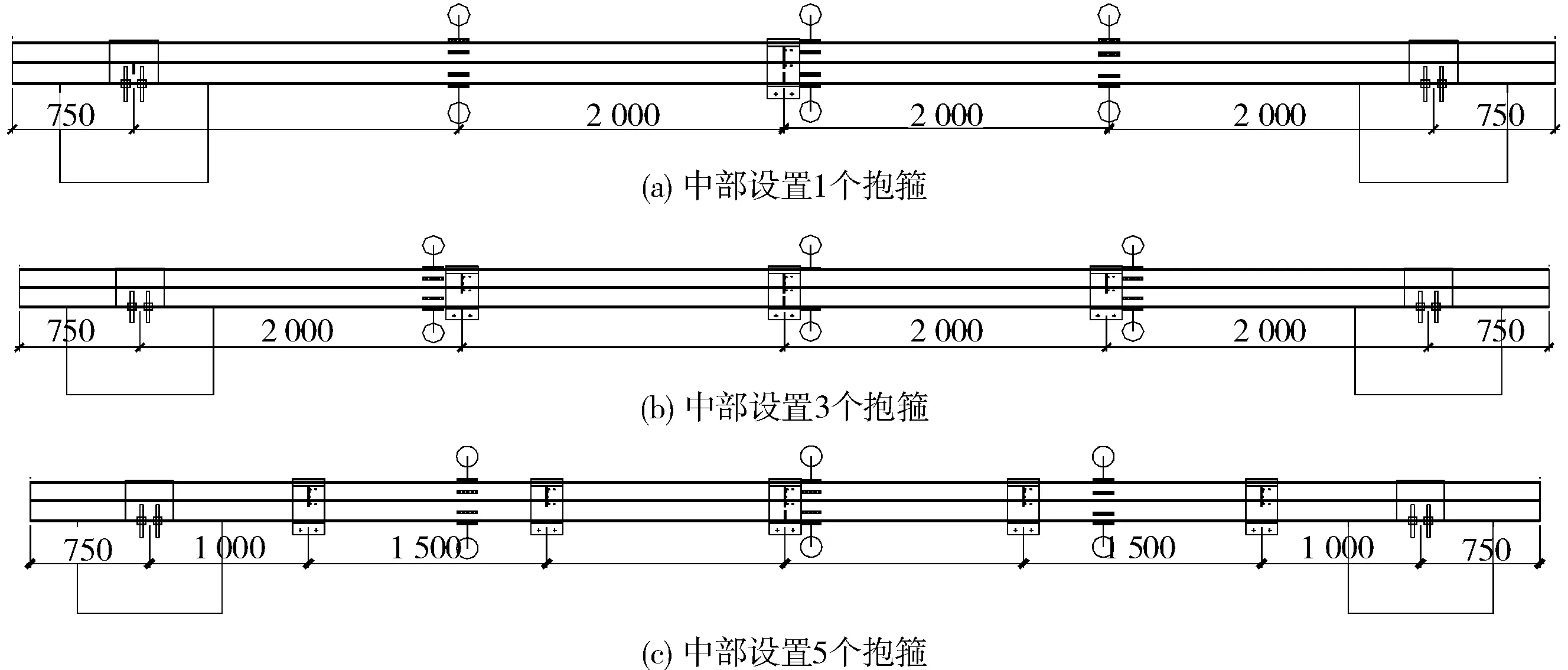
图5 抱箍数量设置Fig.5 Settings for the number of hoops
3.3 试验结果及分析
钻标叠合梁试验数据如表1所示,荷载-挠度曲线如图6所示。

表1 钻杆叠合梁挠度数据Table 1 The deflection data of Composite beam of drill pipes

图6 荷载-挠度曲线Fig.6 Load-deflection curve
(1)由图6看出,当荷载较小时,4条曲线接近,随着外荷载的增大,荷载-挠度曲线开始有较明显区别。可以得到荷载较小时,叠合梁变形小,抱箍无明显作用,随着荷载慢慢变大,变形随之增大,抱箍开始发挥作用,挠度曲线开始有区别,随着抱箍数量增多,叠合梁承载力有不同程度的提高。
(2)A-0构件曲线较其它3条曲线线性关系较差,承载力最低,说明在变形过程中其截面抗弯刚度发生了较大改变。由于A-0构件中部没有抱箍作用,随着荷载的增大,叠合梁变形增大,下部钻杆产生了较大的横向位移,导致截面形状发生改变,抗弯刚度减小,挠度增长变快,最大承载力变小。试验最大荷载45 kN,比理论计算无剪切连接时的55 kN还小。
(3)A-1构件较A-0构件最大荷载提高了10 kN,且线性关系较好。因为在变形最大的跨中位置设置抱箍,限制了下部钻杆的分离,保持截面形状不变,提高承载力,跨中抱箍有关键作用。
(4)A-3构件较A-1构件最大承载力提高了10 kN,且线性关系很好,基本上为直线。随着抱箍的增多可以更好地限制下部钻杆之间的横向位移,保持截面形状不变,提高叠合梁整体性,增大承载力。最大承载力较无抱箍时提高了44.5%,较无剪切连接理论计算值提高了18%。
(5)A-3和A-5构件曲线基本重合,说明多设置的2个抱箍基本上没有作用。抱箍增多可以增大钻杆之间和抱箍作用处的摩擦力,但是和钻杆的轴向刚度相比此力很小,不足以让轴向刚度发挥明显作用,所以抱箍对约束钻杆之间相对滑移无明显作用,和理论分析一致。
4 结论
文章通过对“品”字型废旧钻杆叠合梁理论分析和试验研究,得出以下结论:(1)钻杆叠合梁中部设置抱箍可以明显提高其整体性,增大承载力。(2)8 m跨径废旧钻杆叠合梁,沿梁长均匀设置3个抱箍即可,承载力比无抱箍时提高了44.5%,继续增加抱箍数量对承载力提高不明显。根据理论计算和试验最大承载力,建议“品”字型抱箍约束的钻杆桥使用跨径不超过8 m。(3)抱箍的主要作用是限制下部钻杆的横向位移,保持截面形状不变,提高承载力;跨中变形最大,跨中抱箍有关键作用。抱箍对约束钻杆之间的相对滑移无明显作用。(4)根据跨中挠度理论值与试验值对比可知,有效刚度法适用于不同截面形状、不同跨径的废旧钻杆叠合梁挠度计算。对于跨中抱箍约束的钻杆叠合梁最大承载力取无剪切连接理论计算值的1.2倍;钻杆之间可通局部焊接或刚度较大的弹性剪切连接件连接,提高其承载力,此时用有效刚度法进行承载力和变形计算。

