“接纳”无理数后，如何理解实数？

江苏省海安市城南实验中学八（1616）班 李可欣

老师在介绍 2的历史时，曾提到毕达哥拉斯学派的一个门徒因为发现了 2，却不幸为之付出了生命的代价.老师还说，无理数的出现带来了第一次数学危机.虽然我还不太懂什么是数学危机，但是像圆周率π、2这类无理数确实就在我们身边，也广泛出现在习题之中，我们不得不接纳这类无理数，于是数系再一次扩充到实数系.经过“实数”这一章的学习，我对实数的相关知识或简单的运算也有了一定的了解，借数学周记的机会，进行一次梳理.

1.与实数有关的概念.

2.与实数有关的运算.

在学习这一章时，老师并没有带领我们学习实数的运算，这令我很费解.后来我才发现带有“根号”的综合运算情况很复杂，需要专门学习，在后面（八年级下学期）会有专门的章节学习二次根式的运算.但是我在一些练习册上，也见到一些带根号的算式，比如：

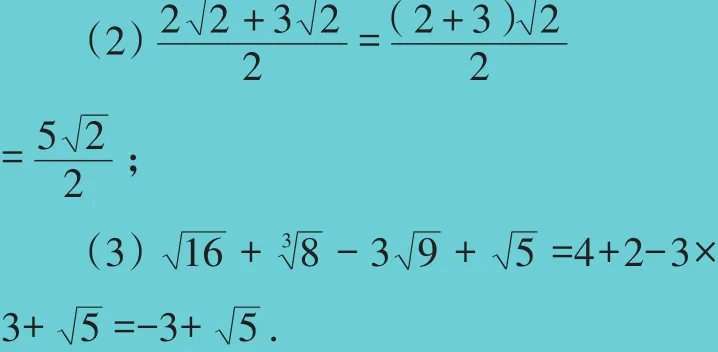
3.点的坐标也可以是无理数.

（1）将点A、B的坐标分别向左平移1个单位后得到的点A′、B′的坐标是多少？

（2）求△A′OB′的面积.

解：（1）点A（2，）、B（5，）向左平移1个单位后的坐标分别为A′（1，）、B（′4，）；

刘老师点评：引入无理数后，数系扩充到实数，需要研究很多内容．实数这一章的重点是开方运算及其概念、实数的概念、近似数等初步知识．确实如小作者所说的，实数的运算是一个大话题，教材上的“回避不谈”是有一定道理的，因为实数的运算涉及二次根式的化简与运算，这会在下学期系统学习，但是从小作者所举题例来看，确实有理数运算中的一些经验（如运算律）、有理数的一些概念（相反数、绝对值）、整式运算的一些经验（如合并同类项）等都在一些简单的实数运算中得到体现和延续．随着学习的深入和认识的丰富，同学们终将会发现：数学在生长，但不是简单地推倒之前的知识或性质，只是在更大范围内接纳、包容．数学在扩张的过程中追求和谐、一致．