数的开方与数系扩充

刘东升

（作者单位：江苏省海安市城南实验中学）

剪拼实验：如图1，将两个边长为1的正方形分别沿对角线剪开，得到四个等腰直角三角形，即可拼成一个大正方形.容易知道，这个大正方形的面积是2，那么大正方形的边长是多少呢？

图1

建立模型：待求的大正方形的面积为2，设它的边长为a，则有a2=2.也就是要把平方运算逆过来思考，即在幂的运算式子“an”中已知指数和幂，逆过来求底数的值.问题简化如下：

若a2=2，求a=_______.

引入新运算、定义新概念：

介绍第六种运算：开方运算.在幂的表达式中，已知指数和幂，求底数的运算，称为开方运算.开方运算的结果称为方根.

从最简单的开二次方说起，即开平方.从定义上看，如果一个数的平方等于a（a≥0），这个数就叫做a的平方根.换句话说，如果x2=a，那么x叫做a的平方根.例如，22=4，（-2）2=4，所以2和-2都是4的平方根.

正数a的正的平方根，叫做a的算术平方根.例如，正数4的正的平方根是2，所以2叫做4的算术平方根.

符号表达：正数a的平方根写成 ± a.例如4的平方根写成± 4=±2.正数a的算术平方根写成 a.例如4的算术平方根写成 4=2.可见，在上面的“问题”中，a= 2.（负值舍去）

性质辨析：一个正数有两个平方根，这两个平方根互为相反数，零的平方根是零，负数没有平方根.算术平方根具有两个非负特性：①被开方数必须是非负数，②算术平方根的值也是非负数.

成果扩大：继续学习开立方运算——立方根.

定义：如果一个数的立方等于a，那么这个数叫做a的立方根.数a的立方根，记作 a3，读作“三次根号a”.

显然，任何数（正数、负数或零）的立方根如果存在的话，必定只有一个.求一个数的立方根的运算，叫做开立方.

数系扩充：有了开方运算，出现了一些开方开不尽的数，我们就有必要将数系进一步扩充到实数了.实数系其实就是对以前学习的所有数的总结，是数系的一次重要扩充，又是今后学习的基础.我们已经知道整数和分数统称为有理数，并规定无限不循环小数是无理数，这样我们把有理数和无理数统称为实数，即实数这个大家庭里有有理数和无理数两大成员.

实数的分类可从两个角度去思考，即（1）按定义来分类；（2）按正、负数来分类.

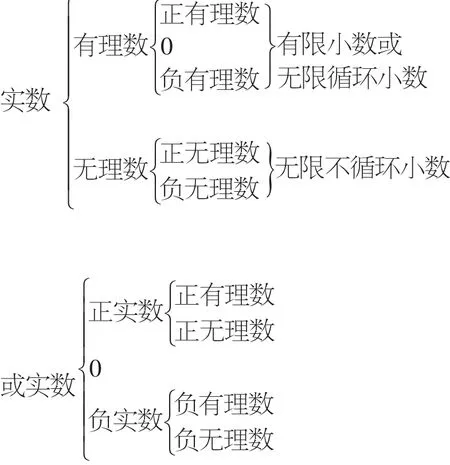
最后，我们列一个“知识结构图”，帮助同学们直观理解“从数的开方到数系扩充”.