基于ANSYS响应面法的发动机曲轴优化设计

吴 辰 ， 侯红玲*， 王 飞

(1.陕西理工大学 机械工程学院， 陕西 汉中 723000；2.陕西汉江机床有限公司， 陕西 汉中 723000)

曲轴是发动机曲柄连杆机构的三大运动件之一，它的作用是把活塞在气缸中所做的往复运动，通过活塞连杆机构转化为自身的旋转运动，确保发动机系统附件的正常运转，其结构对发动机的整体尺寸和质量有很大影响[1-2]。所以，曲轴结构的可靠性对发动机的运转影响巨大。

对于发动机曲轴的研究在汽车工程领域中已成为越来越重要的课题。刘昌领等[3]对六缸压缩机曲轴建立振动学方程，通过ANSYS软件进行八阶模态分析，得出加大曲轴过渡圆角半径等措施可减小曲轴变形和扭振。商海昆等[4]对V6柴油发动机曲轴进行有限元分析，得出了曲轴在各缸最大爆发压力下的薄弱部位，提出了改进措施。刘大龙等[5]对某六缸车用发动机曲轴进行有限元模态分析，得出低频状态下曲轴主要发生弯曲变形，高频状态下发生扭转变形，且频率越高轴颈间连接处的伸缩扭转变形越大。徐中明等[6]利用MSC.Patran/Nastran对单缸发动机曲轴进行有限元分析，改变曲轴材料来使曲轴满足疲劳强度安全系数，并通过发动机可靠性试验验证了仿真的正确性。本文对柴油四冲程发动机曲轴建立三维模型，利用ANSYS软件分析，得出曲轴应力和变形分布图。

1 曲轴结构分析

1.1 结构分析理论基础

[M]{x}+[C]{x}+[K]{x}={F(t)}，

(1)

式中[M]表示质量矩阵,[C]是阻尼矩阵,[K]是刚度系数,{x}是位移矢量,{F}是力矢量。而结构静力学分析中应满足：所受应力必须连续，材料满足线弹性材料和小变形。所有与时间相关选项都被忽略，不考虑随时间变化的载荷和惯性影响。则方程变为：[K]{x}={F}。

本文研究对象是柴油机曲轴，如图1所示。曲轴尺寸：主轴颈半径32 mm，连杆轴颈半径19 mm，连杆轴圆角半径3.5 mm。

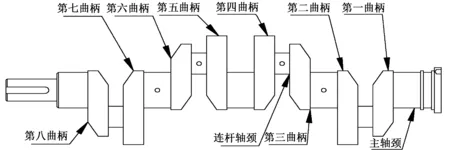
图1 曲轴结构

1.2 参数设置

(1)利用ANSYS软件建立结构力学分析项目，并完成曲轴材料属性设置。材料特性参数见表1。

表1 材料属性

(2)由于曲轴结构较复杂,对曲轴部分参数优化时，初始模型的重建会改变模型相关参数，为了更好地设计过程，将ProE与ANSYS的CAD数据接口互联。在DM模块中采用自动网格划分，共划分23 122个节点，12 696个单元，如图2所示。

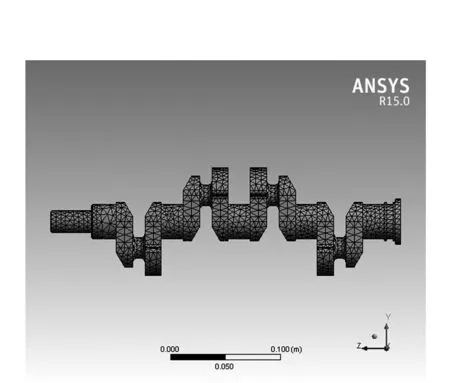
图2 网格划分

1.3 载荷与约束施加

在汽车发动机中，曲轴是连杆机构的重要组成部分，它的作用是将活塞的往复直线运动变为旋转运动，再将这一旋转运动传递给其他机械。曲轴是承受负荷最大的部件，会受到弯曲、扭转、拉压和剪切等力的作用，在常见的故障中，因弯曲疲劳断裂引起的故障率高达80%以上。提高曲轴结构的受力是延长发动机寿命的关键。因此本文通过有限元对曲轴受力情况进行分析，利用响应面法对结构进行优化设计，以提高曲轴的使用寿命。

曲轴的受力如图3所示，假定力边界条件为:载荷沿着曲轴曲柄销轴向呈均匀分布;沿曲轴曲柄销径向，在120°范围内呈余弦规律分布[8-10]。

图3 连杆轴颈载荷分布

在连杆轴颈上120°加载，所有主轴颈120°约束。以第二、三缸爆发为计算工况来说明有限元分析结果。当其点火时，活塞处于止点位置，缸内压力为最大爆发压力，连杆轴颈载荷达到最大值，且受自身重力影响，此时所受径向力为最大，其他位置瞬时受力均小于此位置受力，为计算方便，选取此位置进行受力分析并优化设计。沿曲轴连杆线作用的连杆力为

采用TU-1901双光束紫外可见分光光度计光谱法测定黑米液态发酵酒中总黄酮的含量，以芦丁为对照品，黄酮类化合物中的酚羟基与三氯化铝在中性介质中生成具有特征吸收峰的有色络合物，在一定的浓度范围内，该络合物的吸光度值与总黄酮的浓度成正比[4]。总多糖含量的测定采用苯酚-硫酸法[5]，检测波长490 nm，以葡萄糖来计算，并测定其相对含量。

(2)

其中，fL为连杆力，ph为气缸内活塞上受到的总压力，pz为机构往复惯性力在活塞上的单位应力，φ为连杆摆动角。

进行有限元分析时，以大轴端端面与小轴端端面为约束边界条件，使曲轴不产生轴向位移。

1.4 分析结果

曲轴作为异型长轴类零件，具有轴线不连续、长径比大、结构复杂等特点。从总体上看，曲轴不是完全对称的，因此对曲轴进行有限元分析时以整体为研究对象。对初始尺寸下的曲轴进行有限元分析，施加载荷后等效应变及应力量结果如图4所示。

(a)应变分布 (b)应力分布图4 载荷施加后等效应变及应力量结果

由FEA曲轴受力图可知，在模拟工况下，曲轴连杆轴颈受到径向5000 N的载荷，重力加速度为9.806 6 m/s2，主轴角速度为100 rad/s，力矩为5 N·m。曲轴应力最大处为主轴颈；连杆轴颈与过渡圆角处，最大等效应力为80.313 MPa。曲轴变形主要集中在第三、四曲拐处，最大应变为0.125 9 mm。

曲轴作为发动机关键零件，为保证发动机整体性能及可靠性，应减小曲轴所受最大等效应力和最大应变量。从结论可知，对曲轴进行结构优化时，主要集中在主轴颈、连杆轴颈与过渡圆角处。

2 响应面法优化设计

响应面法是一种采用试验设计理论对指定的设计点集合进行试验,对实体试验或试验数据进行拟合，建立目标和约束的关于设计变量函数的近似表达关系，得到目标函数和约束函数的响应面模型，来预测非试验点响应值的方法[11-13]。

2.1 参数变量设置

优化分析时具体参数及变量优化参数范围如表2所示。

表2 优化参数设置

2.2 优化系统搭建

对曲轴结构参数化设置，优化分析系统搭建(如图5所示)，然后进行响应面灵敏度分析。在workbench中选用Geometry模块，再连接结构分析模块Static Structural，得出Parameters进行数据采集。形成Parameter Set模块与谐响应分析模块Response Surface Optimization连接。最后将优化后的数据输送到初始Geometry模块中。如图5所示，在搭建好的优化系统中得到灵敏度分析。

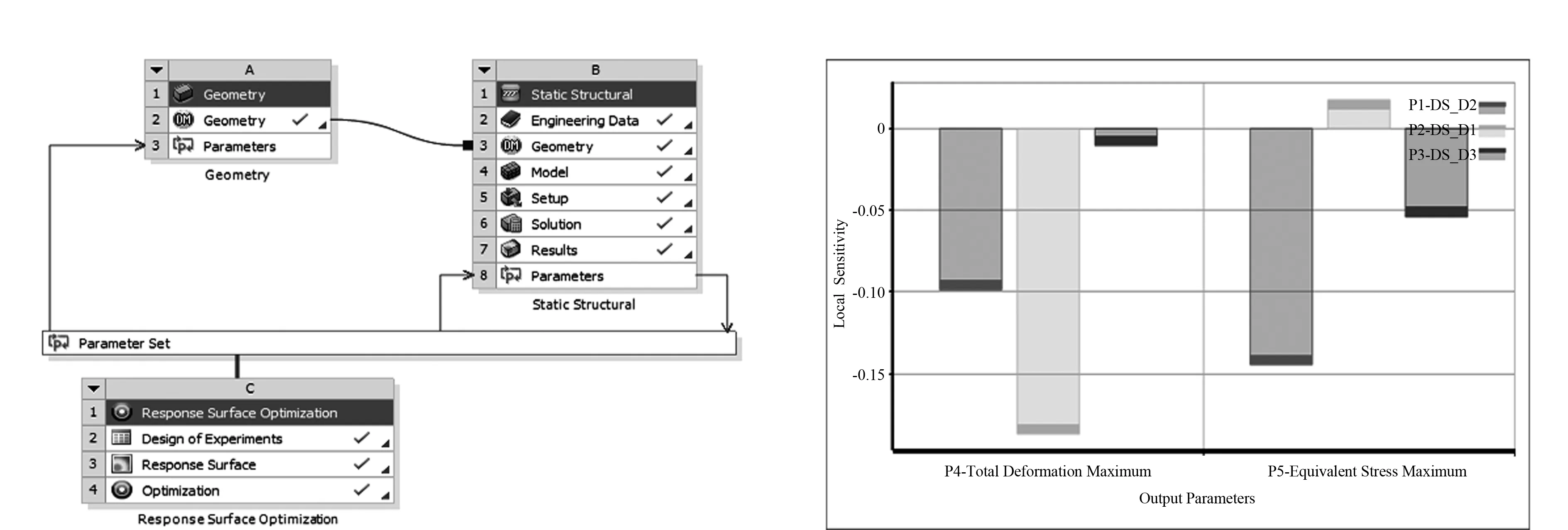
(a)优化分析系统搭建 (b)响应面灵敏度分析图5 优化系统

由图5可确定对应力、变形影响较大的参数：DS-d1与DS-d2，即连杆轴圆角与连杆轴颈半径。

2.3 求解变量

曲轴结构材料为铸铁，优化时铸铁变形不能过大，而对于所需最大应变和最大等效应力应该设置为优化后最大应变的最小值和最大等效应力的最小值小于初始计算值。采用响应面优化是为了得到最优响应点，以提高曲轴的静强度和刚度，因此把曲轴整体最大应变和最大等效应力作为输出参数。输出参数对曲轴结构最大等效变形、应力的响应面图如图6所示。

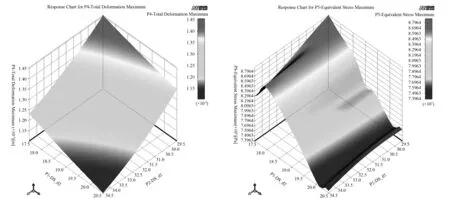
(a)最大等效变形响应图 (b)最大等效应力响应图 图6 响应面云图

然后设置优化目标和约束条件，更新完成后，求解100个候选点，选出输出参数值为最小的3个优化点，如表3所示。从表中分析，选择最佳设计点进行模型重建。

表3 优选设计参数

结构尺寸分析后，选取候选点3进行模型重建，并重新进行静力学分析后可得曲轴最大变形与应力如图7所示。重建后模型分析与候选点3最大变形量最大误差为0.000 02 mm，最大应力最大误差为4.532 MPa。

(a)优化后结构变形分析图 (b)优化后结构应力分析图图7 优化后结果

优化后曲轴结构的最大变形和等效应力，与优化前进行数据对比，结果如表4所示。

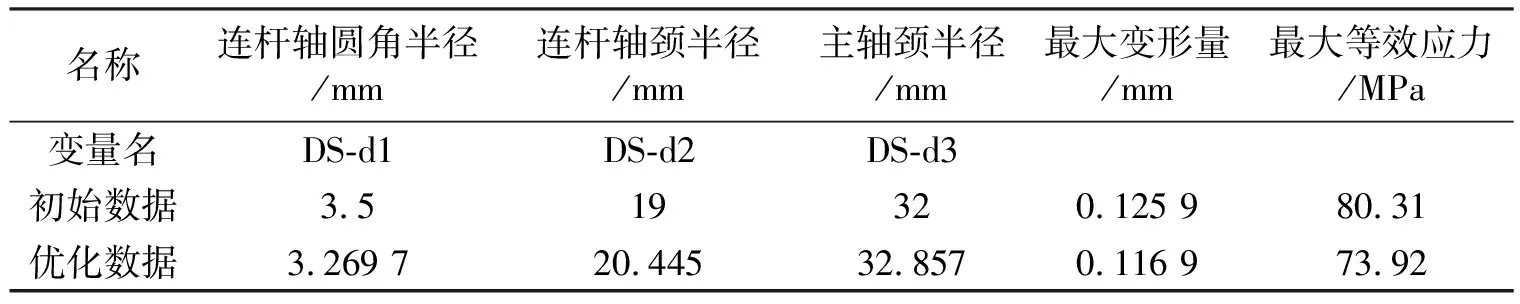
表4 优化前后数据

3 总 结

通过ANSYS软件对四冲程发动机曲轴进行结构优化分析后得知：

(1)在受自重及两端固定情况下施加静力载荷，曲轴的应力集中在连杆轴颈与主轴颈及过渡圆角处，变形量集中在第二、三曲柄及连杆处。通过Equivalent Stress与Total Deformation图可以直观的得到曲轴圆角处的应力与变形情况，为曲轴实际的结构优化提供一定的指导作用。

(2)由表4可知，对曲轴结构参数优化之后，曲轴结构的最大变形量减小了0.009 02 mm。最大应力减少了8.41%。由此可知，优化之后曲轴的静刚度和强度均有一定程度增强，曲轴结构可靠性得到提高。

利用ANSYS软件中的响应面法进行迭代优化，减小设计周期，减少工作量，费用更低，最终得到结构优选点，使得在优选点处，曲轴的应力集中减小，最大变形量减小。这对零部件设计制造提出了新的优化思路，通过搭建响应面系统，对关键参数进行优化运算，拟合优化曲面，直观地反映了各因素之间的交互关系，能够更快速高效的得出优化结果，比以往的设计方法更能找准最优解。

(3)曲轴作为运动件，应考虑曲柄连杆机构作为整体进行研究，对动平衡问题还有待研究。对曲轴网格的划分及载荷的施加分布是否合理，优化设计模型的可靠性，约束和设计变量的选择等，还有待进一步分析。