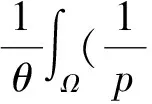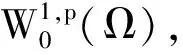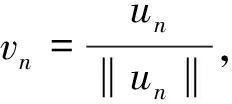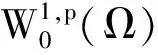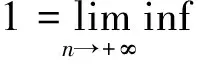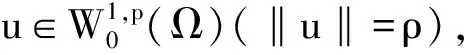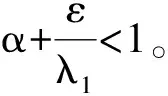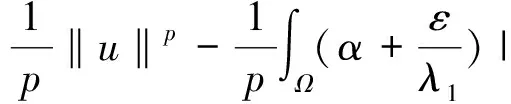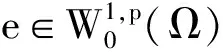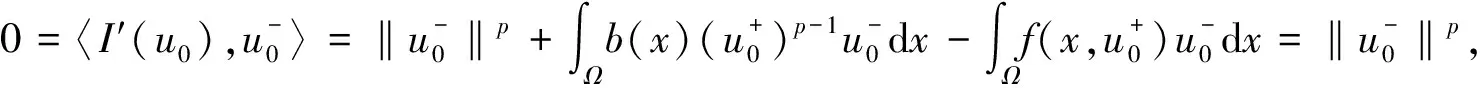超线性椭圆型方程的非平凡解
高婷梅
(陕西理工大学 数学与计算机科学学院, 陕西 汉中 723000)
考虑如下带有Dirichlet边界条件的p-拉普拉斯方程:
(1)
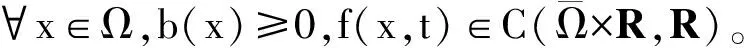
此方程在耗散量子力学等很多物理现象中频繁出现,因此受到人们的广泛关注,如文献[1-6]。文献[1-2]在p=2的情况下,假设函数f(x,t)在无穷远处是超线性时,研究了方程(1)的解。即函数f(x,t)满足以下条件:
本文也将在超线性条件下讨论方程(1)的解。
山路引理是证明方程(1)解的存在性的一个重要方法。为了应用山路引理,要使得方程(1)所对应的泛函的几何结构和临界序列有界,(AR)条件起着至关重要的作用,即

此(AR)条件对于应用山路引理非常方便,但很多函数并不满足(AR)条件。事实上,(f1)就严格弱于(AR)条件。因此,很久以来,人们一直试图削弱(AR)条件,并且得到了许多丰富的结果。例如,可以用以下条件之一代替(AR)条件:
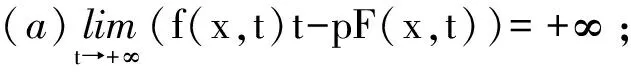
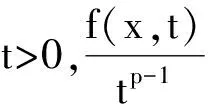
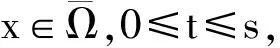
如果条件(b)成立,那么条件(f2)一定成立(证明见文献[4]的注1.5)。并且还可以找到一些函数,例如,f(x,t)=tp-1,当p=2时,f(x,t)t-pF(x,t)=0,显然f(x,t)不满足条件(a)和(b)。但是,由于H(x,t)=f(x,t)t-pF(x,t)=0,则∃θ=1,∀θ0>0,st:

则f(x,t)=tp-1满足条件(f2)。
当p=2时,文献[1]和[2]利用局部环绕定理[5]在超线性条件下讨论了方程(1)非平凡解的存在性,但它们都假设函数f(x,t)满足:

很明显,条件(a)是(c)的一个直接结论,而条件(f2)弱于(a),从而也弱于(c)。本文将在条件(f1)和(f2)下,针对一般的p>1,证明方程(1)非平凡解的存在性。
1 预备知识
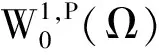
定义设E为实Banach空间,I∈C1(E,R)。如果使得{I(uk)}有界,且
(1+‖uk‖)I′(uk)→0((k→+∞)
的任一序列{uk}(uk∈E)都有一个收敛子列,则称泛函I满足(C)条件。
下面是本文将要用到的一个变形的山路引理,其证明见文献[7]。
山路引理[3]设E为实Banach空间,其对偶空间为E*,I∈C1(E,R),且存在α<β,ρ>0及e∈E(‖e‖>ρ),使得

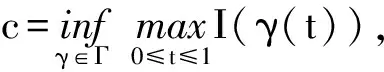
I(un)→c≥β且(1+‖un‖)‖I′(un)‖E*→0(n→+∞)。
2 主要结果及证明
定义如下的C1泛函:
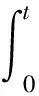
命题1 假设f(x,t)满足条件(f1)、(f2)及以下条件:


则泛函I满足(C)条件。
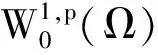
I(un)→c(n→+∞),
(2)
(1+‖un‖)I′(un)→0 (n→+∞),
(3)
(4)
由式(2)、(4),得
(5)
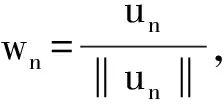
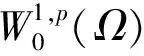
(6)

(7)
由式(3),得
→0(n→+∞),
(8)
(9)
在式(9)中,令n→+∞,得
(10)

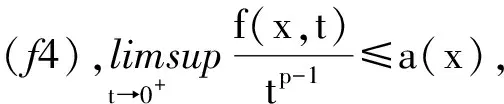
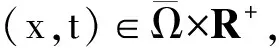

(11)

(12)

(13)
因为I(0)=0且I(un)→c,则由式(13)知,当n充分大时,必有0 (14) 因为0≤tn≤1,则|tnun|≤|un|。从而由(f2)、式(13)、(14),可得 这与式(5)矛盾。所以{un}有界。由Sobolev紧嵌入及标准化方法,知{un}存在一收敛子列。故I满足(C)条件。 命题2 假设条件(f4)成立,则存在常数α∈(0,1),使得 (15) (16) (17) 且有 (18) (19) 由式(19)可知,v是特征值问题-△pu=λ|u|p-2u的第一个特征值所对应的特征函数。由p-拉普拉斯的相关结果可知v≠0,结合式(18)可知,a(x)=λ1在Ω上几乎处处成立,这与条件(f4)矛盾。所以,式(15)成立。 (20) 定理5 假设函数f(x,t)满足条件(f1)—(f4),则方程(1)至少存在一个非平凡解。 证明寻找方程(1)的非平凡解等价于寻找泛函I(u)的非零临界点。由命题1、命题3及命题4,应用变形的山路引理,可以得到泛函I的一个非零临界点u0,且满足I(u0)≥β>0。由条件(f4)、f(x,0)=0,则I(0)=0,所以u0≠0。所以u0是方程(1)的非平凡解。