破冰结构角度对整冰失效模式的影响分析

白旭 周利 陶冶

(江苏科技大学船舶与海洋工程学院, 江苏 镇江 212003)

提要 破冰船破冰过程中整冰的失效模式对于冰载荷的估算十分重要。本文基于力学方法分析了破冰船破冰过程中破冰结构与整冰的相互作用, 得到了影响冰体失效的冰力分量与破冰结构参数的表达关系, 进而确认冰摩擦系数以及坡度角与冰体失效模式的关系。依据北极海冰的摩擦系数范围, 指出当破冰船破冰结构坡度角小于 70°时, 冰体发生弯曲破坏, 当坡度角处于 70°—82°时, 冰体同时发生弯曲和挤压失效, 当坡度角大于82°时, 冰体仅发生挤压失效,同时给出了不同失效模式下冰力的计算方法。

0 引言

近十几年来, 随着全球气候变暖, 北极冰层逐年融化, 各国对连接欧洲、东亚和北美的北极航线的探索不断深入; 与此同时, 对北极地区油气和矿产资源的关注不断升温。极地冰区的通航和科学考察、资源勘探需依靠破冰船开辟航道,破冰航行。因此, 准确模拟破冰船的破冰过程具有重要的理论和现实意义。

当前, 国内外已经开展了大量的关于破冰过程的研究。Riska等[1-2]提出了一些半理论半经验的预报模型, 为早期的破冰船设计提供了有效的方法。将破冰过程划分为四个部分: 冰碎、旋转、滑移以及清除。Wang[3]提出了一种运动的海冰与固定锥形结构相互作用的算法, 并对海冰的破坏过程进行了模拟。Su等[4]对破冰船破冰过程的冰载荷进行了研究, 模拟了整个破冰过程。Nguyen等[5]利用这种冰破碎模式来模拟冰船之间的相互作用。Valanto[6]将冰船相互作用过程分为四个阶段: 破冰、旋转、滑行和清除。他利用三维数值模型来模拟水线面上破冰过程, 碎冰对船舶的阻力根据 Lindqvist的经验公式来计算。Sawamura等[7]也模拟了浮冰在高频力的作用下的动态响应,获得了浮冰的弯曲性能,提出了一套连续接触程序来计算冰力。基于商业软件PhysX, Lubbad和Løset[8]模拟了船与冰相互作用的物理过程。加拿大学者 Sayed和 Barker[9]基于混合拉格朗日方程的质点网格法模拟了冰块与一个锚泊平台之间的相互作用。Zhou等[10-11]利用二维的数值方法来模拟漂浮平整冰与锚泊结构物之间的相互作用。水线面处破冰的过程用几何的方法来模拟,冰的旋转和滑行过程中的冲击力用半经验公式来计算。

国内学者也开展过相关研究。天津大学的Huang等[12]在冰池中对一艘运输船开展了冰阻力模型试验研究, 利用单自由度测力仪测量船模拖航时不同速度下的冰阻力。翟帅帅等[13]模拟了破冰船在直航时的连续破冰模式, 得到了破冰船破冰过程中的冰载荷时历曲线, 并分析了破冰参数对破冰形状以及平均冰阻力的影响。何菲菲[14]利用弹性力学理论对冰载荷进行了求解。王钰涵等[15]针对破冰船在直航情况下的连续破冰模式运用数值方法进行了研究, 得到了破冰过程中的冰载荷时历曲线。桂大伟等[16]对“雪龙”号破冰船的冲撞式破冰模式进行了研究。

以上研究在破冰载荷的计算过程中仅考虑了冰体的弯曲失效, 对于具有大坡度结构的破冰船来说, 其破冰过程中存在的挤压失效方面的研究仍是空白。如果仍采用传统的弯曲失效假设来计算冰层对大坡度结构物的作用, 将出现在垂直于冰层方向的分力过小甚至为负数的情况, 导致冰层局部无法断裂, 局部冰载荷随时间增大而无限变大等不合理现象, 因此需要对现有数值模拟方法开展进一步的完善工作。本文基于模型试验以及实船试验时观测到的破冰船破冰时的物理过程,对船体与冰层相互作用的过程进行分析, 提出了不同的冰失效模式, 并给出了破冰结构物不同倾角下冰载荷的计算模型, 从而可以用来模拟大坡度结构的连续破冰过程。

1 破冰结构与整冰作用的力学分析

冰、水与结构物相互作用的过程是十分复杂的, 在此过程中, 相应的物理现象很难用数值的方法进行再现。因此, 一般需要假定冰的流速相对较低, 进而可以忽略水的抨击作用。

在破冰的过程中, 整冰与船体破冰结构的接触如图1所示。假设其接触表面是平的, 接触面积可由接触长度和接触深度来确定。整冰破碎后产生的浮冰的几何形状是不确定的, 一般可将其假设为扇形, 破冰扇形角度为 θ, 破冰半径根据文献[3]给出的表达式为

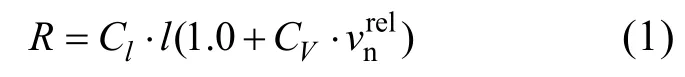
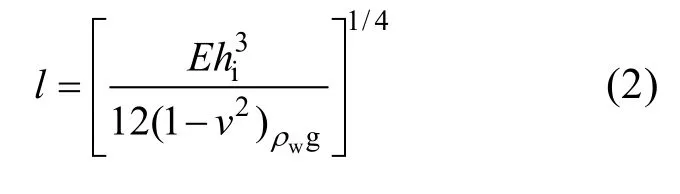
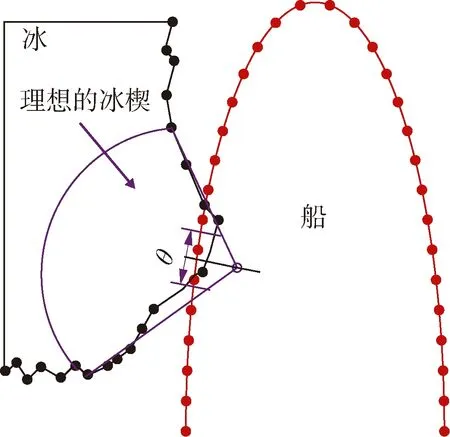
图1 整冰与破冰结构接触示意图Fig.1.Schematic diagram of structure contact with ice

式中，E为弹性模量，hi为冰厚，v为泊松比，ρw为海水密度，g为重力加速度。

破冰过程的冰载荷假设为均匀的, 等效为有效的抗压强度。随着冰与结构接触面积的增加,压碎力逐渐减小。在弯曲破坏前, 挤压的冰力产生于挤压的表面, 并垂直于挤压表面, 对接触表面上产生的局部冰压碎力可以表示为

式中, Ac为接触面积, σc为海冰挤压强度。

船体与冰的相对速度 vrel和力的分量如图2所示,和分别为 vrel沿船体接触点法向和切向方向的分量, 而和分别为垂直面内沿船体接触面和垂直于接触面方向的分量, fh和 fv分别为水平和垂直方向上的摩擦力分量, 垂直于船体表面的挤压冰力 Fcr与摩擦力 fv的合力可以分解为水平分量Fh和垂直分量Fv, 由于冰体在弯曲破坏前没有垂向位移, 所以 fh与相对速度分量成正比, 而 fv与相对速度分量成反比, 根据文献[4]可以表达为

式中, μi为船体与海冰之间的摩擦系数。

2 破冰结构角度与整冰失效

整冰在破冰结构的作用下若发生弯曲失效,如图1所示, 将形成一个开角为θ的冰楔, 在冰楔的顶端受到垂直的载荷, 依据文献[17]对海冰承载能力的估算式为

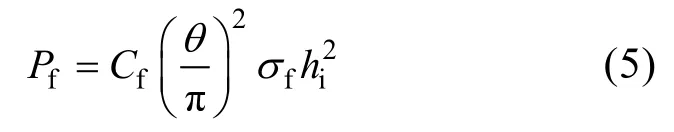
式中, σf为海冰的弯曲强度, hi为海冰厚度, Cf为经验参数。当冰破碎和摩擦力的垂直分量大于Pf时, 冰楔将从弯曲形成的冰边缘裂开并折断, 弯曲失效发生。

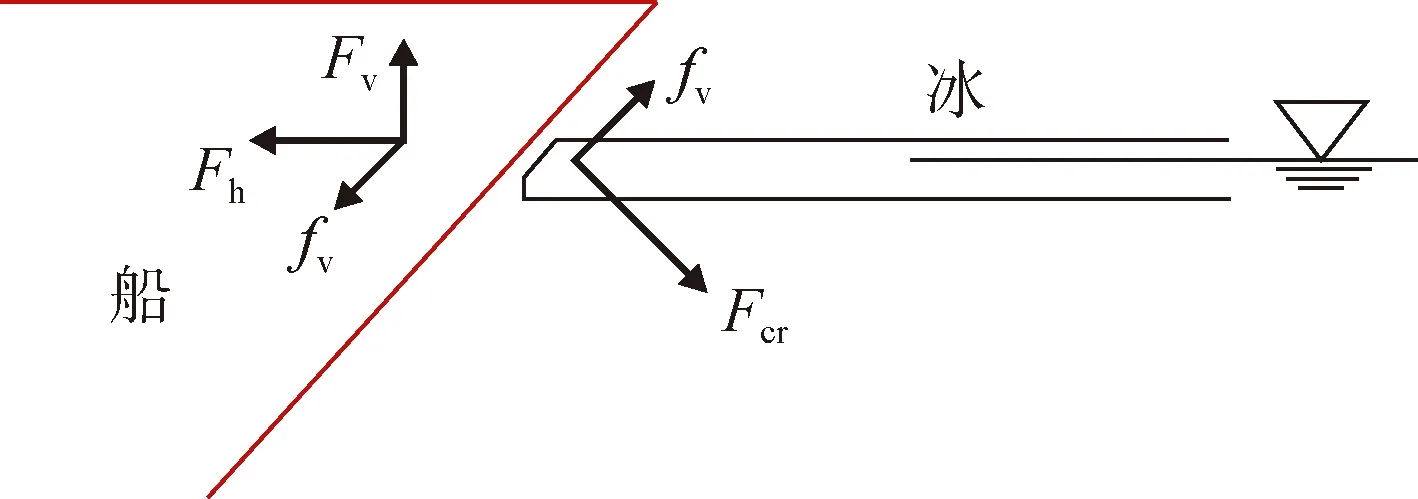
图3 破冰结构与整冰的相互作用Fig.3.Interaction between ice and structure

破冰船的首尾等破冰结构在与冰体相互作用的破冰过程中, 考虑整冰与船体破冰结构的二维相互作用(图3), 根据公式(4)可得:

当船首尾结构的坡度角 α足够大的时候, 作用在冰体上的力垂直分量Fv小至可以忽略。这意味着垂向冰力可能永远不会超过冰的弯曲极限,因此陡峭结构破冰时不会发生冰的弯曲破坏。然而, 这并不现实, 在此前提下计算的冰力也不准确。依据公式(6), 坡度角的极限值依赖于冰与结构相互作用的摩擦系数。

破冰船破冰结构的坡度角对海冰冰体失效模式的影响是十分复杂的, 当 cosα–μisinα=0 时, 摩擦力系数与坡度极限角的关系可以如图4所示,当破冰结构的坡度角大于极限角度时, 冰发生破碎失效; 当破冰结构的坡度角小于极限角度时,冰体发生弯曲失效。根据文献[18], 北极海冰与船体结构的摩擦系数处于 0.05≤μi≤0.15, 由此依据图4的关系, 可得极限角的范围为 82°≤α≤87°。保守起见, 当坡度角大于 82°时, 使用弯曲失效模式将不再合理, 需要对失效模式进行进一步的探讨。

图4 极限角与摩擦系数的关系曲线Fig.4.Relationship curve between limit angle and friction coefficient

关于破冰结构的倾斜角对冰失效模式的影响,文献[19]通过试验的手段进行了大量的研究, 给出了在不同坡度和冰速下冰体失效模式分布图(图5), 本文主要针对冰速较低的情况, 可以看出当倾斜角较小时, 冰的失效模式是弯曲破碎, 随着坡度角的增大, 弯曲破碎的程度越来越小, 而当坡度角达到 70°时, 冰的失效模式主要是挤压破碎。

图5 冰失效模式分布图Fig.5.Distribution map of ice failure mode

因此, 可以说明, 在北极海冰的范围内, 当破冰船破冰结构坡度角小于 70°的时候, 冰体发生弯曲破坏, 当坡度角处于 70°—82°时, 冰体同时发生弯曲和挤压失效, 当坡度角大于 82°时,冰体仅发生挤压失效。

当挤压破碎模式发生时, 根据ISO 19906[20],在不考虑其他限制条件的情况下, 连续作用在结构体上的脆性局部挤压力可以表示为

式中, pG为整体平均冰压力; L为投影到结构物上面的跨度, 其单位是m; h为冰层厚度, 其单位是m;h1为1 m的参考冰厚; m=–0.16为经验系数; n为经验系数, 当冰厚小于1.0 m时, 等于 –0.50+h/5,当冰厚大于等于1.0 m时, 等于 –0.30; CR为冰的强度系数。

当结构物坡度角位于两者之间时, 可以采用插值的方法, 来计算相应的冰载荷。

3 结论

通过破冰船破冰结构与整冰相互作用的力学分析, 得到了影响冰体失效的冰力分量与破冰结构参数的表达关系, 进而确认冰摩擦系数以及坡度角与冰体失效模式的关系, 依据北极海冰的摩擦系数范围, 分析可得: 当破冰船破冰结构坡度角小于 70°的时候, 冰体发生弯曲破坏, 当坡度角处于 70°—82°时, 冰体同时发生弯曲和挤压失效, 当坡度角大于 82°时, 冰体仅发生挤压失效,同时给出了不同失效模式下冰力的计算方法。