大跨度钢桁梁斜拉桥车辆荷载动力效应研究

何博文 周 伟 赖敏芝

(1.中交第二公路勘察设计研究院有限公司 武汉 430056； 2.湖北交投智能检测股份有限公司 武汉 430050)

近些年来，由于钢桁梁的可散拼特性及钢绞线斜拉索运输、施工的便捷性，钢桁梁斜拉桥在山区大跨度桥梁有较多的应用，如新疆果子沟大桥[1]、湖北忠建河大桥[2]、贵州北盘江大桥[3]。大跨度钢桁梁斜拉桥属于高次高静定结构，它在车辆动态激励下的响应十分复杂，车速的不同也给耦合振动增加不确定性，因此，研究大跨度钢桁梁斜拉桥在车辆行驶过程中的振动响应极具现实意义。

国内外有不少学者对斜拉桥的车桥耦合效应进行了分析研究[4-7]，并取得了丰硕成果，但对钢桁梁斜拉桥的动力响应研究较少。本文在已有研究的基础上，根据车-桥耦合基本原理，以鸭池河特大桥为工程背景，取55 t重车作为移动车辆并将其模拟为弹簧-质量块模型，研究大跨度钢桁梁斜拉桥在不同车速下结构的动力响应规律，以期为桥梁的结构健康监测及运营管理中特殊条件下制定限速标准提供依据。

1 背景工程

鸭池河大桥位于贵阳至黔西高速公路，为双塔双索面混合梁斜拉桥，跨径布置为72 m+72 m+76 m+800 m+76 m+72 m+72 m=1 240 m，边中跨比为0.275，桥型立面图见图1。大桥边跨采用预应力混凝土箱梁，梁高8 m；中跨采用钢桁梁结构，横向设置2片主桁架，桁高7 m、宽27 m，节间长度8 m，标准节段长度16 m，桥面由正交异性钢桥面板与7.5 cm浇筑式沥青混凝土组成。主塔采用H形塔，均为矩形空心截面，贵阳侧主塔高243.2 m，黔西侧主塔高258.2 m，斜拉索采用镀锌钢绞线斜拉索，单塔有24对斜拉索，全桥共192根。鸭池河大桥设计荷载为公路-Ⅰ级，设计车速为80 km/h。

图1 鸭池河大桥立面图

2 动力分析模型

2.1 车辆荷载与斜拉桥结构耦合振动模型平衡方程的建立

根据规范[8]，采用公路-Ⅰ级重车(总重550 kN)作为动力分析中的车辆荷载。根据车辆振动分析基本原理，车辆可根据其结构特性简化为不同自由度的弹簧-质量块模型[9-10],简化后的车辆动力模型见图2。

图2 车辆动力模型

图2中v为小车前行速度；mi(i=1,2,3,4,5，下同)为第i个轴的簧下质量，即车轮质量；Mi为第i个轴的簧上质量，即车身质量；ki为车轮刚度，Ki，Ci分别为悬架的刚度和阻尼；yi为车轮竖向位移，δi为主梁动挠度；y6为车身重心位置的竖向位移；θ，I分别为车身的转角和悬架惯性矩；l1，l2，l3，l4，l5分别为各车身质量块距离车身重心的距离；ri为第i个轴所在位置路面不平度。由于研究对象为理想状态下车辆对结构的动力效应，故此处忽略路面不平度效应，即ri=0。

根据车身竖向位移平衡条件、车身转动平衡条件、各车轮平衡条件可得

Ki(y6-liθ-yi)]=0

(1)

Ki(y6-liθ-yi)]=0

(2)

ki(yi+δi)=0,(i=1,2,3,4,5)

(3)

根据式(1)～式(3)，可将车辆的运动方程表示为式(4)矩阵形式

(4)

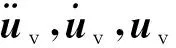
斜拉桥在车辆荷载作用下将会产生变形，且该变形是时变的，将反过来作用于车辆结构，进而影响车辆的运行状态，如此耦合直至车辆通过桥跨结构。桥梁结构受车辆激励的动力平衡方程可表示为式(5)矩阵形式[11]

(5)

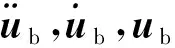
2.2 动力分析工况

模型中车辆由贵阳侧行驶至黔西侧。鸭池河大桥的设计车速为80 km/h，考虑到对于不良天气条件下高速公路的限速原则[13]与个别车辆超速行驶的情况，选取20 ～100 km/h共5个动力分析工况进行研究，分析工况见表1。

表1 分析工况一览表

3 分析结果

3.1 钢桁梁竖向位移

由于边跨混凝土结构整体刚度大，同时跨中位置的竖向位移最大，故取中跨跨中进行研究。提取ANSYS钢桁梁节点位移结果，经整理可得中跨跨中竖向位移、加速度曲线见图3，其中纵坐标为中跨跨中节点位移值、加速度值，横坐标为车辆重心所处位置。

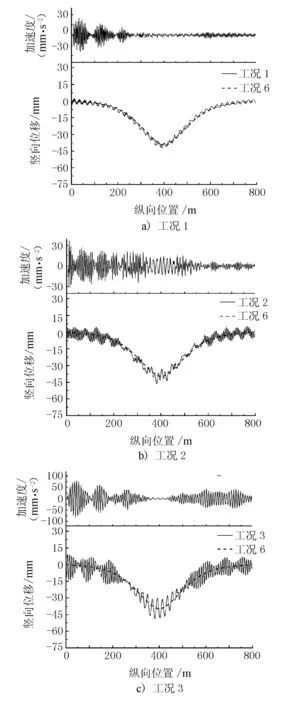
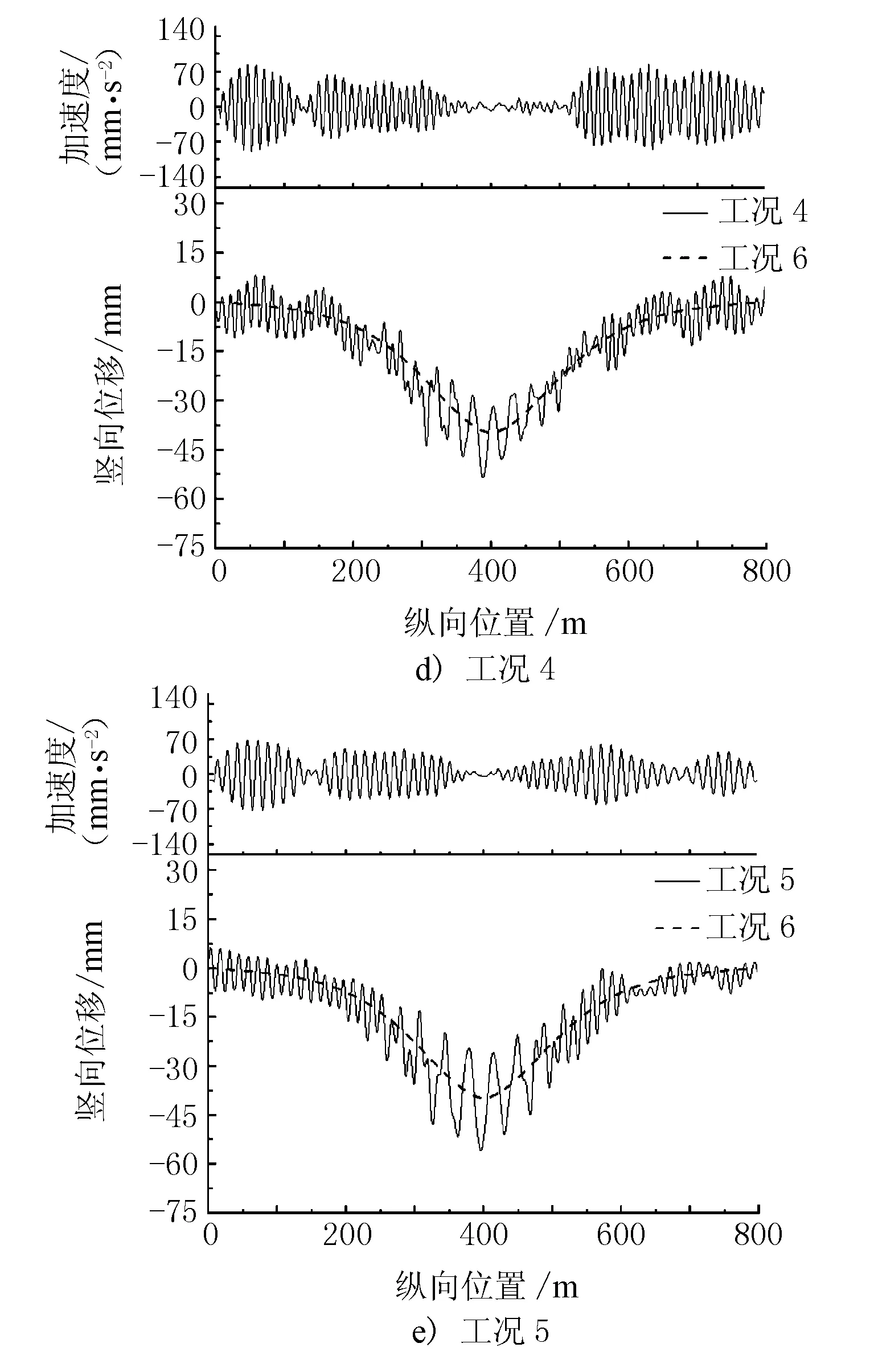
图3 中跨跨中竖向位移、加速度曲线

由图3可见，无论是何种车速，其跨中竖向位移时程曲线均是在静力曲线基础上浮动，且车辆速度越大，跨中的竖向位移振动幅值也就越显著，其中工况1～工况5的跨中竖向位移曲线的最大相邻波峰波谷差值分别为6.1，10.2，15.9，24.3，32.6 mm，而这些最大值均是在车辆行驶至跨中附近时产生的，但此时由于车辆自身质量的影响，使得跨中竖向加速度值较小。同时，车辆行驶在中跨近塔端时，跨中的竖向加速度明显，且随着车速的增加，跨中竖向加速度有增大趋势，工况1～工况5的加速度幅值分别为58.6，70.2，161.5，173.2，141.6 mm/s2。中跨跨中竖向位移极值见表2。

表2 中跨跨中竖向位移极值 mm

由表2可见，低车速时跨中竖向位移最小值与静力解很接近，其最大值亦较小；随着车速的增大，跨中竖向位移的极值均有增大趋势，车辆对结构的冲击效应也越大。

3.2 钢桁梁应力

钢桁梁结构中弦杆是主要受力构件，且车辆作用下跨中位置的弦杆应力较大，故此处选取中跨跨中上、下弦杆进行研究，其中上弦杆轴向应力增量见图4，下弦杆轴向应力增量见图5，图中弦杆轴向应力增量即车辆荷载作用下弦杆轴向应力实际值减去成桥时弦杆的轴向应力，由于低速情况下结构响应较小，限于篇幅，此处仅给出了工况3～工况5的动力响应情况。

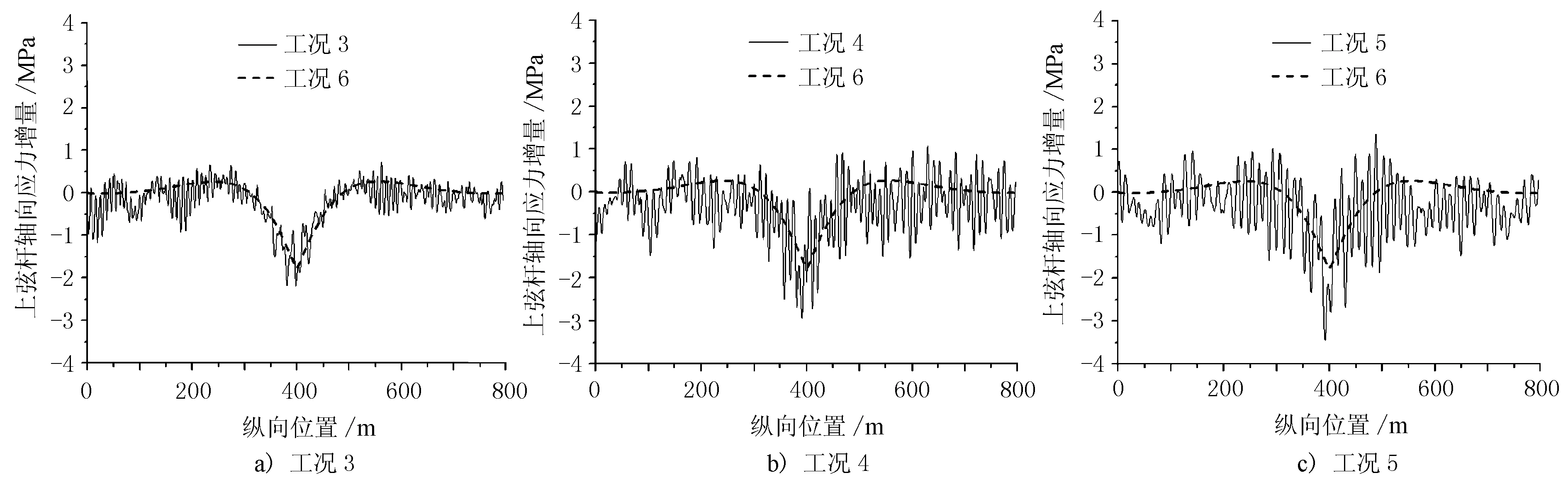
图4 中跨跨中上弦杆轴向应力增量

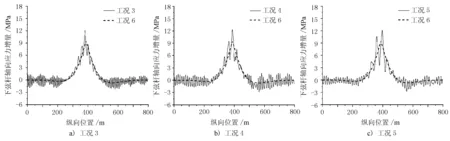
图5 中跨跨中下弦杆轴向应力增量

由图4、图5可见，与跨中竖向位移的结论类似，跨中弦杆轴向应力增量的时程曲线也在静力曲线基础上浮动，且车速的增加会引起弦杆轴向应力响应程度的增大，其中工况5上、下弦杆轴向应力曲线的相邻波峰波谷差值分别达到了3.8，8.6 MPa，高车速将对跨中下弦杆受力状态产生很大的激励作用。跨中弦杆轴向应力增量见表3。

表3 跨中弦杆轴向应力增量极值 MPa

由表3可见，低车速情况下跨中弦杆轴向应力的极值与静力分析差别不大，但在工况3～工况5中，跨中弦杆的轴向应力浮动区间显著增大，车速达到100 km/h时，跨中上、下弦杆的应力幅分别为4.8，15.4 MPa，说明车速越大，弦杆应力响应也越明显。跨中上弦杆在各工况下的轴向应力幅值与静力分析之比分别为1.092，1.413，1.417，1.947，2.335，跨中下弦杆在各工况下的轴向应力幅值与静力分析之比分别为1.05，1.272，1.408，1.494，1.516，说明车速可直接影响弦杆应力的幅值大小。

4 结论

1) 车辆低速行驶时，钢桁梁斜拉桥跨中竖向位移与弦杆应力的极值与静力荷载相差较小，此时车辆对结构的冲击作用较小；随着车速的增大，跨中竖向位移与跨中弦杆应力时程曲线的振幅均显著增大，结构的振动响应更加明显。

2) 跨中竖向位移与弦杆应力的时程曲线均是在静力荷载曲线基础上浮动；当车辆行驶至跨中位置时，跨中的竖向位移与弦杆应力的振幅最大，但由于车身质量的作用，此时跨中位移加速度反而最小。

3) 当55 t重车的车速在100 km/h以内时，跨中的主梁竖向位移与构件应力幅值未产生激增现象，车速共振点不在该范围内。