混凝土梁桥应变监测分级预警阈值设定研究*

胡铁明 汪子龙 韩基刚

(1.沈阳大学建筑工程学院 沈阳 110044； 2.辽宁省交通规划设计院有限责任公司 沈阳 110005)

近年来已建桥梁在运营过程中发生特大安全事故的案例屡见不鲜，已建桥梁安全状态的监控已经成为不可或缺的一项工作。混凝土应变是混凝土梁桥病害分析和状态评估的关键参数，通过对混凝土应变的长期监测，可以了解结构的内力和应力分布情况，通过设定应变预警系统，对桥梁结构进行安全预警[1]。

目前对桥梁监测预警阈值的研究并不多，马中军等[2]引入t分布对弹性模量进行估计，采用修正后有限元模型模拟得到应变的区间预警阈值；李祥辉[3]通过有限元模拟结构受车辆荷载和温度荷载作用，以包络值为阈值设定依据；栾坤鹏[4]采用有限元软件模拟结构受多种荷载组合作用，根据模拟结果确定阈值。可以看出，以上方法都是通过有限元模拟计算来确定预警阈值，但有限元模拟需要基于很多假定条件，计算结果与运营期桥梁真实状态必然存在差异。

笔者通过线性回归分离出应变监测中可变荷载作用效应值，基于日常监测与荷载试验监测数据设定可变荷载作用效应值分级预警阈值，以期对某在役桥梁进行安全性预警。

1 工程概况

以辽宁省某混凝土梁桥(上行方向)为工程依托，该桥全长为990 m，共44孔，跨径布置为10×20 m+8 m+26×20 m+52 m+80 m+52 m+18 m+3×20 m。设计荷载等级：汽车-超20级、挂车-120。2016年12月-2017年4月日均交通量为9 613辆。

以上行方向主桥变截面连续箱梁(跨径组合：52 m+80 m+52 m)为监测对象，采用振弦式传感器进行应变长期监测，监测部位为各孔跨中位置，传感器布置于箱梁内部侧面，距箱梁底20 cm处。

此类振弦式传感器能够同时监测温度与混凝土应变且对结构安全无损，灵敏度及精度较高(±0.1%满量程)，稳定性较好，耐恶劣环境能力强(工作条件：-20～60 ℃)，适合长期观测，由于混凝土与传感器材料热膨胀系数不同，故需要消除温度改变引起的误差。本文采取目前国内最常用的软件温度补偿法消除该误差，计算方法为

Δε=K(f12-f02)+Δt1α-Δt2β

(1)

式中：K为传感器标准系数，由厂家给出；f为频率；Δt1，Δt2分别为传感器和混凝土的温度变化值；α，β分别为振弦和混凝土的线膨胀系数。

2 数据采集结果与分析

2.1 应变-温度相关性

对2017年8月1-7日，桥各孔跨中单个测点的每日整点监测数据为样本空间进行分析，各测点应变和温度随时间的变化趋势见图1。其中应变沿正方向发展表示“混凝土应变增大，混凝土呈现受拉趋势”；反之沿负方向发展为“混凝土应变减小，混凝土呈现受压趋势”。

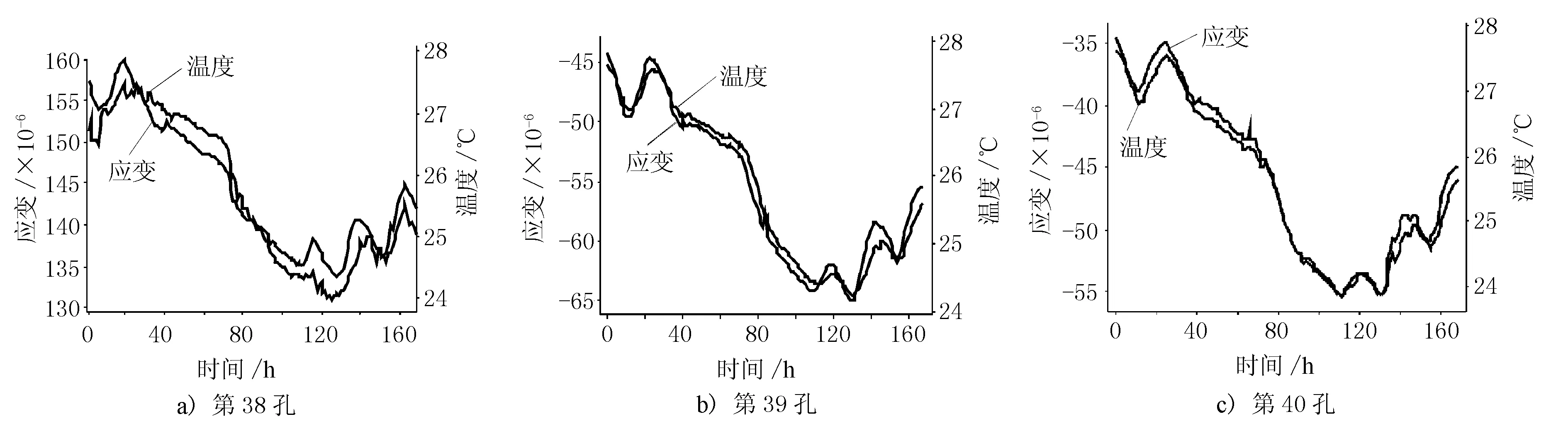
图1 主桥各孔跨中应变、温度曲线图

各测点温度与应变变化趋势均为正相关，各测点应变值不同，第38孔跨中下缘混凝土相对于初始值为受拉状态，其余两孔跨中下缘混凝土均为为受压状态。但变化趋势也基本一致，均为应变减小，混凝土呈受压趋势。

为了明确应变和温度之间的相关性，按温度高低绘制各测点温度-应力散点图，见图2。

图2 主桥各孔跨中应变、温度散点图

由图2可见，应变和温度之间存在明显线性相关性，通过计算其线性相关系数R，进一步验证两者相关性。温度-应变相关系数分别为：R38=0.962，R39=0.986，R40=0.997，说明3个测点应变与温度之间均属线性正相关，温度变化是混凝土应变的主要影响因素。

2.2 应变监测值成分分析

根据桥梁结构分析和混凝土应变理论，混凝土桥梁结构某一时刻的混凝土应变主要由3部分组成，可表示为下式

ε总=εt+εL+εR

(2)

式中：εt为温度应变；εL为荷载应变；εR为收缩徐变应变。

温度应变包括混凝土与传感器两者受温度变化影响产生的应变。本工程应变测量采用具有温度自补偿功能的振弦式传感器，故传感器应变可忽略不计。

荷载应变包括恒荷载应变和可变荷载应变。在结构正常情况下，恒荷载即为桥梁自重，故恒荷载应变为固定值，而可变荷载由于其不确定性，故可变荷载应变为随机值。本文应变监测系统是在桥梁运营5年后建立，应变监测值是相对于安装传感器状态时的相对值，故可以忽略由恒荷载引起的的混凝土应变。

根据混凝土结构收缩徐变理论，混凝土在第1年内完成75%的收缩徐变，随后收缩徐变速度以指数速度下降，并在20年后趋于终值。草河口大桥竣工时间为2011年，距今已7年，混凝土收缩徐变速度已经大幅下降，并且数据采集周期相对于收缩徐变周期过短，由混凝土收缩徐变引起的应变变化可忽略不计。

综上所述，该桥监测系统中应变监测值是混凝土应变温度效应值与可变荷载作用值叠加而成，将温度效应值提出后，即可得到可变荷载作用值。

2.3 温度效应剔除

温度对混凝土应变的影响虽然较复杂，但总体上可以看作是线性关系和非线性关系的叠加，由前文温度-应变的R值可知，两者之间存在很强的正线性相关性，故可以忽略温度对应变的弱非线性作用，因此采用最小二乘法进行线性回归，令

ε=a×t+b

(3)

式中：a，b为待定系数。对于样本值(ti，εi)，使

(4)

的取值最小，即可获得待定系数a，b的估计值。故再令

(5)

(6)

联立式(4)、式(5)可得

(7)

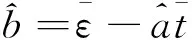
(8)

根据式(7)、式(8)即可求得待定系数a，b的估计值，各测点的应变-温度回归方程见表1。

表1 温度-应变回归方程

综上所述，采用应变监测值作为样本进行线性回归，能够正确地反映温度效应对应变的影响趋势，通过将应变监测值与回归方程计算值相减，剔除温度效应的线性影响，结果见图3。

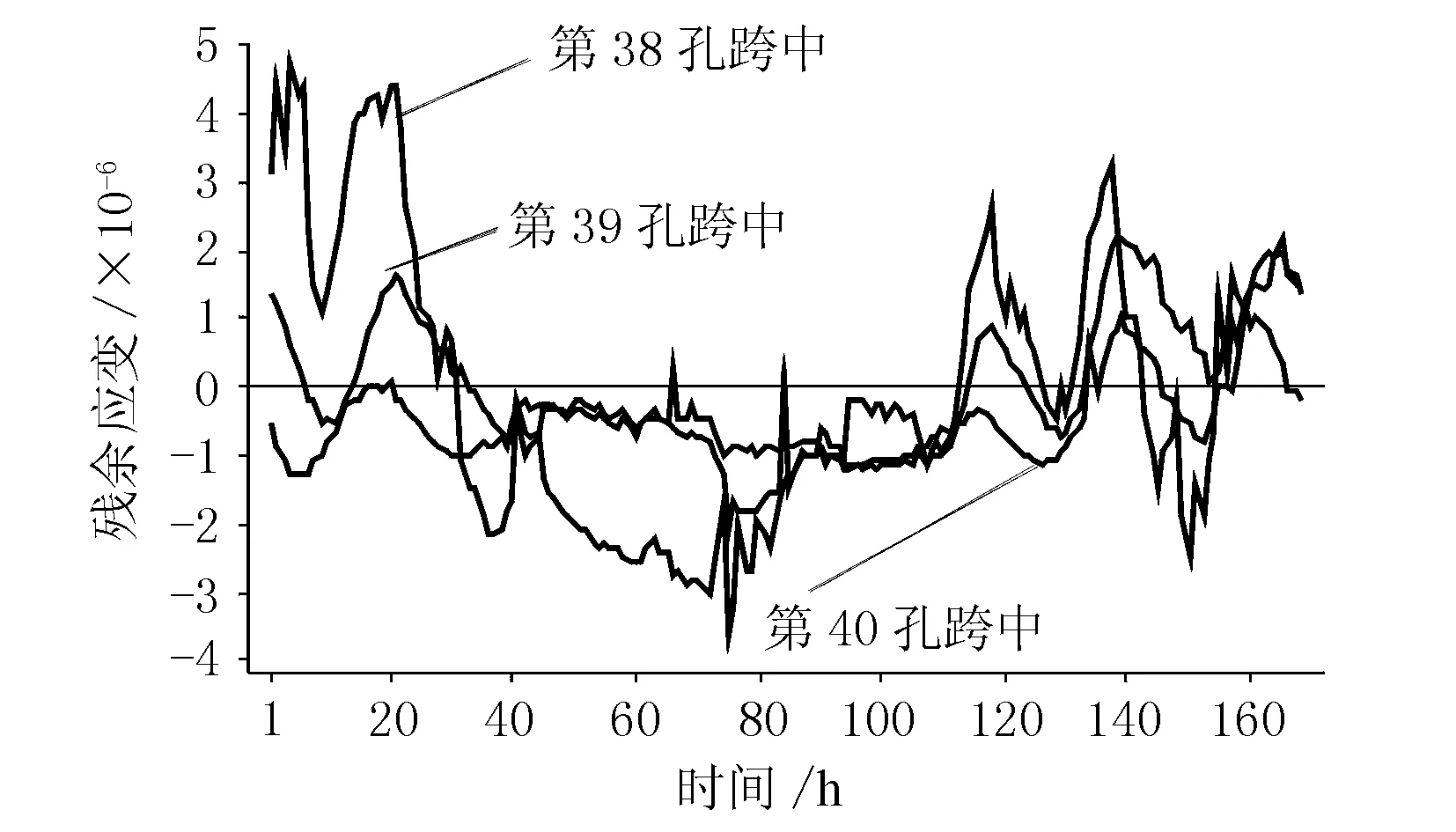
图3 剔除温度效应后的应变残差

由于线性回归方程忽略了温度对应变的非线性作用，故余下的应变残差变化为可变荷载与温度非线性作用的共同影响，但根据前文所得温度与应变的线性相关性系数，认为温度非线性作用影响较小，应变残差主要受可变荷载作用[5]。从图中可以看出，各测点应变残差呈随机分布，均在坐标轴上下(-4×10-6到5×10-6区间内)来回浮动，第38孔明显大于其余两孔，不存在长时间单调性变化。

3 应变残差的预警阈值设定

实现桥梁安全状态实时预警是建立桥梁健康监测系统的重要目标，设定分级预警阈值是预警系统的核心内容。过于保守的预警阈值设定，会导致预警系统过于敏感、谎报、多报，浪费不必要的人力物力；阈值设定过松，则不能及时有效地发挥预警作用[6]。设定低级和高级两级预警阈值，方便监测人员实时观察，应变值一旦达到低级预警级别时，监测人员可立即发现并分析异常原因，及时采取预防措施，防止混凝土应变向高预警级别发展，从而避免安全事故的发生。

由于应变监测系统的实测值为相对于传感器安装时的相对值，无法确定安装前混凝土已产生的应变值，故对监测总应变进行预警难度较大，不易达到理想的预警效果。在混凝土结构弹性工作阶段，可变荷载作用可通过应变值增量反映，不需要确定应变绝对值，且可变荷载作用是运营期桥梁结构安全的主要影响因素，故选择对应变残差进行预警。

结合连续箱梁的的结构特点，分析典型病害为跨中下挠过大和箱梁开裂，本工程应变测点布置在3孔跨中靠近箱梁底部的位置，故选择对混凝土受拉状态进行预警。

3.1 低级预警

低级预警阈值通过计算数据特征参数分析其变化规律，同时确定一个数据变化常态的安全区间，使我们能够以比较高的可靠度相信桥梁状态是安全的，而落在区间外的有理由相信桥梁处于亚健康状态，即设置基于海量监测数据的低级“异常阈值”。

在桥梁结构健康状态下，以一段时间内应变残差的最大统计值为低级预警阈值。当实测应变值与回归方程计算值的残差超出阈值，则触发低级预警。需要注意的是，根据同一测点不同时间段数据获得的回归方程会发生变化，为保证所得的应变残差的准确性，需要通过最新一次采集的温度与应变数据对预警系统中已有的温度-应变回归方程进行更新。

3.2 高级预警

基于荷载试验时应变监测变化量设定高级预警阈值。2017年7月对该桥进行了荷载试验，采用单辆重约350 kN的三轴载重的车列模拟可变荷载进行加载，试验结果表明：各孔正弯矩截面底板应变校验系数与挠度校验系数均在规范常值之内，但各孔截面都存在个别应变校验系数超过规范常值的现象，说明混凝土强度满足设计要求，但材料老化，强度降低；相对应变残差与相对残余变形均在规范限值(20%)之内，说明结构处于弹性状态。

各孔以最不利工况加载时,应变增量监测结果见图4。

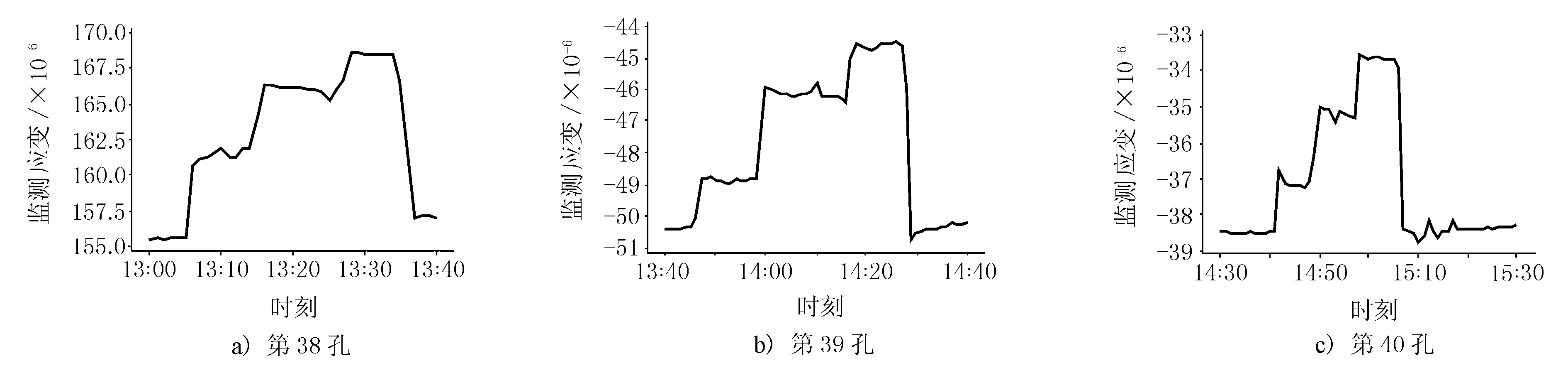
图4 荷载试验应变监测结果

由图4可见，跨中下缘混凝土应变增大，呈受拉趋势，三级加载效果明显，且卸载后应变值迅速恢复至加载前状态。其中第38孔应变变化值明显大于其余两孔，与前文的应变残差分布情况一致，原因可能为梁体刚度降低或预应力损失。由于各工况加载持续时间较短，期间温度变化较小，故可近似认为应变监测值变化完全由加载车辆作用引起。

高级预警阈值的设定：采用荷载试验各孔最大正弯矩工况加载时应变监测变化值作为高级预警阈值。当应变残差超出高级预警阈值时，则认为可变荷载达到设计活载或混凝土结构超出弹性工作阶段，需密切关注桥梁安全状态。

3.3 预警结果

根据上述预警阈值的设定方法，以2017年8月1-7日监测数据与荷载试验时监测数据为基础，设置的两级预警阈值见表2。

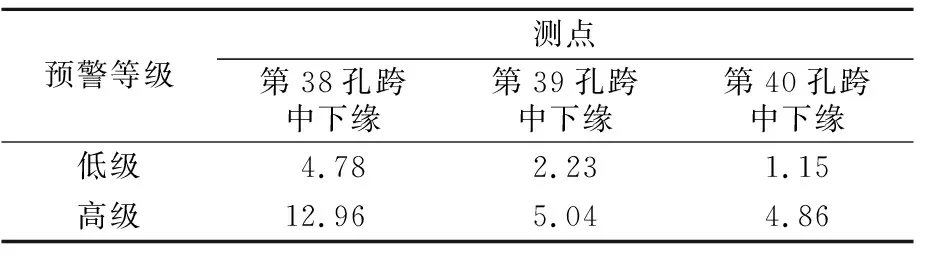
表2 应变残差预警阈值 ×10-6

以主跨第39孔为例，对2017年8月8-9日应变残差进行预警，结果见图5。

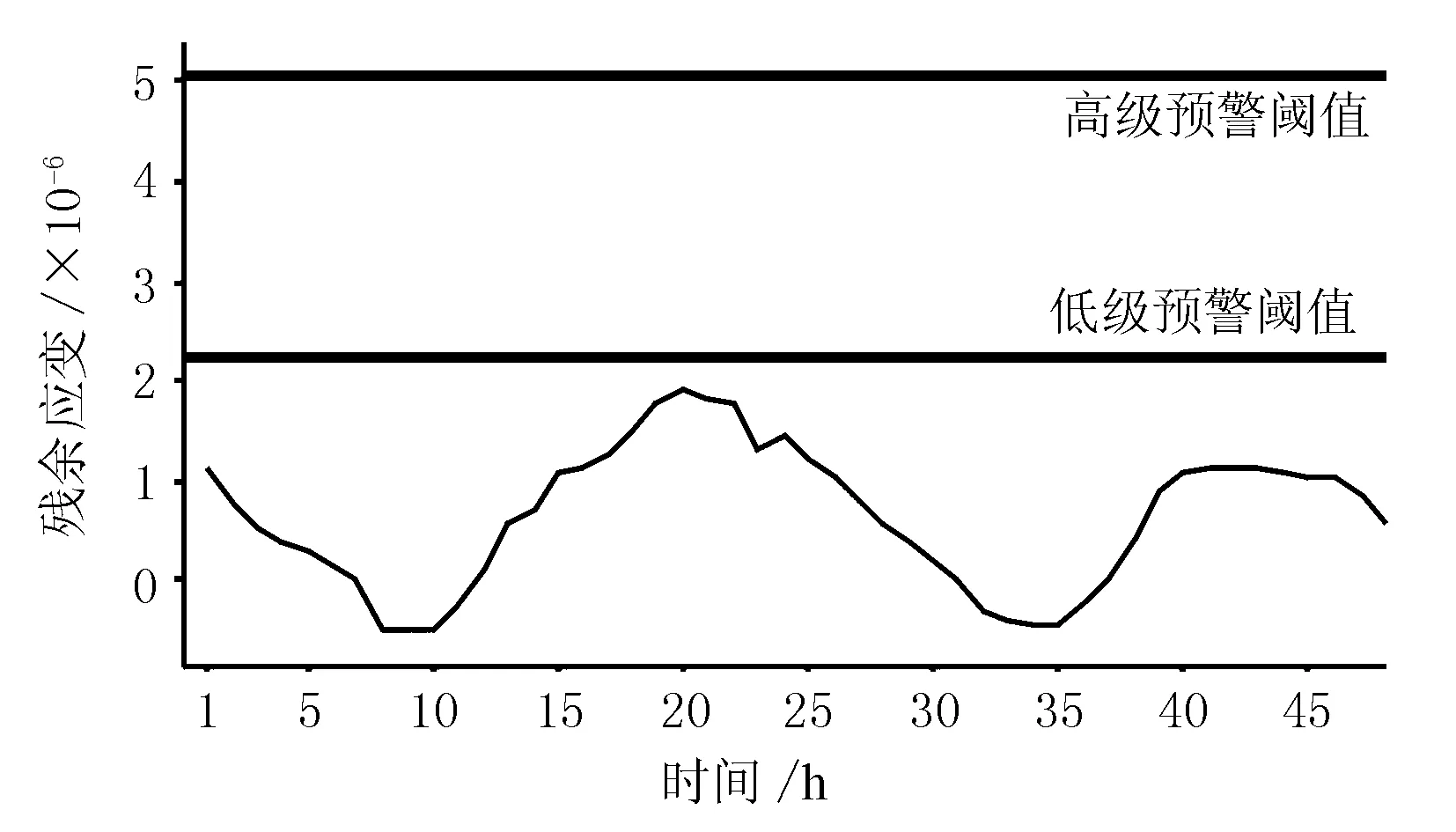
图5 应变残差预警结果

由图5可见，应变残差值与变化趋势符合规律，未超过低级预警阈值。

4 结论

1) 温度是混凝土应变的主要影响因素，两者属于线性强相关，通过线性回归能够提取应变监测中的温度效应值。

2) 结构正常时，可变荷载作用产生的应变残差随机分布在0值附近，无长期单调性变化。采用一定时间内应变残差的最不利统计值和荷载试验最不利工况下监测应变变化值设置的低、高级预警阈值，能够达到预期的预警效果。

3) 在预警过程中，需要通过后续采集的温度与应变数据对温度效应回归方程进行实时更新，保证回归方程及应变残差值的可靠性。