基于双粒子群LDW粒子群改进算法的云计算任务调度算法
吴宇星,刘媛华 (上海理工大学 管理学院,上海 200093)
0 引言
云计算是一种多种技术融合的基于网络的商业服务模式[1]。快速合理的给出计算资源调度方案是云计算中的核心内容之一。当前,云资源调度算法研究已广泛受到相关科研领域学者的关注。采用一种合适的优化算法对其进行高效的调度,缩短任务完成时间并提高资源利用率,一直是云计算科研人员不懈追求的目标。就云计算资源而言,具有异构和动态的特点,进行大规模的资源调度,不仅需要考虑时间因素,还要兼顾负载均衡。由此可知,云计算任务调度问题是一种特别复杂的NP问题,极难求得令人满意的解。
近年来,企业业务需求逐渐向“资源共享与工作协同”的方向跃进,网络技术越来越受到科研人员的关注。其主要研究内容即将把某庞大的计算问题拆分细化为小规模的计算任务,并分配多个计算节点予以处理,再汇总得到最终结果。基于此,国内外不同学者在云计算方面提出了不同方法并应用到了不同领域。在文献[2]中,作者提出了一种同时考虑可靠性、运行时间以及资源调度失败系统方法,同时,使用了一种反射机制分离资源调度过程,并成功应用于云计算资源调度中。文献[3]的作者提出了一种网络服务器的动态模型以及性能控制,同时,设计了增益线性二次型调节器控制器,改进了系统性能的质量,最后,实验证明所提方法的有效性。由于在云计算服务调度环境下,大多数算法收敛速度慢,容易陷入局部最优,为此,文献[4]的作者介绍一种贪婪粒子群优化算法来解决任务调度问题,该算法源于一种虚拟机云平台,相比于传统的粒子群算法,所提出算法能够很快求解出粒子群算法的粒子初始值,使系统性能得到改善。以上方法能够有效解决云计算资源调度问题,然而,很少文献考虑利用改进的惯性权重线性递减的粒子群算法解决云计算资源调度问题。
为将优化计算的相关研究成果更适宜地应用于云计算资源调度,本文提出了一种改进的双粒子群LDW粒子群算法。针对粒子群算法不易全局收敛的问题,本文基于云资源调度问题的数学模型,在惯性权重粒子群算法的基础上,加入随机数扰动,且采用双粒子群的进化机制。并基于2种测试函数和云计算资源调度问题的实际算例,在Matlab GUI平台下采用不同的粒子群算法进行对比试验,以验证算法的有效性。
1 云计算资源调度问题的数学模型
云计算资源调度是一个整数规划问题。通过预先知道某个任务在某个计算节点的执行时间,来实现资源的优化调度。根据不同计算节点的每秒可处理的百万指令数(MIPS),估算其任务执行时间。具体的以花费时间作为优化目标的约束目标模型为:

式中,M={1,2,3,…,m }为任务集合,m为任务数;N={1,2,3,…,n }为节点集合,n为节点数;tij为第i个任务在第j个计算节点上的估算执行时间;Tmax为最大任务执行时间;eij为第j个计算节点上执行第i个任务,若是,则eij=1,反之,eij=0。
具体的最大任务执行时间Tmax的定义如下所述:

具体的目标函数为任务完成时间最短,具体定义如下所述:

式中,cost为最短的任务完成时间。
对于上述云资源调度问题,eij组成的向量是决策变量。当系统具有一定的计算规模时,即是一个特别复杂的NP问题。难于采用诸如线性规划法、单纯形法、牛顿法等常规方法进行求解。粒子群算法由于结构简单,寻优能力强,因而广泛应用于这类复杂的NP问题的求解中[5]。
2 改进的粒子群算法
2.1 粒子群算法
粒子群优化算法是美国心理学家Kennedy和电气工程师Eberhart于1995年首次提出的智能算法[6]。粒子群算法是模拟鸟群捕食的仿真优化算法。设群体规模为N,目标搜索空间的维度为D,第i个粒子的坐标位置向量为速度向量为,粒子群全局极值记为
基本粒子群算法更新迭代计算公式如式(5)所示。

式中:i=1,2,…,N为粒子序号,t为粒子维度,d为迭代次数,c1,c2为加速随机数,一般在0~2之间取值,rand为0~1之间的随机实数。
粒子群算法极易局部收敛。为抑制粒子群算法局部收敛,各种文献对基本粒子群算法进行了不同程度的改进。其中,基于惯性权重系数ω的改进是非常重要的一类改进。具体的包含惯性权重系数ω的粒子群算法更新迭代计算公式如式(6)所示。
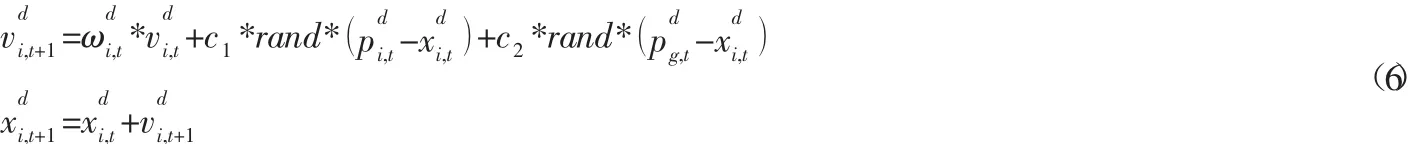
这种改进的算法被广泛应用于各个优化领域。因其与基本算法的计算复杂度类似,但寻优性能却大幅提升。
2.2 惯性权重线性递减策略
惯性权重ω是粒子群算法的重要参数之一。其能够使粒子保持运动惯性,以有能力探索新区域。惯性权重较高,利于全局搜索,能够加快收敛速度,但不易寻到精确解;惯性权重较小,利于局部搜索,容易得到精确度更佳的解,但会降低其收敛速度并增大粒子群算法局部收敛的概率。合适的惯性权重在同时兼顾收敛速度和寻优精度。在粒子群算法的迭代初期,偏重于提升收敛速度;在粒子群算法的迭代末期,偏重于增加寻优[7]。粒子群算法的惯性权重的线性递减(LDW)策略是这样的:整个搜索过程中,惯性权重与进化代数呈现线性递减的关系。其惯性权重ω和粒子群进化代数t的关系曲线如图1所示。
具体的引入惯性权重系数ω的粒子群算法更新迭代计算公式如式(7)所示。
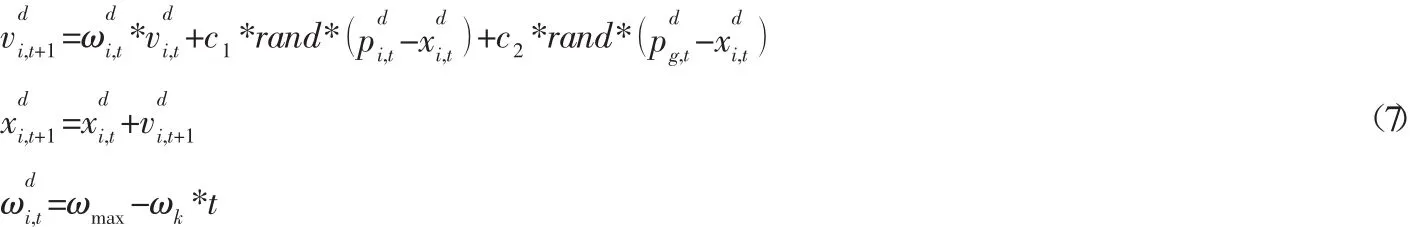
式中:ωmax为初始的最大惯性权重,ωk为惯性权重系数的递减斜率。
2.3 粒子群算法的改进策略
尽管惯性权重线性递减(LDW)的粒子群改进策略能够大幅提升粒子群算法的寻优性能。然而,粒子群算法的实际搜索过程具有非线性和高度复杂的特点,所以惯性权重ω线性递减不能真实反映其实际搜索过程,故而优化效果的改善状况大大受限[8]。因此,粒子群算法迭代过程中,当算法长时间不能得到更佳的最优解时,加入合理范围内的随机数扰动,令惯性权重ω短暂的突然增大,从而抑制粒子群算法局部收敛。具体的增加随机数扰动的惯性权重的线性递减(LDW)粒子群算法的更新迭代计算公式如式(8) 所示。
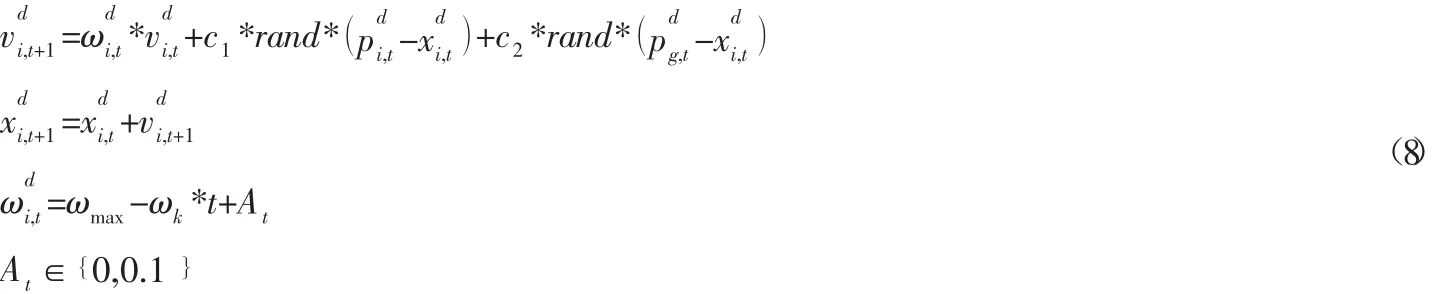
式中:At为惯性权重扰动随机数,在一定的扰动概率下,At∈{0,0.1 },其余,At=0。
具体的惯性权重ω和粒子群进化代数t的关系曲线如图2所示。
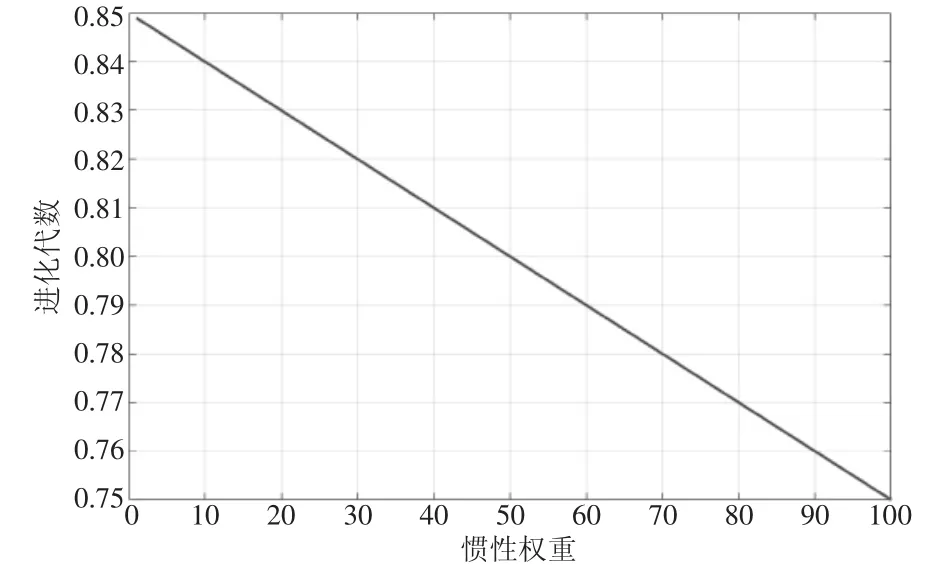
图1 LDW策略下的惯性权重ω和粒子群进化代数t的关系曲线
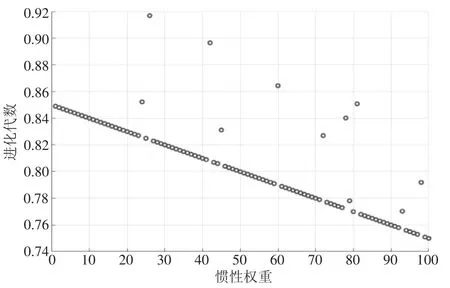
图2 增加随机数扰动的LDW策略下的惯性权重ω和粒子群进化代数t的关系曲线
2.4 双种群粒子群算法
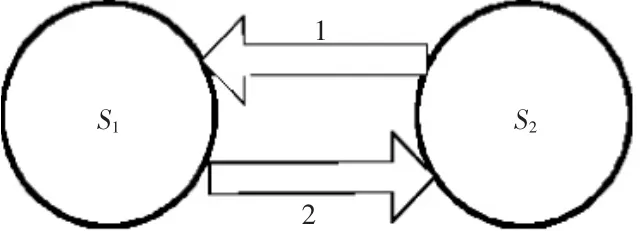
图3 双粒子群最优粒子被交换
尽管粒子群优化算法有着极高的优化搜索能力,但和众多觅食类的生物优化算法相同,粒子群优化算法易于陷入局部收敛。粒子群进化环境和初代粒子群具有一定程度的局限性,当普通粒子群算法进入迭代后期,就会显现出进化缓慢或停滞的不利现象。为此,本文考虑了双粒子群同时进化并进行信息交流的一种改进思路。双粒子群进化机制是一种并行机制,它使用两个粒子群同时进化,并交换粒子群之间优秀个体所携带的进化信息,以打破粒子群内的平衡态以达到更高的平衡态,从而跳出局部最优。粒子群算法在长时间的迭代过程中,最优粒子会对粒子群形成一定程度的“统治”,从而使其极易陷入局部最优。倘若双粒子群同时进化并进行信息交流,那么随着粒子群演化环境的改变,单一粒子群里漫长进化时间里所建立的“统治”权威极易被打破。具体的双粒子群最优粒子被交换的示意图如图3所示:
双粒子群算法的进化流程如下所述:
Step1:随机生成2N个粒子,分别作为初始粒子群1和初始粒子群2。
Step2:分别计算两个粒子群的各个粒子的适应度函数值。
Step3:按照适应度函数值分别对两个粒子群的粒子进行排序。
Step4:查看是否达到最大迭代次数,是则转为Step7,否则转为Step5。
Step5:两个粒子群进行信息交流,也即交换其最优粒子。
Step6:按照粒子群优化算法的更新规则对粒子群的全部个体进行更新,之后转入Step2。Step7:将迭代计算的优化结果输出。
3 仿真实验
3.1 基于测试函数的仿真对比
为考察本文提出的粒子群算法的改进策略是否具有优越性。本文采用2种不同的测试函数对本文提出的改进策略、增加随机数扰动的惯性权重线性递减(LDW)策略和普通的惯性权重线性递减(LDW)策略这3种不同的粒子群算法进行对比测试。以下是具体的测试结果。
(1)De jong函数,又称Rosonbrock马鞍函数,最优解为0.0。具体的De jong函数的公式如下所述。

具体的De jong函数的仿真测试结果如图4所示。
图中,本文提出的改进的LDW策略的粒子群算法最优,求得的近似最优解为: (x1,x2)=(0.9929,0.9994);最优解函数值F(x1,x2)=0.0181。
(2) Schaffer函数,最优解0.0。
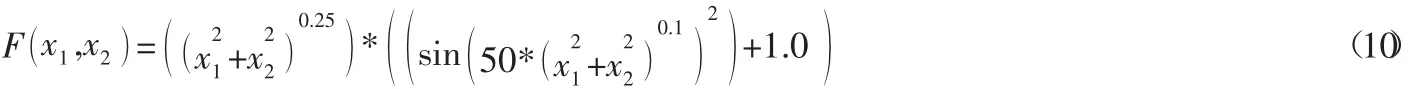
具体的Schaffer函数的仿真测试结果如图5所示。
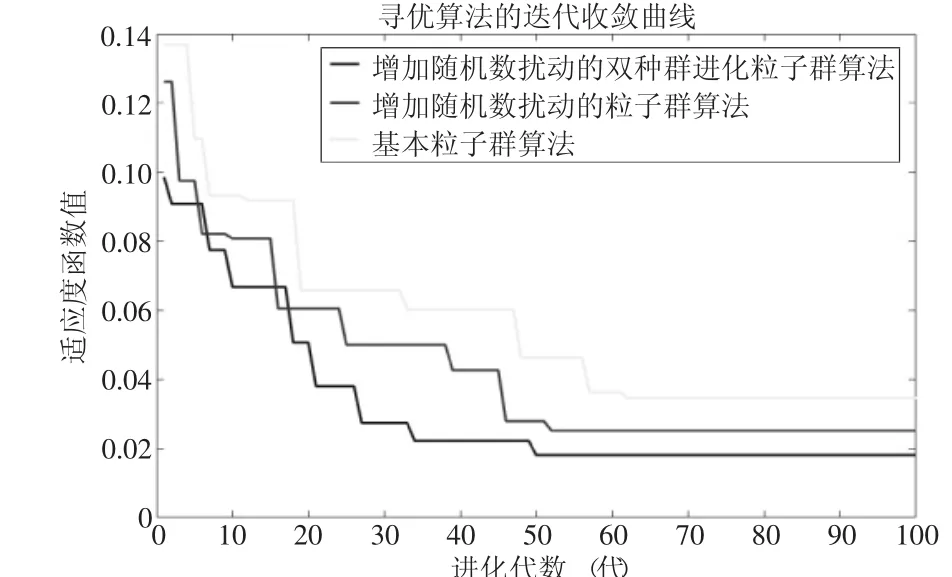
图4 采用De jong函数的仿真测试结果图
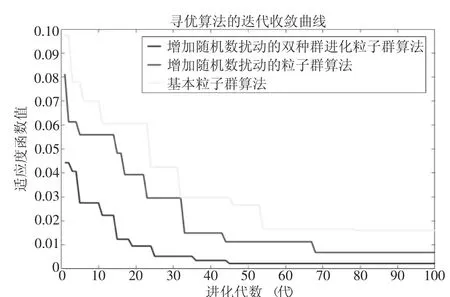
图5 采用Schaffer函数的仿真测试结果图
图中,本文提出的改进的LDW策略的粒子群算法最优,求得的近似最优解为: (x1,x2)=(0.9984,0.9847);最优解函数值F(x1,x2)=0.0022。
3.2 基于实际算例的仿真对比
为验证本文提出的粒子群算法的改进策略相较于其他粒子群算法的改进策略较优。本文采用实际算例对本文提出的改进的惯性权重线性递减(LDW)策略和普通的惯性权重线性递减(LDW)策略的粒子群算法进行测试。本文选用的实际云资源调度问题有4个计算节点和10个任务。以下是具体的测试结果如表1所示。
具体的云资源调度问题的测试结果如图6所示。
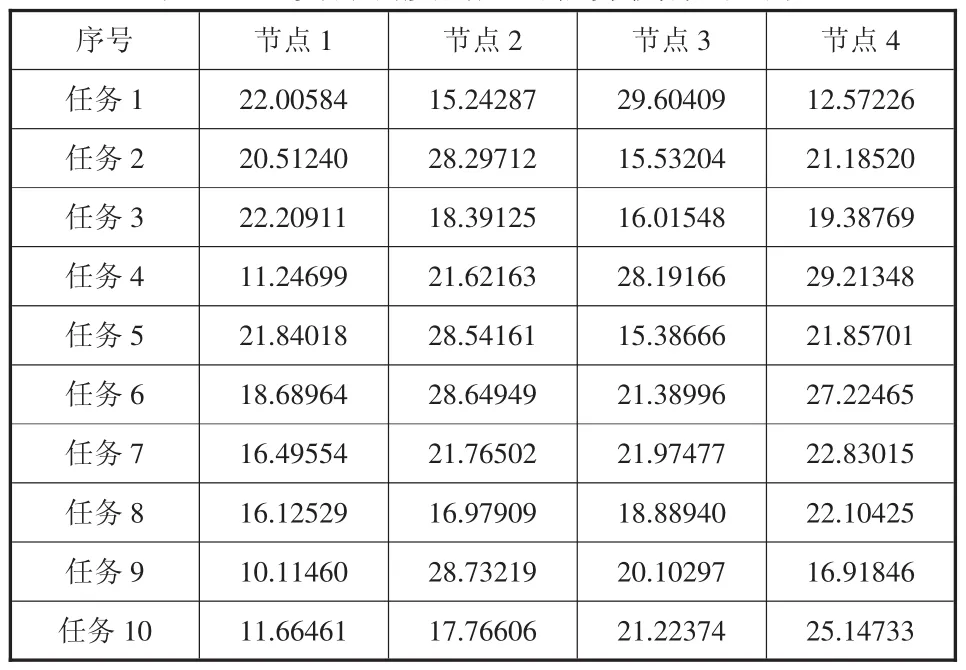
表1 云资源调度问题的估算执行时间表
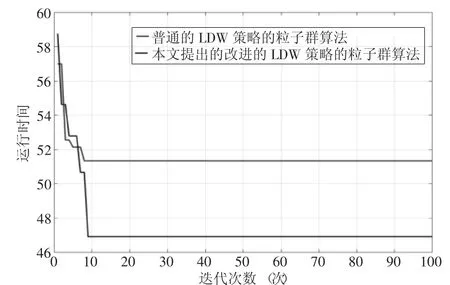
图6 云资源调度问题的仿真测试结果图
图6中,本文提出的改进的LDW策略的粒子群算法较优。普通的LDW策略的粒子群算法求解得到各个任务的执行节点序列为e=[4 3 2 1 4 1 1 3 42],估算任务完成时间为51.488。本文改进的LDW策略的粒子群算法求解得到各个任务的执行节点序列为e=[4 3 3 1 3 2 1 1 42],估算任务完成时间为46.9342。
4 结论
本文基于云资源调度问题的约束目标模型,提出了一种基于双粒子群LDW粒子群改进算法。首先,在惯性权重线性递减的基础上,加入了合理范围内的随机数扰动,以便于粒子群算法更多的进行全局搜索,来抑制粒子群算法局部收敛;其次,为保护粒子群多样性,引入了双粒子群同时进化并随时交流的进化机制,以提升算法的全局优化性能。本文通过2种测试函数和云资源调度问题的实际算例,采用不同的粒子群算法进行寻优。由寻优结果可知,本文改进的算法寻优性能更佳,能够极大程度地提升优化求解的精度。

