立体几何中经典题的突破方法

■河南省商丘市第一高级中学

本文主要介绍解决立体几何中的经典问题的两种方法。

一、几何法

例1 如图1,已知几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD。

(1)求证:BE=DE；

(2)若 ∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC。

考查意图：空间位置关系的证明。

(一)第(1)问的思路分析

1.审条件,挖掘解题信息。

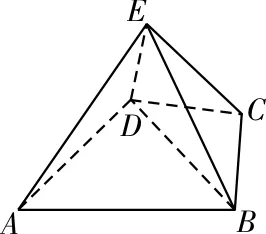
图1

(二)第(2)问的思路分析

1.审条件,挖掘解题信息。

2.审结论,明确解题方向。

3.建联系,找解题突破口。

(三)规范解答

(1)如图2,取BD的中点O,连接CO,EO。由于CB=CD,所以CO⊥BD。

又EC⊥BD,EC∩CO=C,CO,EC⊂平面EOC,所以BD⊥平面EOC,因此BD⊥EO。

又O为BD的中点,所以BE=DE。

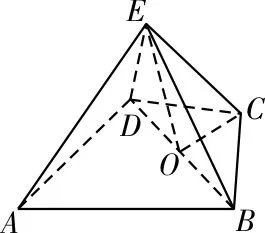
图2

(2)法一:如图3,取AB的中点N,连接DM,DN,MN。

因为M是AE的中点,所以MN∥BE。

又MN⊄平面BEC,BE⊂平面BEC,所以MN∥平面BEC。

又因为△ABD 为正三角形,所以∠BDN=30°。

又 CB=CD,∠BCD=120°,因 此∠CBD=30°,所以DN∥BC。

又DN⊄平面BEC,BC⊂平面BEC,所以DN∥平面BEC。

又MN∩DN=N,所以平面DMN∥平面BEC。

又DM⊂平面DMN,所以DM∥平面BEC。

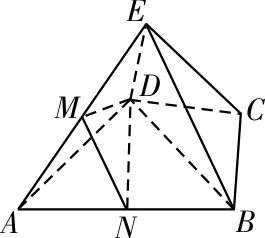
图3

图4

法二:如图4,延长AD,BC交于点F,连接EF。

因为CB=CD,∠BCD=120°,所以∠CBD=30°。

因为△ABD为正三角形,所 以 ∠BAD=60°,∠ABC=90°。

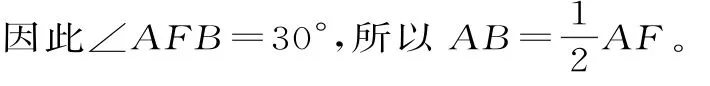
又AB=AD,所以D为AF的中点。

连接DM,由M是AE的中点,得DM∥EF。

又DM⊄平面BEC,EF⊂平面BEC,所以DM∥平面BEC。

(四)名师点睛

证明空间线面位置关系的一般步骤:

第一步,审清题意:分析条件,挖掘题目中的平行与垂直关系；

第二步,明确方向:确定问题方向,选择证明平行或垂直的方法,必要时添加辅助线；

第三步,给出证明:利用平行垂直关系的判定或性质给出问题的证明；

第四步,反思回顾:查看关键点、易漏点、检查使用定理时定理成立的条件是否遗漏,符号表达是否准确。

二、向量法

例2 已知平面图形ABB1A1C1C如图5所示,其中BB1C1C是矩形,BC=2,BB1=4,AB=AC=2,A1B1=A1C1=5,现将该平面图形分别沿BC和B1C1折 叠,使 △ABC 与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A1A,A1B,A1C,得到如图6所示的空间图形。对此空间图形解答下列问题。

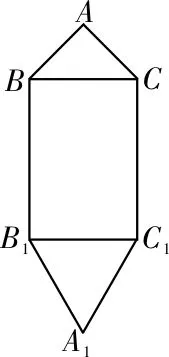
图5

(1)证明:AA1⊥BC；

(2)求AA1的长；

(3)求二面角A-BC-A1的余弦值。

考查意图：空间向量在立体几何中的应用。

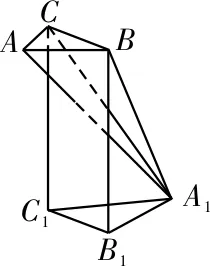
图6

(一)思路分析

1.审条件,挖掘解题信息。

观察条件:四边形BB1C1C是矩形,面ABC⊥面BB1C1C,面A1B1C1⊥面BB1C1C两垂直。

2.审结论,明确解题方向。

观察结论:(1)证明:AA1⊥BC；(2)求AA1的长；(3)求二面角A-BC-A1的余弦值

3.建联系,找解题突破口。

(二)规范解答

(1)取BC,B1C1的中点分别为D和D1,连接A1D1,DD1,AD。

因为BB1C1C为矩形,所以DD1⊥B1C1。

因为平面BB1C1C⊥平面A1B1C1,所以DD1⊥平面A1B1C1。

又A1B1=A1C1,所以A1D1⊥B1C1。

故以D1为坐标原点,可建立如图7所示的空间直角坐标系D1-xyz。

由题设,可得A1D1=2,AD=1。

由以上可知AD⊥平面BB1C1C,A1D1⊥平面BB1C1C,于是AD∥A1D1。

所以A(0,-1,4),B(1,0,4),A1(0,2,0),C(-1,0,4),D(0,0,4)。

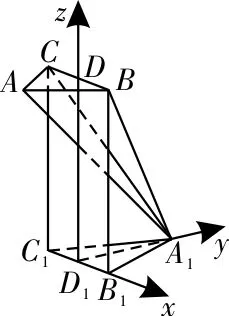
图7

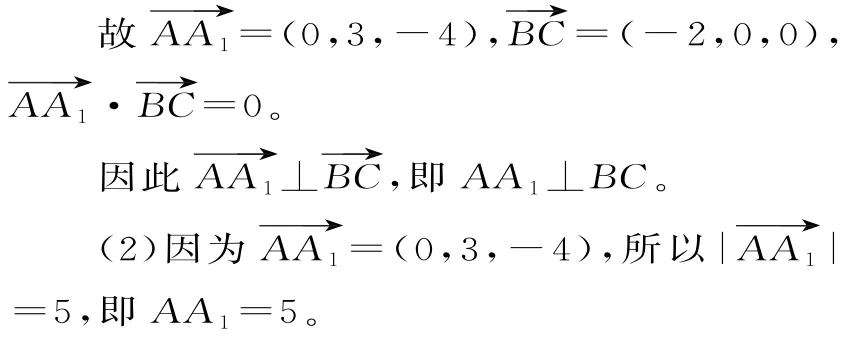
(3)设平面A1BC的法向量为n1=

令z1=1,则n1=(0,2,1)。又因为平面ABC⊥z轴,所以取平面ABC的法向量为

所以二面角A-BC-A1的余弦值为

(三)名师点睛

利用空间向量解决立体几何问题的一般步骤:

第一步,理解题意:利用条件分析问题,建立恰当的空间直角坐标系；

第二步,确定相关点的坐标:结合建系过程与图形,准确地写出相关点的坐标；

第三步,确立平面的法向量:利用点的坐标求出相关直线的方向向量和平面的法向量,若已知某直线垂直某平面,可直接取直线的一个方向向量为该平面的法向量；

第四步,转化为向量运算:将空间位置关系转化为向量关系,空间角转化为向量的夹角问题去论证,求解；

第五步,问题还原:结合条件与图形,作出结论(注意角的范围)；

第六步,反思回顾:回顾检查建系过程、坐标是否有错及是否忽视了所求角的范围而写错结论。