单相PWM整流器相幅控制方法研究

郑 伟，郝保明

宿州学院机械与电子工程学院，宿州,234000

采用PWM方式控制的电压型整流电路(VSR)，在进行升压整流的同时，还可以实现网侧电流的正弦化，并能够完成电能的双向传输。按照网侧进线的相数不同，VSR可简单地分为单相电路和三相电路；按照是否具有网侧电流闭环，VSR又可分为直接电流控制型和间接电流控制型，其中间接电流控制也称为相位和幅值控制[1]。本文针对单相PWM整流电路，研究其交流侧参数在相位与幅值控制方式下的数学关系，构建控制模型并进行仿真。

1 主电路结构与控制模式

在图1所示的单相VSR电路中，网侧电感L用于滤除与载波频率有关的高次谐波；交流侧电阻R包括了滤波电感的等效电阻与电桥中半导体开关的损耗电阻。

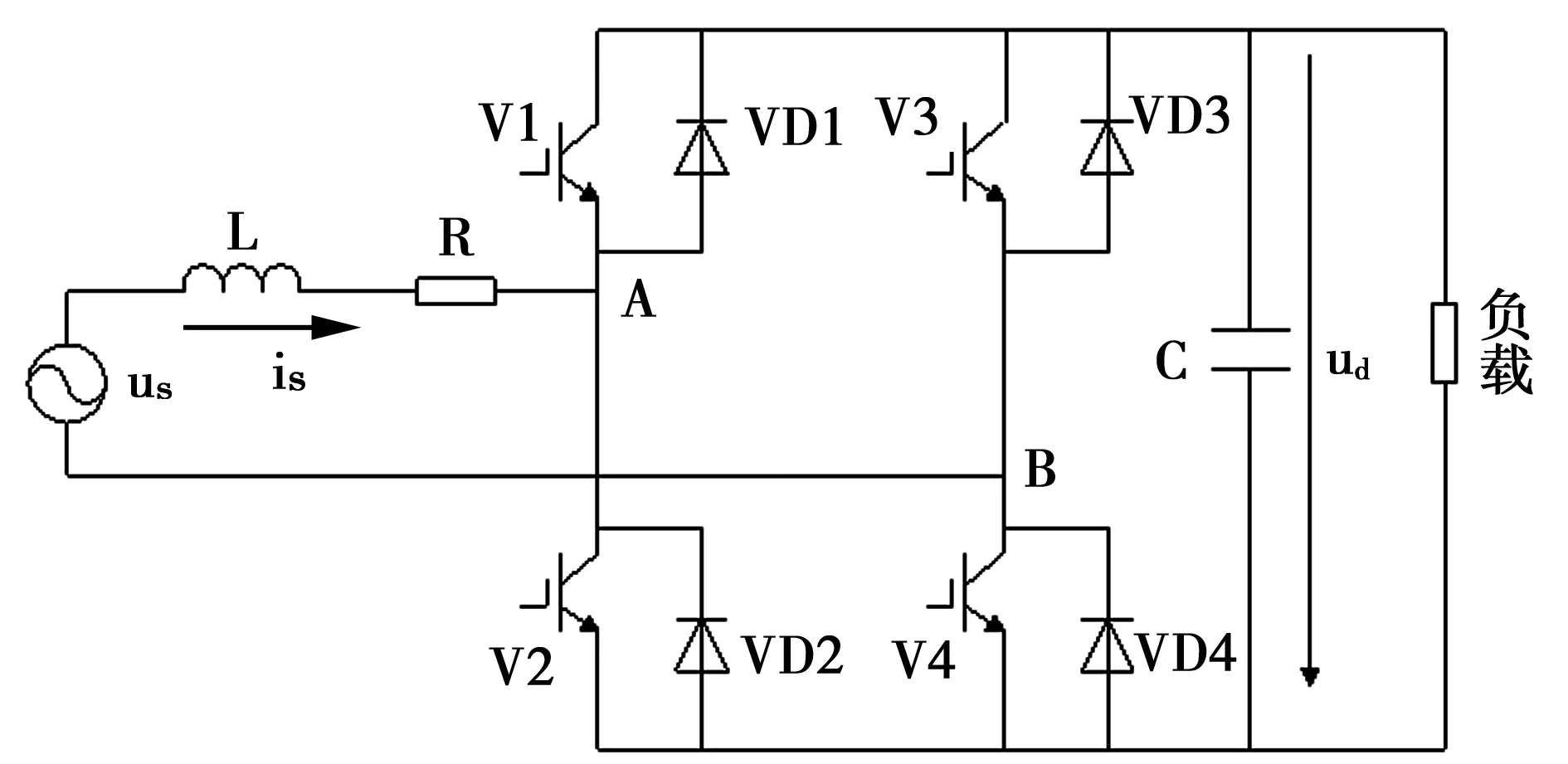
图1 单相VSR主电路

若以正弦波作为调制信号，对电路进行PWM控制，即可在A、B间生成SPWM电压。本文以uAB表示A、B间SPWM电压的基波分量，即uAB是与调制信号同频率、同相位的正弦波。

根据交流侧的回路电压方程，可以得到如图2所示的相量关系图。

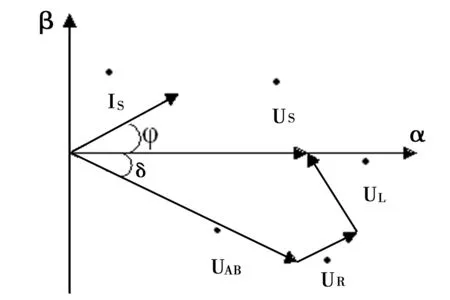
图2 单相VSR交流侧相量关系图

us=uL+uR+uAB

(1)

图中将电网电压us的相量作为参考相量：

us=Us·sinωt

(2)

在静态条件下，uR的相位与is相位相同，uL的相位比is相位超前90°,当交流侧电阻与电感已知时，is与us的相位关系由uAB决定。实际控制中，选取uAB作为直接被控量，通过控制运算生成期望的调制信号，将调制信号ur与载波uc进行比较后，对主电路进行PWM控制，便可在整流桥的输入端得到相位与幅值可控的SPWM电压。因为在控制结构中只利用直流侧电压形成闭环，省去了交流侧电流闭环，通过控制SPWM电压的相位与幅值，从而间接地控制交流侧电流，所以相幅控制方式属于间接电流控制。

2 控制模型的建立

确定调制信号ur与电路中可直接检出参数之间的数学关系；根据ur的数学表达式，设计对应的控制流程。

2.1 数学关系确立

参考三相VSR静态间接电流控制系统的设计方法，寻找调制信号与其他电路参数的一般数学关系[2]；再根据单相VSR的特点，引入新的可检测量，进而推导出满足具体控制需求的调制信号瞬时值表达式。

根据主电路交流侧的相量关系图，将uAB的相量投影到α轴正半轴和β轴负半轴，可得：

uα=UAB·cosδ=Us+UR·cosφ-UL·sinφ

=Us+Is·(R·cosφ-XL·sinφ)

(3)

uβ=UAB·sinδ=UL·cosφ+UR·sinφ

=Is·(XL·cosφ+R·sinφ)

(4)

为表述方便，各瞬时值表达式中的大写字母，如UAB、Us、UR、UL、Is等，分别表示对应交流信号的幅值。

由上述两式，可将uAB表示为：

uAB=UAB·sin(ωt-δ)

=UAB·cosδ·sinωt-UAB·sinδ·cosωt

=uα·sinωt-uβ·cosωt

=Us·sinωt+Is·(R·cosφ-XL·sinφ)·sinωt-Is·(XL·cosφ+R·sinφ)·cosωt

(5)

整流桥输入电压uAB的相位和频率跟随调制信号ur，只要设法找到调制信号ur在电路工作过程中的瞬时值表达式，即可构造控制结构。

设ur=Ur·sin(ωt-δ)

=Ur·cosδ·sinωt-Ur·sinδ·cosωt

(6)

(7)

式中,Uc表示载波信号幅值，ud表示直流侧电压。ud的波形实际是由A、B间SPWM电压波形的上下包络线组合而成，其中不仅有直流分量，还包含交流分量；且其数值受到直流侧电容容量等多方面因素的影响[3]；此处将ud引入uAB的表达式，使其不仅出现在负反馈支路中，还进入控制运算流程，有利于系统的稳定。

在设计三相VSR的控制系统结构时，通常利用b、c两相电网的二次侧电压信号构成关于a相电网电压二次侧信号的余弦表达式，从而构造调制信号ur的完整表达式；在进行单相VSR直接电流控制电路的设计时，为便于坐标变换，可以利用延时电路得到余弦信号[4]。在此，我们引入电网电压与交流侧电感电压的瞬时值表达式，分别构成ur表达式中的正弦与余弦函数项。根据PWM整流器交流侧的相量关系：

is=Is·sin(ωt+φ)

(8)

uL=UL·cos(ωt+φ)

=UL·cosφ·cosωt-UL·sinφ·sinωt

(9)

由(2)(9)，可得：

(10)

结合(5)(6)(9)(10)，可令：

Ur·cosδ·sinωt=K1·Us·sinωt+K2·Is·Us·sinωt

(11)

(12)

其中，K1、K2、K3为待定系数。

再结合(5)(6)(7)(11)(12)，可得：

=Us·sinωt+Is·(R·cosφ-XL·sinφ)·sinωt-Is·(XL·cosφ+R·sinφ)·cosωt

(13)

比较上式中的对应项，可得待定系数分别为：

(14)

2.2 控制结构设计

将(11)(12)代入(6)，可以得到调制信号的表达式：

=K1·us+K2·Is·us-K3·Is·(K4·us+uL)

(15)

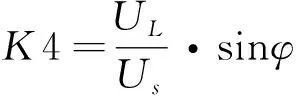
(16)

根据式(15)，设计出单相PWM整流电路在相位与幅值控制方式下的控制系统结构如图3所示。

要在实物电路中实现上图所示的控制方式，除检测直流侧电压外，还需利用两个电压互感器分别检出电网电压与交流侧滤波电感的端电压。再结合电路参数的计算，便可确定K1、K2、K3、K4的具体数值，进而得到单相PWM整流器相幅控制所需要的调制信号。

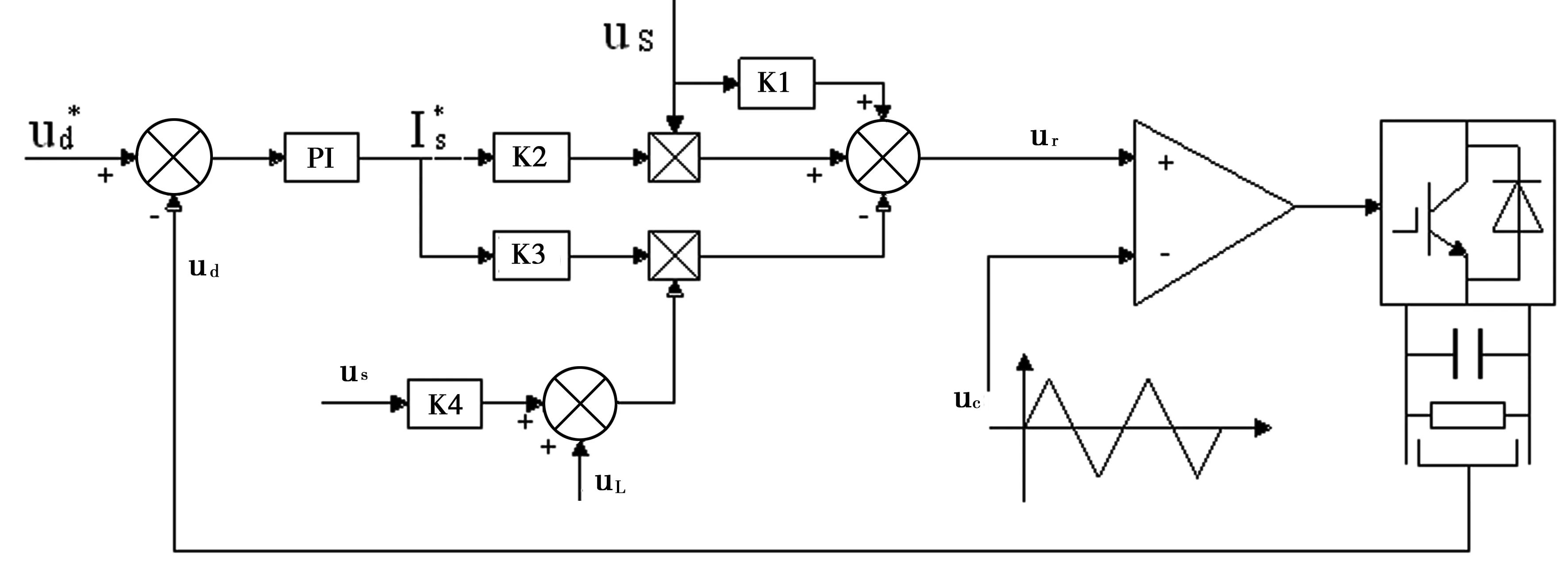
图3 单相VSR相幅控制系统结构图

3 仿 真

在Matlab/Simulink中构建单相PWM整流器相幅控制仿真电路，采用直流侧电压单闭环控制结构，电压控制器采用比例积分调节器。主要参数：交流电网电压有效值220 V/频率50 Hz，交流侧滤波电感0.01 H，交流侧电阻1Ω，直流侧电压给定值620 V，直流侧电容2 000 μf，负载电阻200Ω，电压控制器Kp=3.5、Ki=12，双极性三角波频率为1 kHz。

考虑到电路主要由电网电压与储能元件完成回路电压平衡和功率交换；在进行直接电流控制时，常将交流侧电阻省去[5,6]，从而简化控制系统结构。而相幅控制方式的系统结构与电路参数有关，故在仿真时仍将交流侧电阻保留。

取网侧电流与电网电压的相位差φ=0，载波幅值Uc=1，计算出各控制支路中待定参数的具体数值；为保证各控制支路输出信号幅值不超过载波幅值，进而保证直流电压的稳定性，在调制环节中，将实际的载波幅值设定为15。仿真电路如图4所示。

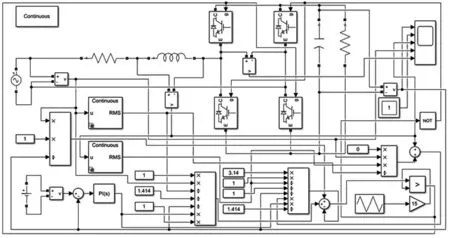
图4 单相VSR相幅控制系统仿真电路

图5为PWM整流器通过相幅控制得到的直流电压与网侧电流波形：直流电压在电路开始工作后3s进入605 V～635 V范围内，并且实现了长时间稳定。网侧电流实现了正弦化。从控制指标上看，系统的阻尼较大，反应时间较长。从相幅控制方式本身的特点上进行分析，由于控制系统结构是根据静态过程建立的，并且只有直流侧电压的单闭环，因此响应速度较慢；另一方面，因为不存在双闭环之间调整作用的相互影响，所以在进入稳态后直流电压的波动较小。当直流侧负载电阻阻值发生变化时，直流电压受到的影响比直接电流控制时更为明显[7]，当负载变化较大时，需同时调整直流侧电容容量及PI调节器参数才能保证直流电压趋向稳定，这也印证了间接电流控制系统的控制效果易受电路参数变化的影响，即鲁棒性较差。

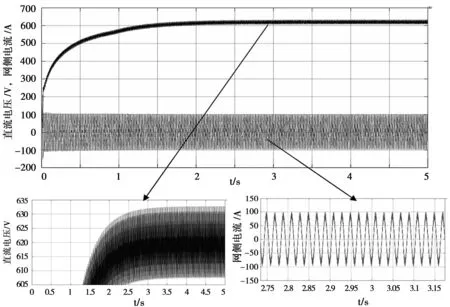
图5 单相VSR直流电压与网侧电流波形

图6为整流器交流侧各电压波形：整流桥按照升压斩波的方式运行，稳态时SPWM电压的幅值达到620 V，比电网电压幅值311 V高出近一倍，滤波电感上需要产生很高的感应电动势以维持网侧电流的连续，仿真电路运行得到的电感电压幅值超过900 V。交流侧等效电阻阻值1 Ω，其电压波形与网侧电流波形一致，该波形并未在相位上与电网电压保持一致，说明相幅控制作为一种间接电流控制方式，其对电流相位的控制效果与直接电流控制方式相比，存在明显的差距。

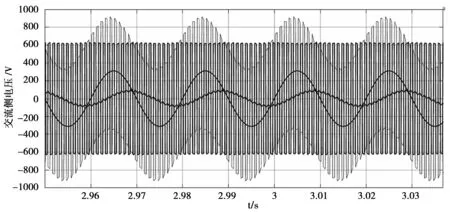
图6 单相VSR交流侧电压波形

4 结 论

单相全桥PWM整流器相位与幅值控制系统，能够将直流电压长期稳定在目标值附近，稳态条件下电压波动较小；可以实现网侧电流的正弦化，由于控制模型是依据VSR交流侧各电压相量静态数学关系建立的，网侧电流的动态变化没有直接体现在控制结构中，所以系统对电流相位的控制效果微弱。