解线性方程组最小二乘解的迭代法

张光辉

宿州学院数学与统计学院,宿州,234000

1 引 言

在技术和工程实践中，最小二乘问题应用非常广泛。所谓最小二乘问题[1]，是指针对线性方程组AX=b，寻找X*∈Rn，使得

(1)

其中A为一m×n矩阵，b为一m维给定向量。

2 引理及主要结果

引理1[2]设A∈Rm×n(m>n),b∈Rm，求解最小二乘问题AX=b，等价于极小化φ(X)=(AX-b,AX-b)。

ATAX=ATb

(2)

的解。

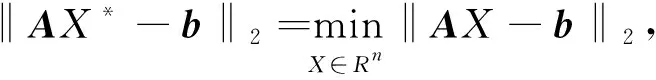
注：引理1,2从理论上说明求解最小二乘问题(1)只需求解方程(2)，但当ATA奇异，或对计算过程中不可避免的舍入误差十分敏感时，该方法在数值上是不可取的。应用引理3求A+时需要对A进行奇异值分解。但对于大规模的问题，直接采用奇异值分解十分困难，必须采用迭代法。下面给出三种具体的迭代算法。

算法1基于显示式欧拉算法[5]建立的迭代法

step1根据AX=b，给出φ(X)=(AX-b,AX-b)表达式；

step2计算φ(X)=(AX-b,AX-b)的负梯度方向-gradφ(X)=-AT(AX-b)；

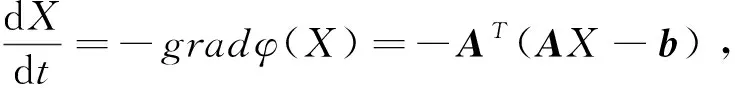
step4用显示式欧拉法求解step3微分方程，得到

Xk+1=Xk-hkAT(AXk-b)

并给定算法迭代允许误差ε；

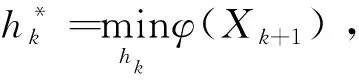
(3)

其中

step6如果φ(Xk+1)<ε或者‖Xk+1-Xk‖<ε，则算法迭代终止；否则将Xk+1赋给Xk，转step4继续迭代。

算法2二阶Runge-Kutta算法建立的迭代法

step1-step3同算法1；

step4用二阶Runge-Kutta算法求step3微分方程，得到

并给定算法迭代允许误差ε；

step5计算φ(Xk+1)，得到关于hk的四次多项式；

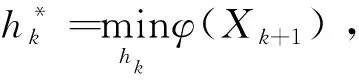
整理得到

(4)

step7如果φ(Xk+1)<ε或者‖Xk+1-Xk‖<ε，则算法迭代终止；否则将Xk+1赋给Xk，转step4继续迭代。

算法3基于隐式欧拉算法建立的迭代法

step1-step3同算法1；

step4用隐式欧拉法求step3微分方程，得到

Xk+1=Xk-hkAT(AXk+1-b)

将上式显化，得

并给定算法迭代允许误差ε；

step5计算φ(Xk+1)，得到关于hk的四次多项式；

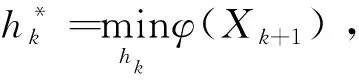
整理得到

(5)

step7如果φ(Xk+1)<ε或者‖Xk+1-Xk‖<ε，则算法迭代终止；否则将Xk+1赋给Xk，转step4继续迭代。

3 算例分析

算例1某种合金的含铅量百分比为P，其溶解温度为θ，由实验测得P与θ的数据见表1。

表1 合金含铅百分比与溶剂温度数据表

试用最小二乘法建立含铅量百分比P与溶解温度θ之间的经验公式θ=x1p+x2。用算法1,2,3计算，变量的允许误差ε=0.000 05。

解由题意，所求经验公式的待定参数(x1,x2)即为线性方程组AX=b的最小二乘解向量，其中

矩阵A的条件数cond(A)=249.79，秩rank(A)=2，由引理3广义逆矩阵结论得最小二乘解为X*=A+b=(2.233 7,95.352 4)T。现在用算法1进行迭代运算，验证算法的有效性。取(x1,x2)初始值为(1,1)，用Marlab软件编写程序代码，迭代7次便可得到具有五位有效数字的解，迭代结果如表2所示。

表2 算法1迭代解数据

由算法2进行迭代运算，取(x1,x2)初始值为(2,97)，迭代结果如表3所示。

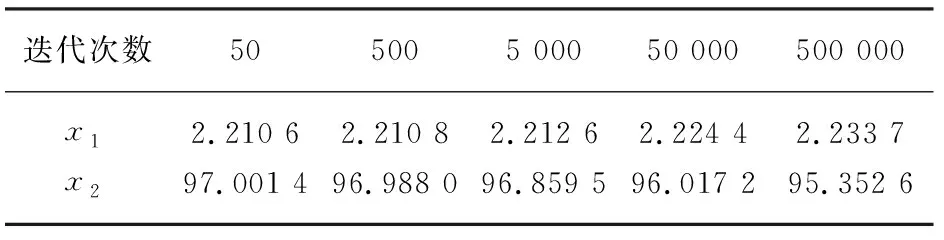
表3 算法2迭代解数据

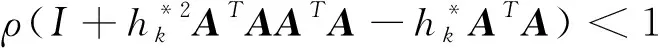
算例2求下面线性方程组的最小二乘解。

分析算法1,2，3的误差向量范数随迭代次数的变化情况。

解矩阵A的条件数cond(A)=2.5，秩rank(A)=3。

由引理2 所给方程组的最小二乘解即为ATAX=ATb的解

X*=(ATA)-1ATb

=(-0.801 9,-2.487 2,-3.415 1)T

用算法1,2,3分别进行迭代计算，用Matlab编程计算，得到迭代10次、50次、100次的误差，结果见表4。

表4 算法1,2,3迭代结果的误差向量范数

算例2表明，当系数矩阵为良态时，迭代矩阵的谱半径为影响迭代速度的主要因素，随着谱半径的减小，收敛速度加快，误差逐渐变小。

算例3求下面线性方程组的最小二乘解。

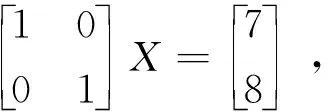
解为更好地对比三种算法的迭代效果，选取如上简单模型方程。矩阵A的条件数cond(A)=1，秩rank(A)=2。系数矩阵为非奇异方阵时，方程组的最小二乘解即为精确解，显然X*=(7,8)T。用三种算法进行迭代求解，结果见表5。

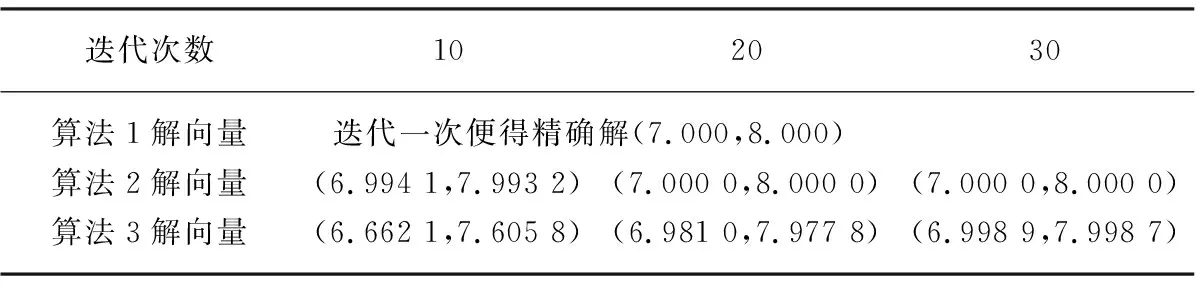
表5 算法1,2,3对算例3的迭代结果

算例3表明，当系数矩阵条件数不大，且迭代矩阵的谱半径小于1时，三种算法的迭代速度均有明显提高，收敛效果很好，且迭代矩阵的谱半径的大小依然是影响收敛效果的主要因素。

4 结 语

由于显式欧拉法、隐式欧拉法、二阶龙格-库塔算法是求常微分方程数值解非常经典的算法，且原理和公式相对简单，所以本文分析了基于以上三种数值解法建立的三种迭代法的迭代效果，结果表明，这三种算法的迭代效果与系数矩阵的是否病态，即矩阵的条件数有很大的关系。随着条件数减小到良态数值时，三种迭代法的迭代速度均有所加快，但速度不同，受迭代矩阵的谱半径的大小影响。同时，通过对3个算例的计算，表明文中所建立的三种算法在方程组的最小二乘解的求解过程应用中的适应性和有效性。算法1对问题的条件数适应性较强，要求不高，算法2,3 更适应于良态问题，对高条件数的问题效果不理想，当条件数相当时，算法2，3相比较而言，算法2精度稍高于算法3。